les parallelogrammes particuliers

O
ABCD est un parallélogramme
D C
BA
?
?
?
?
30°
4 cm
6 cm
O
DC
BA
Chapitre : Les parallélogrammes particuliers
I Les rectangles
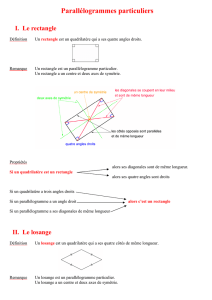
Définition des rectangles : Un rectangle est un quadrilatère qui a ses angles droits.
Propriétés des rectangles : Un rectangle a : – ses angles droits
– ses côtés opposés parallèles
– ses côtés opposés de la même longueur
– ses diagonales se coupent en leur milieu
– ses diagonales de même longueur.
ABCD est un rectangle
CD = 6 cm car les côtés opposés du rectangle ABCD ont la même longueur
AO = 4 cm car les diagonales du rectangle ABCD se coupent en leur milieu
☺
ADO = 90 – 30 = 60° car le rectangle ABCD a ses angles droits
BO = 4 cm car les diagonales du rectangle ABCD se coupent en leur milieu et ont la même longueur
Propriétés de reconnaissances des rectangles :
Un quadrilatère est un rectangle : – si il a trois angles droits
– si c’est un parallélogramme qui a un angle droit
– si c’est un parallélogramme qui a ses diagonales de même longueur.
ABCD est un rectangle car :
–
il a trois angles droits
–
c’est un parallélogramme qui a un angle droit an A
–
c’est un parallélogramme qui a ses diagonales de même longueur.

D
B
C
A
II Les losanges
Définition des losanges : Un losange est un quadrilatère qui a ses côtés de même longueur.
Propriétés des losanges : Un losange a : – ses côtés de même longueur
– ses côtés opposés parallèles
– ses diagonales qui se coupent en leur milieu
– ses angles opposés de la même mesure
– ses angles consécutifs supplémentaires
– ses diagonales perpendiculaires
– ses diagonales qui sont des bissectrices de ses angles
ABCD est un losange
Propriété de reconnaissance des losanges :
Un quadrilatère est un losange si : – ses côtés ont la même longueur
– c’est un parallélogramme qui a deux côtés consécutifs le même longueur
– c’est un parallélogramme qui a ses diagonales perpendiculaires.
III Les carrés
Un carré est à la fois un rectangle et un losange.
Propriété des carrés : Un carré a : – ses côtés de la même longueur
– ses côtés opposés parallèles
– ses diagonales qui se coupent en leur milieu
– ses diagonales de même longueur
– ses diagonales perpendiculaires
– ses angles droits
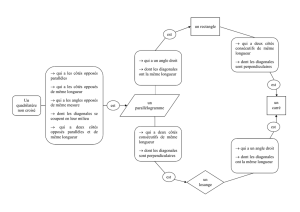
IV Tableau récapitulatif
PARALLÉLOGRAMME
RECTANGLE
LOSANGE
CARRÉ
Avec les diagonales
de même longueur
Avec les diagonales
perpendiculaires
Avec deux côtés consécutifs
de même longueur
Avec un angle droit
Avec les diagonales
de même longueur
Avec un angle droit
Avec les diagonales
perpendiculaires
Avec deux côtés consécutifs
de même longueur

D C
BA
D C
BA
D C
BA
2,5 cm
4 cm
74°
I
DC
BA
2 cm
3,6 cm
56°
I
D
C
B
A
O
D C
BA
H
F
G
E
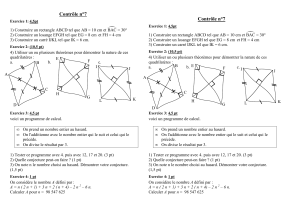
Exercice 1 :
a ) Sur la figure de droite, ABCD est un rectangle.
Trouve en expliquant : BD ; AC ; nature de IBC ; ☺ ICB ; ☺ BCD ; ☺ ICD ; AB.
b ) IJKL est un rectangle de centre O tel que IK = 5,8 cm ; IL = 3 cm et ☺ OIJ = 30°
Trouve en expliquant : ☺ JIL ; JK ; JL ; ☺ KIL ; nature de JOI ;☺ IOJ .
Exercice 2 :
a )
Quelle est la nature de ABCD ?
Justifie ta réponse.
b )
Quelle est la nature de ABCD ?
Justifie ta réponse.
c )
Prouve que AD = BC.
Exercice 3 : Construction.
a ) Sans utiliser le quadrillage, trace un triangle ABC rectangle en B puis, en n’utilisant que l’équerre, place le
point D tel que ABCD soit un rectangle. Explique pourquoi ABCD est bien un rectangle.
b ) Sans utiliser le quadrillage, trace un triangle EFG rectangle en F puis, en n’utilisant que la règle et le compas,
place le point H tel que EFGH soit un rectangle. Explique pourquoi EFGH est bien un rectangle.
c ) Trace un cercle de diamètre [IK] et de centre O et place un point J sur ce cercle.
En utilisant maintenant que ta règle, place le point L de façon à ce que IJKL soit un rectangle.
Explique pourquoi IJKL est bien un rectangle.
Exercice 4 : a ) Sur la figure de droite, ABCD est un losange.
Trouve en expliquant : ☺ AID ; BC ; ☺ ADC ; BD ; ☺ DAC ; ☺ ABC.
b ) IJKL est un losange de centre O tel que JL = 6 cm ; LK = 5 cm et ☺ IJK = 106°
Trouve en expliquant : ☺ ILK ; IL ;☺ JOI ; OJ ;☺ ILO ; nature de JIK ;☺ JIK .
Activité 1 : 1° ) Prouve qu’un parallélogramme qui a deux côtés consécutifs de même
longueur est un losange.
2° ) Construis un parallélogramme ABCD dont les diagonales sont perpendiculaires.
a ) Prouve que ( AC ) est la médiatrice du segment [BD].
b ) En déduire que : AB = AD.
c ) Conclure que ABCD est un losange.
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
Exercices pour préparer le contrôle
Exercices du livre : Exercices 6 et 7 P 230
Exercice 1 : Construis un triangle ABC rectangle en B, puis, en n’utilisant que la règle et le compas, place le point
D tel que ABCD soit un rectangle.
Exercice 2 : a ) ABCD est un rectangle de centre O tel que : BC = 6 cm et BD = 10 cm et ☺ AOB= 106°.
Trouve en expliquant pourquoi : AD ; BO ; AC ; ☺ BOC ; ☺ BAD.
b ) EFGH est un losange de centre O tel que : EG = 7,2 cm et HG = 5 cm et ☺ FEH = 88°.
Trouve en expliquant pourquoi : OE ; EH ;☺ FEG ; ☺ FGH ; ☺ EOH.
Exercice 3 :
a ) Donne toutes les raisons qui font que le
quadrilatère ABCD ci-dessous est un rectangle.
b ) Donne toutes les raisons qui font que le quadrilatère
EFGH ci-dessous est un losange.

Résultats des exercices pour préparer le contrôle
Exercices 6 P 230 : On trace les diagonales [LS] et [AO] perpendiculaires et qui se coupent en leur milieu.
Exercices 7 P 230 : On trace le triangle ESF rectangle en S puis on trace les points G et H symétriques de E et F
par rapport au centre S.
Exercice 1 : On trace deux arcs de cercle pour faire le parallélogramme ABCD.
Exercice 2 : a ) ABCD est un rectangle de centre O tel que : BC = 6 cm et BD = 10 cm et ☺ AOB= 106°.
Trouve en expliquant pourquoi :
AD = BC = 6 cm car les côtés opposés du rectangle ABCD ont la même longueur.
BO = 10
2 = 5 cm car les diagonales du rectangle ABCD se coupent en leur milieu.
AC = BD = 10 cm car les diagonales du rectangle ABCD ont la même longueur.
☺
BOC = 180 – 106 = 74°
☺
BAD = 90° car les angles du rectangle ABCD sont droits.
b ) EFGH est un losange de centre O tel que : EG = 7,2 cm et HG = 5 cm et ☺ FEH = 88°.
OE = 7,2
2 = 3,6 cm car les diagonales du losange EFGH se coupent en leur milieu.
EH = HG = 5 cm les côtés du losange EFGH ont la même longueur.
☺
FEG= 88 : 2 = 44° car les diagonales du losange EFGH sont des bissectrices de ses angles.
☺
FGH = ☺ FEH = 88° car les angles opposés du losange EFGH ont la même mesure.
☺
EOH = 90° car les diagonales du losange EFGH sont perpendiculaires.
Exercice 3 :
a ) ABCD est un parallélogramme car ses
diagonales se coupent en leur milieu.
ABCD est un rectangle car :
1° ) il a trois angles droits.
2° ) c’est un parallélogramme qui a un angle droit.
3° ) c’est un parallélogramme qui a ses diagonales
de même longueur.
b ) EFGH est un parallélogramme car c’est un quadrilatère
non croisé qui a ses côtés opposés de la même longueur.
EFGH est un losange car :
1° ) ses côtés ont la même longueur.
2° ) c’est un parallélogramme qui a ses diagonales
perpendiculaires.
3° ) c’est un parallélogramme qui a ses côtés consécutifs
[EF] et [FG] de même longueur.