Correction devoir surveillé n°7 – 2nde Exercice 1 : (5 points) On

Correction devoir surveillé n°7  2nde
Exercice 1 : (5 points)
On lance deux dés cubiques équilibrés numérotés de 1 à 6 est le plus
grand des deux numéros sortis.
1. 
1
2
3
4
5
6
Ainsi on obtient la loi de probabilité suivante:
1
2
3
4
5
6
1
1
2
3
4
5
6
2
2
2
3
4
5
6
3
3
3
3
4
5
6
4
4
4
4
4
5
6
5
5
5
5
5
5
6
6
6
6
6
6
6
6
2. Compléter ci-contre représentant
cette expérience aléatoire.
Exercice 2 : (6,5 points)
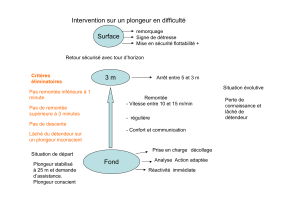
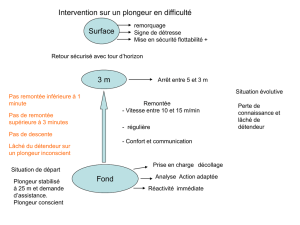
temps écoulé, en secondes, depuis le départ du plongeur par :     
1.   
2.  est le temps en secondes écoulé depuis que le plongeur a sauté donc   .
3.  est une fonction trinôme du second degré avec   ,   
 et    .
Sa représentation graphique est une parabole. Comme    alors la parabole est tournée vers le
bas et la fonction  est croissante sur 
 puis décroissante sur   . Enfin son sommet a
pour coordonnées 
Ainsi le tableau de variation de la fonction  est :
Variation de 
4
4.   .
          . Le plongeoir se trouve donc à 3 mètres de haut.
5. es 
.
6.  
  ou      par la règle du produit nul.
 ou   
Or   
Variables : D1 et D2 nombres entiers
Début
Si   
alors afficher D1
Sinon afficher D2
Fin Si
Fin

Exercice 3 : (5 points)
D'après la représentation graphique suivantes nous pouvons dire que :
  fonction linéaire; sa représentation graphique est une droite passant par l'origine.
    fonction affine; sa représentation graphique est une droite
a.            - VRAI
b.            - VRAI
c.        - FAUX
Contre-exemple : pour         
d.                - VRAI
e.           - FAUX
Contre-exemple : pour           
f.            - FAUX
Contre-exemple :          
g.         - VRAI
Exercice 4 : (3,5 points)
Lilou veut visiter trois capitales européennes : Prague (P) ; Vienne (V) et Budapest (B)
1.
Lilou
P
V
B
B
V
V
P
B
B
P
B
P
V
V
P
Nous en déduisons que 6 chemins sont possibles : PVB; PBV; VPB; VBP; BPV; BVP.
2. a. On obtient alors que Lilou a une probabilité de 
 soit   de terminer son circuit à Vienne.
(2 chemins sur les 6)
b. On obtient alors que Lilou a une probabilité de 
 soit   de visiter Vienne avant Prague.
(3 chemins sur les 6)
Bonus : Marc a laissé couler son stylo sur sa copie.
La fonction représentée est    
Peut-il quand même répondre à la question suivante :
La fonction f admet-elle un extremum ?
Si oui, donné sa valeur et en quel point est-il atteint.
    est la forme développé d'un trinôme du seconde degré.
Elle admet donc un extremum que l'on notera atteint pour   .
De plus, on sait que sa représentation graphique est une parabole symétrique
par rapport à la droite parallèle à l'axe des ordonnée et passant par .
Ainsi d'après la représentation graphique donnée on en déduit que   .
Ainsi f admet un minimum valant             et donc atteint pour  
En plus:
Forme canonique de sommet de coordonnées .