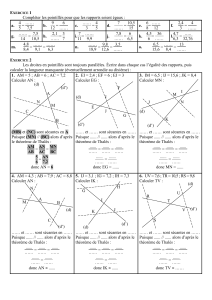
Théorème de Thalès

ThéorèmedeThalès.Projectiondansleplanetdansl’espace,
caractèrea¢nedesprojections.
Dany-JackMercier
IUFMdeGuadeloupe,MorneFerret,
BP399,Pointe-à-Pitrecedex97159,France
[e-mail]
23juin2003
Onsupposeconnuslesaxiomesd’unespacevectorieletceuxd’unespacea¢neainsiquedes
rudimentsdecalculvectoriel.LeThéorèmedeThalèsestunrésultata¢nequidoitêtreprésenté
dansuncadrea¢ne,c’est-à-diresansfaireintervenirunedistance.Lecadrea¢nesu¢tpour
introduirelanotiondemesurealgébriquesurunedroitedonnée:si Aet Bsontdeuxpoints
d’unedroite Ddevecteurdirecteur ¡!i,lamesurealgébriqueducouple (A;B)(associéeauchoix
duvecteur ¡!i)est,pardé…nition,l’abscisse xduvecteur ¡! AB danslabase ¡!ide ¡! D.Autrement
ditc’estleréel xtelque ¡! AB =x¡!i,etl’onpose AB =x.
1ThéorèmedeThalèsdansleplan
Théorème1-ThéorèmedeThalèsdansletriangle.
Soientdeuxtrianglesnonaplatis OAA0et OBB0tels
que A2(OB)et A02(OB0).Si (AA0)estparallèle
à(BB0),alors OA
OB =OA0
OB0=AA0 BB0:
OO
AA
A'
BB
B'
Preuve:Ceségalitésproviennentdesaxiomesd’espacea¢neetdeceuxd’espacevectoriel.
Ene¤et,direque (AA0)estparallèleà(BB0)signi…equ’ilexiste k2Rtelque ¡¡! BB0=k¡¡! AA0.
Parhypothèse,ilexistedeuxréels ®;®
0telsque ¡!
OB =®¡! OA et ¡¡! OB0=®0¡¡! OA0,donc
¡¡!
BB0=k¡¡! AA0)¡¡! OB0¡¡! OB =k³¡¡! OA0¡¡! OA´)®0¡¡! OA0¡®¡! OA =k¡¡! OA0¡k¡! OA:
Celaentraîne ®=®0=kpuisquelesvecteurs ¡! OA et ¡¡! OA0sontlinéairementindépendants.Ainsi
¡!
OB =k¡! OA,¡¡! OB0=k¡¡! OA0et ¡¡! BB0=k¡¡! AA0fournissentleségalitésannoncées(bienentendu,les
mesuresalgébriquessurlesdroitesparallèles (AA0)et (BB0)sontassociéesauchoixd’unmême
vecteurdirecteurdeladirection R¡¡! AA0communeàcesdeuxdroites).
0[ctht0001]v1.11http://perso.wanadoo.fr/megamaths
c
°2003,D.-J.Mercier.Vouspouvezfaireunecopiedecesnotespourvotreusagepersonnel.
1

Théorème2-ThéorèmedeThalès.
Soient Det D0deuxdroitesdistinctes,et A;B;C (resp. A0;B0 ;C0 )troispointsdistinctsappar-
tenantàD(resp. D0)avec A6=A0,B6=B0,C6=C0.Silesdroites (AA0),(BB0),(CC0)sont
parallèles,alors AB
AC =A0B0
A0C0.
ABC
A'
B' C'
ABC
A'
B' C'
D'
DD
D'
BC1
1
O
Preuve: ²Si Det D0sontparallèles,lesquadrilatères AA0B0Bet AA0C0Csontdesparal-
lélogrammes,donc ¡¡! A 0B0=¡! AB et ¡¡! A 0C0=¡! AC.Celaentraînebien A0B0=AB et A0C0=AC et
l’égalitédesquotients.Nousavonsseulementutilisélerésultat:
(AB)== ¡A0B0¢et ¡AA0¢== ¡BB0¢)¡¡! A 0B0=¡! AB et ¡¡! AA0=¡¡! BB0:
Montrons-le(laréciproqueesttrivialeetnousfournitlacaractérisationvectorielledesparal-
lélogrammes).Parhypothèse,ilexistedeuxréels ket stelsque ¡¡! A 0B0=k¡! AB et ¡¡! AA0=s¡¡! BB0.
Comme ³¡! AB; ¡¡! BB0´estunebase,leségalités
¡¡!
AB0=¡! AB +¡¡! BB0=¡¡! AA0+¡¡! A 0B0=s ¡¡! BB0+k¡! AB
entraînent k=s=1etlaconclusion.
²Si Det D0secoupenten O,leThéorème1entraîne
OA
OA0=OB OB0=OB ¡OA OB0¡OA0=AB A0B0:
Demême OA
OA0=AC A0C0etl’ondéduitbien AB A0B0=AC A0C0.Uneautresolutionconsisteàtracer
laparallèleà(A
0
B
0
)passantpar A.Cetteparallèlecoupe (BB0)en B1et (CC0)en C1,etle
Théorème1entraîne AB
AC =AB1 AC1=A0B0
A0C0sil’onutiliselapremièrepartiedelapreuve.
Théorème3-RéciproqueduThéorèmedeThalès.
Soient Det D0deuxdroitesdistinctes,et A;B;C (resp. A0;B
0
;C0 )troispointsdistinctsap-
partenantàD(resp. D0)avec A6=A0,B6=B0,C6=C0.Si (AA0)estparallèleà(BB0)etsi
AB
AC =A0B0
A0C0alorslesdroites (AA0),(BB0),(CC0)sontparallèles.
Preuve:Onutiliselesensdirecte.Soit C00 l’intersectiondeladroite (AB)etdelaparallèle
à(AA0)passantpar C.LeThéorèmedeThalèsentraîne AB
AC =A0B0
A0C00 ,etcomme AB
AC =A0B0
A0C0par
hypothèse,ondéduit A0B0
A0C00 =A0B0 A0C0,soit A0C00 =A0C0puis C00 =C0.
2

Remarque :L’hypothèse”(AA0)
estparallèleà(BB0)”estprimordiale
danslaréciproqueduThéorèmede
Thalès,commelemontreledessin
ci-contrepourlequellesrapports
sontégauxsansquelesdroites
soientparallèles.
AA BB
CC
A' B'
C'
11
22
22
11
2Projectionsdansleplan
Dé…nition1Soient Det ¢deuxdroitessécantesduplana¢ne P.Laprojectionsur D
parallèlementà¢estl’application pde Pdans Pquiaupoint Mde Passocielepoint M0de
¢telque (MM0)soitparallèleà¢.
Untelpoint M0existeetestuniquepuisquelesdroites Det ¢n’ontpaslamêmedirection.
Théorème4-Caractèrea¢nedesprojections(Casduplan).
L’application p:P!P esta¢ne.Autrementditsi ¡! PdésigneleplanvectorielassociéàP,
l’application
¼:¡! P¡! ¡! P
¡!
u=¡¡! MN 7¡! ¡¡¡! M0N0où M0=p(M)et N0=p(N)
estlinéaire.
Preuve :Onmontreque ¼estbiendé…nietque ¼³¡¡! MN +¡! PQ
´=¼³¡¡!
MN´+¼³¡! PQ
´comme
auThéorème5quiseraénoncéendimension…niequelconque.Lorsquenoustravaillonsdans
unplan,nouspouvonsdéduireleségalitésdutype ¼³¸¡¡! MN´=¸¼ ³¡¡! MN´duThéorèmede
Thalès.Ene¤etsi ¸2R¤posons ¸¡¡! MN =¡! RS etprimonslesimagespar p.Si (MN)==¢ousi
M=N,alors ¡¡¡! M0N0=¡¡! R0S0=¡! 0etl’égalité ¡¡! R0S0=¸ ¡¡¡! M0N0esttriviale.SinonleThéorèmede
Thalèspermetd’écrire
¸=RS
MN =R0S0
M0N0)¡¡!
R0S0=¸ ¡¡¡! M0N0)¼³¸ ¡¡! MN´=¸¼ ³¡¡! MN´:
3Projections(casgénéral)
Dansceparagraphe Ereprésenteunespacea¢nededirectionunespacevectorieldedimension
…nie ¡! E.Si ¡! Festunsous-espacevectorielde ¡! E,onnote F=A+¡! Flesous-espacea¢ne
passantpar Adedirection ¡! F.C’estl’ensemble
F=A+¡! F=n M2E=¡¡! AM 2¡! Fo:
3

Onrappellequedeuxsous-espacesvectoriels ¡! Fet ¡! Gsontsupplémentairesdans ¡! Esitout
vecteur ¡! ude ¡! Es’écritdemanièreuniquesouslaforme ¡! u=¡! v+¡! wavec ¡! v2¡! Fet ¡! w2¡! G.
Danscecas,onnote ¡! E=¡! F©¡! G.Celaéquivautàdireque ¡! F\¡! G=© ¡! 0ªet ¡! E=¡! F+¡! G
(cedernierpointsigni…equetoutvecteur ¡! ude ¡! Es’écritsouslaforme ¡! u=¡! v+¡! wavec
¡!
v2¡! Fet ¡! w2¡! G).
Lemme1Si Fet Gsontdeuxsous-espacesa¢nesdedirections ¡! Fet ¡! Gsupplémentaires
dans ¡! E,alors F\Gestunsingleton.
Preuve:Notons F=A+¡! Fet G=B+¡! G.Ona
M2F\G,¡¡! AM 2¡! Fet ¡¡! BM 2¡! G)¡! AB =¡¡! AM +¡¡! MB 2¡! F+¡! G:
Parhypothèse,levecteur ¡! AB sedécomposedemanièreuniquesouslaforme ¡! AB =¡! v+¡! w
avec ¡! v2¡! Fet ¡! w2¡! G,donc
M2F\G)¡! AB =¡¡! AM +¡¡! MB =¡! v+¡! w)¡¡! AM =¡! v
etl’unicitéde M2F\Gestassurée.Réciproquement,lepoint Mdé…nipar ¡¡! AM =¡! v
appartientbienàF,et ¡! AB =¡! v+¡! w=¡¡! AM +¡! wentraîne ¡¡! MB =¡! w2¡! Gsoit M2G.Ona
montréque M2F\G.
Dé…nition2Soient Fet Gdeuxsous-espacesa¢nesdedirections ¡! Fet ¡! Gsupplémentaires
dans ¡! E.Laprojectionsur Fparallèlementà¡! G(ouàG)estl’application
p:E¡! E
M7 ¡! M0telque F\³M+¡! G´=f M0g:
Remarque:L’imaged’unpointparlaprojection p
estcaractériséepar:
M
0=p(M),½M
02F
¡¡¡!
MM02¡! G:
Ilsu¢tdetraduirecesystèmeenutilisantles
coordonnéesde Metde M0pourobtenirla
représentationanalytiquede pdansunrepèredonné.
M'
N
M
N'
G
F
Théorème5-Caractèrea¢nedesprojections.
Laprojection p:E!Esur FparallèlementàGestuneapplicationa¢ne,autrementdit
l’application
¼:¡! E¡! ¡! E
¡!
u=¡¡! MN 7¡! ¡¡¡! M0N0où M0=p(M)et N0=p(N)
estlinéaire.
4

Preuve :L’application ¼estbiendé…nicar ¼(¡! u)nedépendpasduchoixde M;N telsque
¡!
u=¡¡! MN.Ene¤et,si ¡! u=¡¡! MN =¡! PQ etenprimanttoujourslesimagespar p,onobtient
¡¡¡!
M0N0+³¡¡¡! MM0+¡¡! N0N´=¡¡! P0Q 0+³¡¡! PP0+¡¡! Q 0Q ´;
etl’unicitédeladécompositiond’unvecteurdanslasommedirecte ¡! F©¡! Gentraîne ¡¡¡! M0N0=
¡¡!
P0Q 0.
Montronsmaintenantque ¼estlinéaire.Si ¸2Retsi M;N;P;Q 2Esontdonnés,onpeut
trouverdeuxpoints Ret Stelsque ¸¡¡! MN +¡! PQ =¡! RS.Ona
¸
¡¡¡!
M0N0+¡¡! P0Q 0+¸³¡¡¡! MM0+¡¡! N0N´+³¡¡! PP0+¡¡! Q 0Q ´=¡¡! R0S0+³¡¡! RR0+¡! S0S´
d’où ¸¡¡¡! M0N0+¡¡! P0Q 0=¡¡! R0S0d’aprèsl’unicitédeladécompositiond’unvecteurdans ¡! F©¡! G.Cela
s’écritencore ¼³¸¡¡! MN +¡! PQ
´=¸¼ ³¡¡!
MN´+¼³¡! PQ
´etachèvelapreuveduThéorème.
Remarques:1)Onpeutcourt-circuiterlapreuvedelalinéaritéde ¼dansladémonstration
ci-dessusenétudiantd’abordlesprojectionsvectorielle.Si ¡! Fet ¡! Gsontdeuxsous-espaces
vectorielssupplémentairesdans ¡! E,onappelleprojectionvectoriellesur ¡! Fparallélementà¡! G
l’application pr:¡! E!¡! Equiàtoutvecteur ¡! usedécomposanten ¡! u=¡! v+¡! w,¡! v2¡! F,
¡!
w2¡! G,associelevecteur pr(
¡!
u)=¡! v.Onvéri…eaisémentqu’unetelleapplicationest
linéaire.Ladécomposition
¡¡!
MN =¡¡¡! M0N0+³¡¡¡! MM0+¡¡! N0N´où ¡¡¡! M0N02¡! Fet ³¡¡¡! MM0+¡¡! N0N´2¡! G
montreque pr ³¡¡! MN´=¡¡¡! M0N0pourtouspoints Met N,d’où ¼=pr.
2)Ildevientinutiledevéri…erquel’application ¼duThéorème5estbiendé…niesionla
dé…nitenposant:
¼:¡! E¡! ¡! E
¡!
u=¡¡! OM 7¡! ¡¡¡! O0M0où M0=p(M)et O0=p(O)
où Odésigneunpointquelconque…xéàl’avance.Danscecastoutvecteur ¡! udé…nitununique
point Mtelque ¡! u=¡¡! OM etl’image ¼(¡! u)estparfaitementdéterminéepar M.
Exemples: Misàpartlesprojectionssur Eousur ©¡! 0ªquio¤rentpeud’intérêt,lesseules
projectionsdansunespacededimension 2ou 3seront
-lesprojectionssurunedroiteparallèlementàunedroite,dansleplan,
-lesprojectionssurunedroiteparallèlementàunplan,dansl’espacededimension 3,
-lesprojectionssurunplanparallèlementàunedroite,dansl’espacededimension 3.
M
M'
M
M'
M
M'
5