lunette ou télescope - Lycée Hilaire de Chardonnet

LUNETTE OU TÉLESCOPE ?
1. Une lunette astronomique.
1.1.1. Le diamètre apparent α de l'objet est l’angle sous lequel on observe l’objet à l'œil nu.
1.1.2.
tan 2
α
= /2D
d = 2
D
d
Comme α est petit et exprimé en radian,
alors tan α = α
2
α
= 2
D
d
D = d.α
D = 9,3×10–3 × 3,8 × 105
D = 3,5×103 km diamètre réel de la Lune.
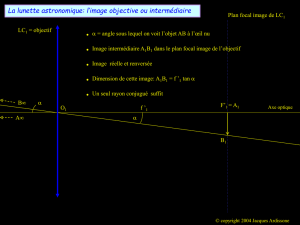
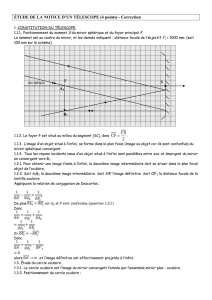
1.2.1. L'objet AB est à l'infini ( 1 OA=−∞), donc l'image A1B1 se forme dans le plan focal image de
l'objectif L1. En effet d'après la relation de conjugaison de Descartes:
11
1
OA −
1
1
OA =
11
1
'OF ,
soit 11 11
'OA OF=. Le point A1 est confondu avec le foyer principal image F'1.
On prolonge le rayon issu de B et passant par O1 , ce rayon n'est pas dévié.
Le point image B1 est situé à l'intersection du plan focal image avec ce rayon.
1.2.2. tan α = 11
11
'
AB
OF α étant petit et exprimé en radian, alors tan α = α.
α = 11
11
'
AB
OF donc A1B1 = α .O1F1' A1B1 = α . f1'
A1B1 = 9,3×10–3 × 100 = 9,3×10–1 cm
1.3.1. A1B1 doit être située dans le plan focal objet de l'oculaire L2 , ainsi l'image définitive A'B' est
rejetée à l'infini.
1.3.2. On place F2 confondu avec A1 et F2' symétrique de F2 par rapport à la lentille L2. Voir figure ci-
dessus.
1.3.3. Construction de l'image définitive A'B': voir figure ci-dessus.
On trace un rayon issu de B1 passant par O2, il émerge sans être dévié.
On trace un rayon issu de B1 et parallèle à l'axe optique, il émerge en passant par F2'.
A' et B' sont rejetés à l'infini.
1.4.1. Dans le triangle O2A1B1 rectangle en A1:
tan α' = 11
22
AB
OF = 11
2
AB
f
α' petit et exprimé en radian donc α' = 11
2
AB
f
α
d
=
3,8
×
1
0
5k
m
D
O2
L2
F'1
B1
A1
F2
F2'
B' ∞
α
'
L1
O1 α
B∞
A∞
O2
L2
F'1
B1
A1
F2
F
2
'
B' ∞
A' ∞

α' =
1
9, 3 10
10,0
−
× = 9,3 × 10–2 rad
1.4.2. G =
α
α
'
G =
2
3
9,3 10
9,3 10
−
−
×
× = 10
1.4.3. " Le grossissement d’une lunette est égal à la distance focale de l’objectif divisée par celle de
l’oculaire …"
G =
'
1
'
2
f
f
G = 100 10,0
10,0
= On obtient le même résultat qu'à la question précédente.
1.5.1. Le cercle oculaire d’une lunette est l’image du contour de l’objectif donnée par l’oculaire.
1.5.2. Construction du cercle oculaire :
1.5.3. On construit la projection du cercle oculaire sur l’oculaire (L2)
La propriété de Thalès s’écrit : C.Oc 2
Obj 1
ff
∅=
∅ donc C.Oc Obj 1
G
∅
=∅ ×
D’où : ∅C.Oc = 5.10-2 / 10 = 5.10-3 m, soit 5,0 mm.
1.5.4. Î Connaître la position du cercle oculaire permet de savoir où mettre son œil pour percevoir
l’image avec la meilleure luminosité possible. (Parfois le fabricant de l’oculaire place un tube muni d’un
embout caoutchouté qui permet de reposer son arcade sourcilière à la distance idéale permettant de mettre
la pupille de l’œil au cercle oculaire.)
Î Connaître le diamètre du cercle oculaire est un critère de qualité d’un instrument d’optique. Il est
nécessaire que ce diamètre soit inférieur à celui de la pupille pour que la totalité de la lumière collectée
par l’objectif soit reçue dans l’œil.
(Remarque : on considère ici une pupille dilatée puisqu’un lunette sert à observer les astres de nuit, soit
un diamètre d’environ 7 mm)
L1
O1
α
B∞
A∞
O2
L2
F'1
F'2
F2
Cercle
oculaire
L1
O1 α
B∞
A∞
O2
L2
F'1
F'2
F2
Cercle
oculaire
f1 f2

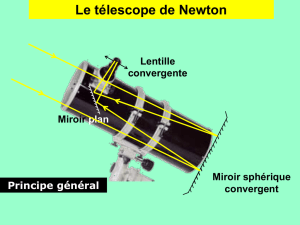
2. Un télescope.
2.1.1. Le miroir secondaire réfléchit la lumière vers l'oculaire. De l'image A1B1 donnée par le miroir
primaire, il donne une image A2B2.
2.1.2. La lumière issue de l'astre est renvoyée par le miroir primaire, à l'intérieur du tube du télescope.
Pour observer l'image A1B1 l'astronome devrait se mettre face au tube… Il empêcherait alors la lumière
d'entrer dans le tube du télescope. Le miroir secondaire permet de réfléchir la lumière issue de l'astre
suivant un axe perpendiculaire à l'axe optique du miroir primaire.
2.2.1. Construction de A2B2 : Cette image est symétrique de A1B1 par rapport au plan du miroir
secondaire.
A2 est confondu avec le foyer principal objet F2 de l'oculaire.
Construction de l'image définitive A'B':
- on trace un rayon issu de B2 et passant par O2 sans être dévié,
- on trace un rayon issu de B2 parallèle à l'axe optique, il émerge de l'oculaire en passant par F'2,
l'image A'B' est rejetée à l'infini.
2.2.2. Le rayon issu de B, frappe le miroir primaire en I. Il est réfléchi et se dirige vers B1.
Ce rayon frappe le miroir primaire, y est réfléchi et se dirige vers B2.
Le rayon traverse la lentille, et émerge parallèlement aux rayons précédents puisqu’il est lui aussi issu de B.
A2
B2
B' ∞
A' ∞