DROITES REMARQUABLES DU TRIANGLE

DROITES REMARQUABLES DU TRIANGLE
MEDIATRICES
Définition :
La médiatrice d’un segment est la droite passant par le milieu du segment en lui
étant perpendiculaire.
La médiatrice d’un segment est l’axe de symétrie du segment.
Propriété :
Si un point est sur la médiatrice d’un segment alors il est équidistant des
extrémités du segment.
Réciproquement :
Si un point est équidistant des extrémités d’un segment alors il est sur la
médiatrice de ce segment.
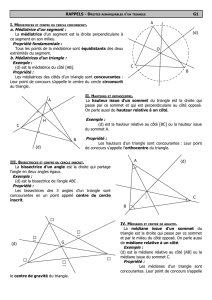
Médiatrices des côtés d’un triangle
Propriété :
Dans un triangle, les médiatrices des trois côtés sont concourantes en un point
qui est le centre du cercle circonscrit à ce triangle.
Le cercle circonscrit au triangle est le cercle passant par ses trois sommets.
BISSECTRICES
Définition :
La bissectrice d’un angle est la demi-droite partageant l’angle en deux angles
adjacents de même mesure.
La bissectrice d’un angle est l’axe de symétrie de l’angle.
Propriété :
Si un point est sur la bissectrice d’un angle alors il est équidistant des côtés de
l’angle.
Réciproquement :
Si un point est équidistant des côtés d’un angle alors il est sur la bissectrice de
cet angle.
a
KOH
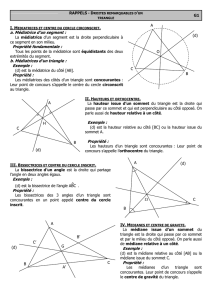
Bissectrices des angles d’un triangle
Propriété :
Dans un triangle, les bissectrices des trois angles sont concourantes en un point
qui est le centre du cercle inscrit à ce triangle.
Le cercle inscrit au triangle est le cercle tangent aux trois côtés du triangle.

DROITES REMARQUABLES DU TRIANGLE (suite)
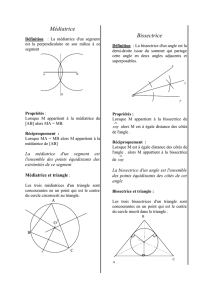
HAUTEURS D’UN TRIANGLE
Définition :
Une hauteur d’un triangle est la droite passant par un sommet et perpendiculaire
au côté opposé à ce sommet.
Propriété :
Dans un triangle, les trois hauteurs sont concourantes en un point appelé
MEDIANES D’UN TRIANGLE
Définition :
Une médiane d’un triangle est la droite passant par un sommet et le milieu du
côté opposé à ce sommet.
orthocentre.
Hauteur issue de A
Propriété :
Dans un triangle, les trois médianes sont concourantes en un point appelé centre
de gravité du triangle.
DROITES REMARQUABLES ET TRIANGLES PARTICULIERS
Triangle isocèle : Triangle équilatéral :
La hauteur, la médiane, la bissectrice issues du
sommet principal et la médiatrice du côté opposé à
ce sommet (la base du triangle) sont confondues.
La médiatrice de chaque côté est confondue avec la
hauteur, la médiane et la bissectrice issues du
sommet opposé.
Triangle rectangle :
Les médiatrices ont comme point d’intersection le
milieu de l’hypoténuse.
Le cas du triangle rectangle est étudié dans une
autre fiche : voir triangle rectangle et cercle
circonscrit.
Médiatrice du segment [AB]
Bissectrice de l’angle a ACB
Médiane et hauteur issues de C