Alan Turing et la résolution numérique des équations

CE QU’ALAN TURING NOUS A LAISS´ E 31
[5] K. G¨odel, ¨ Uber Eine Bischer Noch Ben¨utzte Erweiterung des Finiten Standpunktes, Dialec-
tica,12 (1958), 280-287. (On a hitherto unexploited extension of the finitary standpoint,
Journal of Philosophical Logic,9(1980) - English translation).
[6] A. Hodges, Alan Turing, the enigma, Vintage, (1988), London, UK
[7] T. Neary and D. Woods. Four small universal Turing machines. Fundamenta Informaticae,
91(1), (2009), 123-144
[8] P. Odifreddi, Classical recursion theory,125, Studies in Logic and the Foundations of Ma-
thematics, North-Holland Publishing Co., Amsterdam, (1989).
[9] H. Rogers, Theory of Recursive Functions and Effective Computability, (1967), McGraw-Hill ;
new edition : (1987), MIT Press
[10] A.M. Turing, On computable real numbers, with an application to the Entscheidungsproblem,
Proceedings of the London Mathematical Society, ser. 2, 42, 230-265, (1936).
[11] A.M. Turing, Systems of logic based on ordinals, Proceedings of the London Mathematical
Society, (1939), s2-45(1), 161-228
[12] A.M. Turing, Intelligent Machinery, National Physical Laboratory Report. In Meltzer, B.,
Michie, D. (eds), (1969), Machine Intelligence 5, Edinburgh : Edinburgh University Press, 3-
23.
Reproduced with the same pagination in :
Ince, D.C. (ed.), (1992), Collected Works of A.M. Turing : Mechanical Intelligence, Amster-
dam, North Holland
[13] A.M. Turing, Computing machinery and intelligence, Mind, (1950), 59, 433-460
[14] A.M. Turing, The Chemical Basis of Morphogenesis, Philosophical Transactions of the Royal
Society of London, Series B, Biological Sciences, (1952), 237(641), 37-72
[15] J. von Neumann, The general and logical theory of automata, dans Collected works, vol.5,
Design of computers, theory of automata and numerical analysis, (1963), Macmillan, 288-328
Alan Turing et la r´esolution num´erique
des ´equations diff´erentielles
Gilles Dowek
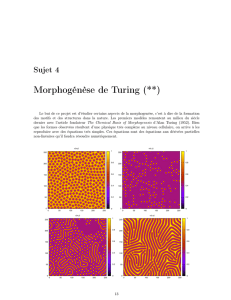
L’article The Chemical Basis of Morphogenesis, publi´e en 1952, tient une place
`a part dans l’œuvre d’Alan Turing : alors que, dans ses travaux ant´erieurs, il s’est
beaucoup int´eress´e `a des structures discr`etes, telles ses c´el`ebres machines, Tu-
ring d´ecrit, dans cet article, les processus de r´eaction-diffusion responsables de la
morphog´en`ese, en mod´elisant les concentrations des diff´erents r´eactifs avec des
fonctions `a valeur r´eelle, d´ependant d’un temps continu et d’un espace, soit discret
soit continu, ce qui le m`ene `a des syst`emes d’´equations diff´erentielles ordinaires
dans le premier cas et `a des ´equations aux d´eriv´ees partielles dans le second.
Mˆeme si le continu n’est pas totalement absent des travaux ant´erieurs de Tu-
ring – ainsi les machines de Turing sont motiv´ees, en 1936, par la volont´e de
d´efinir une notion, non de fonction calculable, mais de r´eel calculable – ce choix
peut surprendre : en mod´elisant les concentrations, le temps et l’espace de mani`ere
discr`ete, Turing aurait pu d´ecrire les ph´enom`enes morphog´en´etiques en utilisant
des automates cellulaires, d´efinis quelques ann´ees plus tˆot par Stanislaw Ulam et
John Von Neumann, et qui font rapidement ´emerger des formes complexes.
Mais, quelles qu’en soient les raisons, cette incursion de Turing dans l’analyse
lui a permis d’aborder – une fois de plus, en pionnier – une question qui refera
SMF – Gazette – 135, janvier 2013

32 G. DOWEK
surface `a la fin du XXesi`ecle : celle de la valeur des d´emonstrations effectu´ees
avec un ordinateur. Dans la treizi`eme et derni`ere partie de cet article, intitul´ee
«Non-linear theory. Use of digital computers », Turing constate, en effet, que les
´equations auxquelles il parvient peuvent ˆetre r´esolues explicitement, uniquement
quand la vitesse de r´eaction d´epend lin´eairement des concentrations, ce qui est
exceptionnel. Dans le cas g´en´eral, la r´esolution des ´equations est plus difficile et
Turing ´evoque la possibilit´e de r´esoudre ces ´equations en utilisant un ordinateur.
Bien entendu, cette id´ee de r´esolution num´erique des ´equations diff´erentielles n’´etait
pas enti`erement nouvelle, puisqu’elle avait ´et´e ´evoqu´ee deux si`ecles plus tˆot par
Euler dans son Institutionum calculi integralis, mais les ordinateurs, r´ecemment
apparus en 1952, donnent `a ces m´ethodes une applicabilit´e sans pr´ec´edents.
En comparant ainsi les r´esolutions exacte et num´erique des ´equations de
r´eaction-diffusion, Turing comprend d´ej`a beaucoup des avantages et inconv´enients
de la r´esolution num´erique. Du cˆot´e des avantages, qui selon Turing dominent, la
possibilit´e de traiter des cas beaucoup plus complexes. Turing ´evoque le cas non
lin´eaire, mais aussi la possibilit´e de prendre en compte la m´ecanique des syst`emes
mod´elis´es, de la mˆeme mani`ere qu’il prend en compte leur chimie. Du cˆot´e des
avantages ´egalement, la possibilit´e visualiser les solutions. De mˆeme que le ca-
ract`ere algorithmique du calcul int´egral avait donn´e des ailes aux math´ematiciens
de la fin du XVIIesi`ecle, qui avaient pu commencer `a ´etudier des courbes – la
chainette, la cyclo¨ıde, ... – trop complexes pour ˆetre abord´ees avec les ´epuisantes
m´ethodes archim´ediennes, la possibilit´e de calculer et repr´esenter les solutions
qu’offre la r´esolution num´erique donnera des ailes aux math´ematiciens de la
seconde moiti´e du XXesi`ecle, qui n’auront plus `a faire ce gigantesque effort
de visualisation des courbes et des surfaces. Mˆeme si, en 1952, les ordinateurs
n’offraient que des possibilit´es tr`es frustes de visualisation, Turing remarque d´ej`a
que, mˆeme dans le cas lin´eaire o`u le calcul exact des solutions est possible, le
traitement calculatoire a ´et´e «most illuminating ».
Mais, malgr´e son enthousiasme, Turing comprend aussi les limites de cette
d´emarche, qui permet de traiter des cas particuliers, mais non le cas g´en´eral. Pour
illustrer cette diff´erence, consid´erons par exemple l’´equation du mouvement, dans le
champ gravitationnel du Soleil, d’une com`ete dont nous connaissons la position et
la vitesse «initiales ». La r´esolution num´erique, pour quelques valeurs particuli`eres
des conditions initiales nous montrera des trajectoires parfois elliptiques, parfois
hyperboliques, mais elle ne nous donnera pas l’assurance que cette trajectoire est
`a coup sˆur une conique, ni une condition sur les conditions initiales qui nous in-
dique quand cette trajectoire est une ellipse, une parabole ou une hyperbole. En
d’autres termes, mˆeme pour un cas particulier, la r´esolution num´erique nous dit
que la trajectoire est telle ou telle, mais elle ne nous dit pas pourquoi.
Mˆeme s’il n’utilise pas encore ces mots, on sent poindre derri`ere l’analyse de
Turing une question : une d´emonstration d’une proposition Adoit-elle nous dire
que la proposition Aest vraie ou pourquoi elle est vraie ? Et cette question sera
r´ecurrente `a chaque fois qu’un ordinateur sera utilis´e pour r´esoudre un probl`eme
math´ematique : la d´emonstration de Appel et Haken du th´eor`eme des quatre cou-
leurs, ou la d´emonstration de Hales de la conjecture de Kepler, nous disent que ces
propositions sont vraies, mais il est exact qu’elles ne nous disent pas pourquoi.
SMF – Gazette – 135, janvier 2013

ALAN TURING ET LA R´ ESOLUTION NUM´ ERIQUE DES ´ EQUATIONS DIFF´ ERENTIELLES 33
Naturellement, les questions esth´etiques et le sentiment intime de compr´ehension
sont hors du champ des math´ematiques elles-mˆemes, mais il y a aussi des probl`emes
math´ematiques derri`ere ces questions : `a quelle condition pouvons-nous dire qu’une
d´emonstration est explicative ou non ? Et `a supposer que nous parvenions `a une
telle d´efinition, les propositions qui ont une d´emonstration ont-elles toujours
une d´emonstration explicative ? Et pouvons-nous d´emontrer que le th´eor`eme des
quatre couleurs, par exemple, n’a que des d´emonstrations non explicatives ?
Autant de questions auxquelles que nous ne faisons aujourd’hui qu’entrevoir de
maigres ´el´ements de r´eponse.
SMF – Gazette – 135, janvier 2013