7 Notion de fonction

Chapitre
7
Notion de fonction
36
I. Programme de la classe de troisième
Connaissances Capacités Commentaires
1.1. Notion defonction
Image, antécédent,
notations
f(x), x ↦ f(x).
[Thèmes
deconvergence]
–Déterminer l’image d’un nombre par
unefonction déterminée par une courbe,
untableau de données ou une formule.
–Déterminer un antécédent par lecture directe
dans un tableau ou sur une représentation
graphique.
Toute définition générale de la notion de fonction
et la notion d’ensemble de définition sont hors
programme.
La détermination d’un antécédent à partir
del’expression algébrique d’une fonction n’est exigible
que dans le cas des fonctions linéaires ou affines.
II. Contexte du chapitre
L’un des objectifs est de faire émerger progressivement, sur
des exemples, la notion de fonction en tant que processus
faisant correspondre à un nombre, un autre nombre. Les
exemples mettant en jeu des fonctions sont issus de situa-
tions concrètes ou de thèmes interdisciplinaires.
L’utilisation des expressions « est fonction de » ou « varie
en fonction de », amorcée dans les classes précédentes,
est poursuivie et est associée à l’introduction de la
notation f(x).
L’usage du tableur-grapheur contribue aussi à la mise en place
du concept, dans ses aspects numériques comme dans ses
aspects graphiques.
III. Ressources disponibles sur le site compagnon et le manuel numérique Premium
Savoir faire Animation : Déterminer l’image d’un nombre par une fonction.
Animation : Déterminer un antécédent d’un nombre par une fonction.
Exercices PDF à télécharger pour l’exercice 111
Travaux pratiques
avecunordinateur
Pour aider à la correction en videoprojection :
•Figure dynamique de l’activité 1
•Tableur de l’activité 2
•Figure dynamique de l’activité 3
Fichier « boite_noire_07 »
PDF : Fiches-réponses élèves imprimables pour les quatre activités
Du côté du site compagnon PDF : Les courbes remarquables
IV. Intentions pédagogiques
des activités
A. Activités d’introduction
Activité 1 : Vers la notion de fonction
Dans les classes antérieures, les élèves ont travaillé la notion de
fonction au travers de l’usage de la variable dans des exemples
concrets mettant en œuvre du calcul algébrique. L’expression
« en fonction de » est connue depuis la classe de sixième.
Cette activité a pour objectif de réinvestir ces connaissances
afin de les formaliser par l’expression algébrique d’une fonction.
Les notations nouvelles doivent être introduites prudemment
et progressivement.
La fin de l’activité montre qu’une fonction peut être repré-
sentée graphiquement dans un repère. Il s’agit de faire com-
prendre aux élèves que les lectures graphiques qui en décou-
lent facilitent grandement l’interprétation de certains éléments
du problème posé.
Activité 2 : Image d’un nombre par une fonction
La notion d’image d’un nombre par une fonction est nou-
velle bien que connue des élèves de façon intuitive. Dans les
classes antérieures, la substitution d’un nombre inconnu par
une valeur numérique a déjà été pratiquée.
Cette activité réinvestit ce savoir-faire et le formalise. Elle donne
l’occasion d’introduire la notation nouvelle du type
f: x …
.
La détermination d’images passe également par la lecture
d’un tableau de données (question 5) ou la lecture d’un
graphique (Activité 3).
Activité 3 : Antécédent d’un nombre
parunefonction
La lecture graphique facilite l’introduction de la notion d’an-
técédent d’un nombre par une fonction. Elle est intimement
liée à la notion d’image. Le passage réciproque d’un axe à
l’autre du repère en passant par la courbe doit faire preuve
d’une attention particulière.

37
Chapitre 7 • Notion de fonction
7 1. 0 2. 5
8 5
9 1. 3 2. –1, 1 et 2
10 1. 2 est un antécédent de –3 et –1 est un antécédent de 1.
2. g(2) = –3 et g(–1) = 1.
11 Environ 6,5 cm.
Exercices d’entraînement
12
1. 1980 : 800 000 ; 1970 : 850 000 ; 1950 : 850 000 ;
1910 : 825 000.
2. Taux le plus élévé en 1902 ; le plus faible en 1916.
3. En 1915 ; 1920 ; 1935 ; 1945.
4. De 1914 à 1916 et de 1939 à 1941. Ces périodes correspon-
dent aux deux guerres mondiales.
13 1. 6 m ; 3 m ; 4 m.
2. 5 fois.
3. 4 m ; 2,5 m.
4. 1,1 s.
14 1. 70 min.
2. Oui car pour t = 70 minutes, on a d = 0.
3. 20 km.
4. Le cycliste fait une pause de 10 minutes.
5. Entre 50 et 70 minutes de course.
15 1. 6 jours.
2. 10 jours.
3. Entre 4 jours et 20 jours.
4. Après 18 jours.
16 1. A = 7x 2. B = x2 + 5 3. C= x
x4+
17 N = 2x + 5
18 N = xx
2
2+
19 1. c2 2. 2πr 3. 2h
20 À vérifier sur le cahier de l’élève.
21 x2
22 3
5x+
23 x3
2
24 1. f( ) x x= 36 2
π π− .
2. Pour 0 < x < 6.
3. f( ) ,4 20 62 8= π ≈ .
25 L’image de 2 est 4. L’image de –3 est –6.
26 L’image de 3 est 9. L’image de –7 est 49.
27 1. 6 2. –1 3. 10 4. –1 et 15
28 1. 5 2. 3,5 3. 3 4. –5 et 0
29 1. −7
3 2. –2 3. –4 4. 0 et 4
30
L’image de 1 par la fonction f est 2 f(1) = 2 f : 1 ↦ 2
L’image de 3 par la fonction f est –1 f(3) = –1 f : 3 ↦ –1
L’image de 0 par la fonction f est 4 f(0) = 4 f : 0 ↦ 4
L’image de –1 par la fonction f est 5 f(–1) = 5 f : –1 ↦ 5
L’image de 6 par la fonction f est –6 f(6) = –6 f : 6 ↦ –6
L’image de –6 par la fonction f est 6 f(–6) = 6 f : –6 ↦ 6
31 1. f:x x
2 4+ 2. f:x
x
1
2 3.
f
:x x−2
32 1. f(1) = 5 2. f:6
6
3. f(–4) = 5 4.
f:−2–2
L’étude d’un exemple concret permet de débattre de ces
notions et plus particulièrement de l’opportunité qu’a un
nombre de posséder plusieurs antécédents alors qu’un nombre
ne possède qu’une seule image.
Dans l’exemple étudié, à 10 h, on ne peut faire correspondre
qu’une unique valeur pour la hauteur de marée (image unique).
Alors qu’une même hauteur de marée peut correspondre à
plusieurs heures de la journée.
B. Activités TICE
Activité 1 : Programmes de calcul et fonctions
• Considérations didactiques : Le tableur est un outil à pri-
vilégier pour introduire la notion de variable. Les calculs peu-
vent être automatisés ; un changement de valeur dans une cel-
lule entraîne le changement immédiat de l’affichage de toutes
les cellules liées à celle-ci. Dans les programmes de calculs, le
nombre choisi au départ prend le rôle de la variable, le pro-
gramme lui-même correspond à l’expression d’une fonction
qu’il faudra modéliser.
Cette activité donne également l’occasion de faire du calcul
algébrique pour démontrer les résultats conjecturés.
• En pratique : Aucune difficulté technique n’est à attendre si
les élèves ont quelques expériences du tableur. Ce type d’ac-
tivité est un grand classique à résoudre à l’aide du tableur.
Activité 2 : La balle de tennis
• Considérations didactiques : L’utilisation d’un logiciel pour
représenter et modéliser une situation concrète permet d’en
faciliter l’interprétation.
Le logiciel permet d’afficher la courbe représentative de la
fonction et d’y faire glisser un point dont les coordonnées
sont affichées. Il s’agit ainsi d’interpréter les valeurs de ses
coordonnées par rapport au problème posé. Par exemple, lire
les coordonnées (1 ; 2) signifie qu’après 1 seconde, la balle se
trouve à 2 m de hauteur.
• En pratique : Aucune difficulté technique n’est à attendre.
Cette activité est l’occasion de montrer que de nombreux
logiciels permettent de représenter les courbes représenta-
tives de fonctions. C’est aussi l’occasion de débattre de l’en-
semble de définition d’une fonction qui peut dépasser les
contraintes du problème.
Activité 3 : L’enclos de Mathilde
• Considérations didactiques : Cette activité permet de
résoudre un problème d’optimisation en s’aidant d’un logiciel.
Les objectifs didactiques sont identiques à ceux de l’activité 2.
Une difficulté supplémentaire est cependant à envisager :
la modélisation du problème est ici demandée aux élèves.
• En pratique : Aucune difficulté technique n’est à attendre
(voir commentaires de l’activité 2).
Activité 4 : La boîte noire du chapitre 7
La boîte noire du chapitre demande de saisir un nombre et
lui fait correspondre son image par une fonction. L’élève doit
déterminer l’expression de cette fonction.
Il s’agit de la fonction f: x x
2
1
+.
V. Corrigés des exercices
Savoir faire
1 L’image de 3 est 4. L’image de 4 est 3.
2 1. L’image de –2 est 5. L’image de 1 est 0.
2. g(–1) = 7 et g(1) = –3.
3 4 et 4,5.
4 – 4, 6, −48
7, – 8,995.
5 L’image de 1 est –2. L’image de –2 est 0.
6 Réponse C

38
56 a. 3 est un antécédent de 7 par la fonction f.
b. 8,2 est l’image de –5 par la fonction g.
c. 1 est un antécédent de 2,6 par la fonction g.
d. –1 est un antécédent de 9 par la fonction f.
e. 7 est l’image de –3 par la fonction f.
57 4, 1, 0, 1, 4.
58 –2 et 2, –1 et 1, 0.
59 (C1) : f, (C2) : k, (C3) : h, (C4) : g.
60 1. (10 × 3 + 102) × 2 = 260.
2. 20, 44
9, 6 5 10+.
3. 0
61 1. − +
( )
× −
( )
+2 4 2 4
2. 49
3. a. À vérifier sur la copie de l’élève.
b. On obtient un carré parfait.
4. –1
62 1. a. À vérifier sur le cahier de l’élève.
b. À vérifier sur le cahier de l’élève.
c. 3
2. Le programme mène au double du nombre de départ.
( ) x x x+ − −1 1 2
2 2 = .
63 Partie 1 1.
Réduction
en € Prix de la place en € Nombre de spectateurs Recette du spectacle
0 20 500 10 000
1 19 550 550 × 19 =
10 450
2 18 600 600 × 18 =
10 800
416 700 700 × 16 =
11 200
2.
Réduction
en € Prix de la place en € Nombre de
spectateurs
Recette du
spectacle
x20 – x500 + 50x(20 – x)
(500 + 50x)
3. − + [phone]
2
x x  .
Partie 2 1. 11 000 €
2. Réduction : 17 €, prix d’une place : 3 €.
3. R(8) ≈ 10 800.
4. La recette maximale est de 11 300 € pour une place à 15 €.
Parcours autonome
64 C 65 B 66 A 67 B 68 B 69 B et C
70
5
3
+x
71 1
1x+
72 1. 2x2 2. f(6) = 72
73 1. a. f(2) = –1 b. f : 6
16
c. f(–2) = 5 d. f : 5
0
2. 1 et 5 ont pour image 0 ; 3 et 4 ont pour image –5.
74 1. 0, 20 et 18.
2. –1, 4 et 5.
3. Un nombre à peu près égal à 7.
4. 4,5.
75 g(–2) = 14 ; g(0) = 0 ; g 1
2
 = –1 et g(103) = 1 997 000.
76 a. f(5) = 1
23 b. f(2) = 1 2
c. f: 10 
1
98 d. f: 
1−
1 ou
f: −1–1
33 1. a. L’image de –5 par la fonction g est 3.
b. L’image de –2 par la fonction g est égale à 10.
c. –4 a pour image 1 par la fonction g.
2. –10 et 10 ont pour image –6 ; –5 et 3 ont pour image 3 ; –4
et 1 ont pour image 1.
34 1. –100 2. –8, –2 et 6. 3. Oui 4. 100
35 1. –5, –3 et 0.
2. –2, 1 et 1,6.
3. –1,5, –0,5 et 2,4.
4. –5.
36 4
5, 1, 6 5 et 7 5.
37 –8, –9, –8 et 0.
38 g(–2) = –6, g(0) = –4, g(5) = 36, g(10) = 126.
39 Octave a calculé l’image de 3.
40 a. f(5) = 625 b. f(3) = 81
c. f : 107
1028 d. f : 105 1020
41 1. f(0) = 3
5; f(1) = 1 2; f(2) = 3 7; f(3) = 3 8 et f(4) = 1 3.
2. Pour x = 5, le dénominateur s’annule.
42 1. f(–1) = −1
28 , f(0) = −1 30 , f(1)= −1
30 .
2. Pour x = 6, le dénominateur s’annule.
3. Oui, –5.
43 a. Un antécédent de 4 par la fonction f est le nombre –2.
b. Le nombre 4 est un antécédent de 1 par la fonction f.
c. Le nombre 0 est un antécédent de 2 par la fonction f.
44 1. 4 2. 6 3. 5
45 1. 0 2. 2 ou –2 3. 1 4. 2
46 1. 1 2. 3 3. –2 4. 0,5 5. 9
47
2 est un
antécédent de 3
par la fonction f.
3 est l’image de 2
par la fonction f.f(2) = 3 f : 2 ↦ 3
–4 est un
antécédent de 6
par la fonction f.
6 est l’image
de–4 par
lafonction f.
f(6) = –4 f : 6 ↦ –4
5 est un
antécédent de 3
par la fonction f.
3 est l’image de 5
par la fonction f.f(3) = 5 f : 3 ↦ 5
7 est un
antécédent de –3
par la fonction f.
–3 est l’image
de7 par la
fonction f.f(–3) = 7 f : –3 ↦ 7
48 a. 4 b. 2 c. –2,7, –0,5 et 3,6
49 a. 1 ou 4,2 b. 2,5 et 3,7
c. –2, 0, 2 et 4 d. 2
50 a. –2,5, 0, 0,8 ou 3,6. b. –2,6 ou 3,7.
c. –2, –1, 2 ou 3. d. –2
51 a. 3,5 b. 0 c. 7,3 d. 0,4
52 Franck a calculé l’image de 2.
53 1. L’affirmation a.
2. –1 et 1.
3. 3x2 > 0, donc 3x2 + 1 > 1.
54 a. 3 est un antécédent de 0 par la fonction g.
b. 3 est l’image de 2 par la fonction f.
c. 6 est un antécédent de 2 par la fonction h.
d. 0 a pour image –1 par la fonction h.
e. 15 a pour antécédent 5 par la fonction f.
55 a. Faux b. Vrai c. Faux d. Vrai e. Vrai

39
Chapitre 7 • Notion de fonction
91 1. et 2.
v20 40 60 80 100 120 140 160
f(v)2,58 10,32 23,23 41,29 64,52 92,9
126,45 165,16
20 40 60 80 100 120 140 160
180
160
140
120
100
80
60
40
20
0
3. Der Bremsweg eines Fahrzeugs verhält sich nicht propor-
tional zu seiner Geschwindigkeit, da die grafische Darstellung
keine Gerade erzeugt.
92 1. To check the exercise books.
2. To check the exercise books.
3. We assume that the final number of the sequence of calcu-
lations is equal to twice the start number.
4. ( ) 
xx + ×
−
1 4
22 2=
93 1. V = =( )   .xxx
π
π
2
2
6
32
×
2. Non
3. V(3) =
18 56
55π ≈
,
; V(5) =
50 157
08
π ≈ ,
; V(7) =
98 307 88
π ≈
,
.
4. x = 4
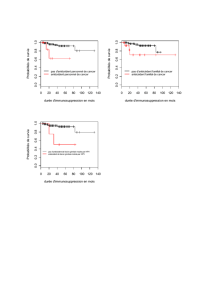
94 Courbe 1 : récipient 2 ; Courbe 2 : récipient 4 ; Courbe 3 :
récipient 1 ; Courbe 4 : récipient 3.
95 1
2
96 9
97 1. f:x x
2 et g:xx
2
1
+
2. Non. f(1) = 1 et g(1) = 1,5.
3. Oui, les valeurs de x égales aux abscisses des points
d’intersection des courbes.
4. x≈ − ,0 8 ou x ≈ 1,3.
98 1. –79, –159, –799. Lorsque les valeurs de x choisies se
rapprochent de 5 tout en lui restant inférieures, les images
correspondantes sont des valeurs négatives de plus en plus
grandes.
2. À vérifier sur le cahier de l’élève.
3. Lorsque les valeurs de x choisies se rapprochent de 5 tout
en lui restant supérieures, les images correspondantes sont
des valeurs positives de plus en plus grandes.
4.
1 2 3 4 5 6 7 8 9
100
80
60
40
20
0
–20
–40
–60
77 1. 1010 2. 10–8 3. 1010
78 1. 0 2. 10 3. –1 4. –1,9 5. –6
79 a. –1 b. 0 c. 2 d. 1,1
80 a. –2 ;
b. –1 ; 3,8 et 5 ;
c. –0,5 ; 1,6 et 6,2 ;
d. 4,5.
81 1. a. et c. 2. –2
Exercices d’approfondissement
82 1. 4,5 m puis 5,8 m.
2. 0,8 s.
3. 5,8 m après 1 s.
4. 2 s.
83 1. À vérifier sur le cahier de l’élève.
2. Il y a une forte augmentation démographique à partir de
1900.
3. Entre 1200 et 1400.
84 1. Programme 1 : 14 et Programme 2 : 64.
2. Programme 1 : g et Programme 2 : f.
3. Choisir un nombre ; lui ajouter 3 ; élever au carré.
85 1. 8, 27
8, 10–3, 1018.
2. 2 1012
×, 2 10 20
×−, 3 2 1021
,×, 2 43 10 14
,×−.
86 1. –8,4, –1,6, 7,2, 18
2.
x3 3,1 3,2 3,3 3,4 3,5 3,6
f(x)–1,6 –0,81 0 0,83 1,68 2,55 3,44
3. 3,2.
87 1.
x–1,2 –1 –0,8 –0,6 –0,4 –0,2 0 0,2 0,4
f(x)
5,04 4 3,04 2,16 1,36 0,64 0 –0,56 –1,04
x0,6 0,8 1 1,2 1,4 1,6 1,8 2
f(x)–1,44 –1,76 –2 –2,16 –2,24 –2,24 –2,16 –2
2. À vérifier sur le cahier de l’élève.
88 1. 0
2. g(4) = –2.
3. Non car g(10) ≠ –1.
4. Pour x = 5, le dénominateur s’annule.
89 1. v
t
= 500
2. v(5) = 100, v(6) = 250
3, v(7) = 500 7.
3. Environ 91 km/h.
4. Environ 79 km/h.
5. a. t = 6,25.
b. 6,25.
c. Odette parcourt une distance de 500 km durant 6 h 15 min
à la vitesse moyenne de 80 km/h.
90 1. EF =×x 400.
2. A( x)=AB ×AD= x−2−2
( )
400
x−2−2
⎛
⎝
⎜⎞
⎠
⎟
=
x−4
( )
400
x−4
⎛
⎝
⎜⎞
⎠
⎟.
3.
x5 7,5 10 12,5 15 17,5 20 22,5
A(x)76 172,7 216 238 249,3 254,6 256 254,9
x25 27,5 30
A(x)252 247,8 242,7
4. À vérifier sur le cahier de l’élève
5. x = 20.

40
3.
1234567891011
30
25
20
15
10
5
0
2
1. g(0) < f(0) < h(0).
2. f(–1) > h(–1) > g(–1).
3. g(2) > h(2).
4. a. x = 2 et x = –5.
b. Non car g(2) = 1 et h(–5) = 1.
5. Pour x = –6, le dénominateur s’annule.
6. 3x2 > 0
5. Autour des points d’abscisse 5, la courbe s’étire vers le haut
et le bas du repère.
6. Non. Pour x = 5, le dénominateur s’annule.
Devoir à la maison
1
1.
xx2x2
2
x2
2
5+3xf( ) 25 3
2
xxx   = + −
00 0 5 0 5
11 0,5 5,5 3 2,5
2 4 2 7 6 1
39 4,5 9,5 9 0,5
416 8 13 12 1
525 12,5 17,5 15 2,5
636 18 23 18 5
749 24,5 29,5 21 8,5
864 32 37 24 13
981 40,5 45,5 27 18,5
10 100 50 55 30 25
2. f(2) = 1.