Les unités

les unités td 2006 page 1 / 2
Les unités
Les unités sont nécessaires pour comparer les valeurs de différentes grandeurs physiques. Elles sont aussi
utiles pour vérifier la pertinence d'expressions littérales.
Les unités du système international (S.I.)
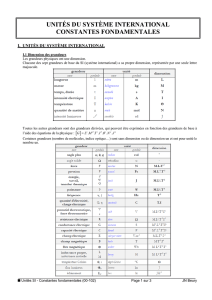
Le système international d'unités est construit autour de 7 unités
de base qui correspondent à 7 grandeurs fondamentales
différentes [Doc. 1]. Il comporte aussi des unités supplémentaires
(le newton pour la force, le volt pour la tension…) appelées unités
dérivées. Ces unités dérivées peuvent être exprimées en fonction
des unités de base.
On ne peut additionner ou soustraire que des valeurs numériques
exprimées dans la même unité.
L'unité du produit de deux grandeurs est le produit des unités de
chacune des grandeurs.
Plus d'infos sur le site du Bureau International des Poids et Mesures : http://www.bipm.fr/fr/si/
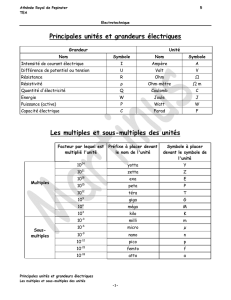
Multiples et sous multiples
La valeur de l'unité n'est pas toujours adaptée à l'ordre de grandeur
du résultat numérique d'une mesure ou d'un calcul. On peut alors
utiliser la notation scientifique pour exprimer ce résultat ou utiliser
un multiple ou sous-multiple de l'unité [Doc. 2].
Les multiples et sous multiples d'une unité sont nommés à partir du
nom de l'unité auquel on ajoute un préfixe qui symbolise le
coefficient multiplicateur.
Remarque : le multiple kilo (k) ne doit pas être confondu avec le kilo
informatique (K) dont le coefficient multiplicateur est 1024.
Analyse dimensionnelle
L'analyse dimensionnelle permet de vérifier l'homogénéité d'une formule littérale. Pour cela on relie aux unités S.I.
les diverses grandeurs physiques qui interviennent dans cette formule.
Exemple 1 : onde le long d'une corde tendue
La vitesse d'une onde transversale qui se propage le long d'une corde dépend de la force de tension F de
la corde (en newton) et de la masse linéique
µ
de cette corde (en kilogramme par mètre). Elle est donnée
par
µ
F. En raisonnant sur les unités, montrons que cette expression est homogène a une vitesse.
Le poids est une force. Dans le système international il s'exprime en newton. Considérons un corps dont la masse en
kilogramme est masse m. Le poids de ce corps est P = m·g. L'intensité g de la pesanteur s'exprime donc en N·kg-1.
La conservation de l'énergie étudiée en 1èreS montre que g s'exprime aussi, avec la même valeur numérique, en m·s-2.
Cela conduit à l'égalité entre les unités : 1 N·kg-1 = 1 m·s-2. Le newton peut donc être exprimé en fonction des unités de
base du système S.I. : 1 N = 1 kg·m·s-2. Le newton est une unité dérivée du système international.
Dans le système international,
µ
F s'exprime donc en 1
2
mkg
smkg
−
−
⋅
⋅⋅ =
1/2
1
2
mkg
smkg 
⋅
⋅⋅
−
−=
(
)
1/2
22 sm −
⋅=1 sm − ⋅. Cette
expression est bien homogène a une vitesse.
Exemple 2 : vague à la surface de l'eau
En eau peu profonde, la vitesse d'une vague dépend de l’intensité g de la pesanteur et de la profondeur h
de l’eau. Elle est donnée par hg ⋅. Montrons que cette expression est homogène a une vitesse.
Dans le système international hg ⋅ s'exprime en msm 2- ⋅⋅ = 2-2 sm ⋅ = m·s–1. Cette expression est homogène a
une vitesse.
Grandeur Unité S.I.
longueur (L) mètre (m)
masse (M) kilogramme (kg)
temps (T) seconde (s)
intensité électrique ()ampère (A)
température kelvin (K)
intensité lumineuse candela (cd)
quantité de matière mole (mol)
Doc. 1 Les sept unités de base du système
international et les sept grandeurs fondamentales.
nom symbole coefficient
giga G 109
méga M 106
multiples
kilo k 103
milli m 10-3
micro µ10-6
sous-
multiples
nano n 10-9
Doc. 2 Quelques multiples et sous multiples.

les unités td 2006 page 2 / 2
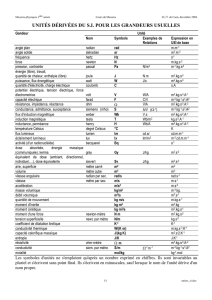
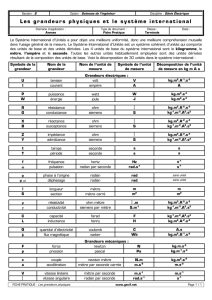
Des unités dérivées du système international (S.I.)
À partir des 7 unités de base qui correspondent à 7 grandeurs fondamentales différentes on peut définir de nombreuses
autres unités qui correspondent à d'autres grandeurs.
Grandeurs Unités S.I.
nom symbole expression nom symbole expression
longueur L (ou d…) mètre m
masse m ou Mkilogramme kg
temps t ou T ou τseconde s
intensité
électrique i ou ampère A
température T ou θkelvin K
intensité
lumineuse L ou ILcandela cd
quantité de
matière n
7 grandeurs
fondamentales
mole mol
surface S S = a x b pour un
rectangle mètre carré m2
volume V S = a3 pour un
cube mètre cube m3
vitesse v v = d / t mètre par
seconde m·s-1
accélération a a = v / t mètre par
seconde au carré m·s-2
force F F = m x a newton N kg·m·s-2
pression P P = F / S pascal P kg·m-1·s-2
charge
électrique q ou Q Q = i x  coulomb C A·s
tension
électrique u ou U u = F x d / Q volt V kg·m2·A-1·s-3
puissance P P = F x v
ou P = u x i watt W kg·m2·s-3
= V·A
énergie E ou W E = P x t joule J kg·m2·s-2
= V·A·s
fréquence f ou N f = 1 / T hertz Hz s-1
résistance
électrique R R = u / i ohm Ωkg·m2·A-2·s-3
= V·A-1
conductance
électrique G G = 1 / R = i / u siemens S kg-1·m-2·A2·s3
= Ω-1 = V-1·A
conductivité σσ = G x L / S kg-1·m-3·A2·s3
= S·m-1
conductivité
molaire
ionique λλ = σ / (n / V) kg-1·A2·s3·mol-1
= S·m2·mol-1
capacité d'un
condensateur C C = Q / u farad F kg-1·m-2·A2·s4
= C·V-1 = s·Ω-1
inductance
d'une bobine L L = u/(di/dt) henry H kg·m2·A-2·s-2
= V·s·A-1 = s·Ω
Attention
- Il ne faut pas confondre le symbole d'une grandeur et le symbole d'une unité, par exemple la lettre C est le symbole
de la grandeur "capacité", c'est aussi le symbole de l'unité "coulomb".
- Il y a des confusions possibles entre diverses grandeurs, par exemple la puissance et la pression sont généralement
symbolisée par la lettre "P", la vitesse et le volume par la lettre "V ou v". Les unités permettent souvent d'éviter des
confusions…