Recherche des isométries du plan conservant un polygone régulier

𝑛
𝑂
𝜃2𝑘𝜋/𝑛 𝑘 ∧𝑛= 1
𝑃
𝑃
𝐼𝑠(𝑃)𝐼𝑠(𝐸)
𝐼𝑠(𝑃)⊂𝐼𝑠(𝑆)
𝑓∈𝐼𝑠(𝑃)
𝐼𝑠+(𝑃)
𝐼𝑠+(𝑃)𝐼𝑠(𝑃)
𝐼𝑠+(𝑃) = {𝐼𝑑, 𝑟, . . . , 𝑟𝑛−1}
𝐼𝑠−(𝑃)
𝐼𝑠−(𝑃) = {𝑠, 𝑠𝑟, 𝑠𝑟2, . . . , 𝑠𝑟𝑛−1}𝐼𝑠−(𝑃)
𝑛 𝑛
𝑂 𝜃
𝑋⊂𝐸 𝐼𝑠(𝑋)𝐼𝑠+(𝑋)𝐼𝑠−(𝑋)
𝐼𝑠(𝑋)≤𝐼𝑠(𝐸)𝐼𝑠+(𝑋)⊴𝐼𝑠(𝑋)
𝐼𝑠−(𝑋)𝑠𝐼𝑠+(𝑋)
𝐼𝑠(𝑋)
𝑓∈𝐼𝑠(𝑃)
𝐼𝑠(𝑃) = 𝐼𝑠(𝑆)
𝐼𝑠+(𝑃)
𝐼𝑠+(𝑃) =< 𝑟 >
𝐼𝑠+(𝑃)≃ℤ/𝑛ℤ
𝐼𝑠−(𝑃)
𝐼𝑠−(𝑃) = {𝑠, 𝑠𝑟, . . . , 𝑠𝑟𝑛−1}
𝑛 𝑛
𝐼𝑠(𝑃)∣𝐼𝑠(𝑃)∣𝐼𝑠(𝑃)≃𝔻𝑛
𝑄∣𝑄∣=𝑛 𝐼𝑠(𝑄)=2𝑛
𝔻𝑛=ℤ/𝑛ℤ⋊ℤ/2ℤ

𝐼𝑠(𝑃) =< 𝑟, 𝑠 > 𝑟𝑛=𝐼𝑑 𝑠2=𝐼𝑑 (𝑟∘𝑠)2=𝐼𝑑
𝐼𝑠(𝑃)𝑅={𝐼𝑑, 𝑟, 𝑟2, . . . , 𝑟𝑛−1}ℤ/𝑛ℤ𝑆={𝐼𝑑, 𝑠}
ℤ/2ℤ𝐼𝑠(𝑃)𝑓∘𝑔 𝑓 ∈𝑅 𝑔 ∈𝑆
(𝑘, ℓ)𝑘∈ℤ/𝑛ℤℓ∈ℤ/2ℤ
𝑓=𝑟𝑚𝑔=𝑠𝜀𝑚∈ {0, . . . , 𝑛 −1}𝜀∈ {0,1}(𝑘, ℓ) = (𝑚, 𝜀)
(𝑓∘𝑔)∘(𝑓′∘𝑔′)
𝑠∘𝑟=𝑟−1∘𝑠(𝑖, 𝑗)∈ {0, . . . , 𝑛 −1}2(𝜀, 𝛿)∈ {0,1}2
(𝑟𝑖∘𝑠𝜀)∘(𝑟𝑗∘𝑠𝛿)=(𝑟𝑖∘𝑠𝜀∘𝑟𝑗∘𝑠−𝜀)∘(𝑠𝜀𝑠𝛿)
𝜀= 0 𝑟𝑖∘𝑠𝜀∘𝑟𝑗∘𝑠−𝜀=𝑟𝑖+𝑗𝜀= 1 𝑟𝑖∘𝑠𝜀∘𝑟𝑗∘𝑠−𝜀=𝑟𝑖−𝑗
ℤ/𝑛ℤ×ℤ/2ℤ𝐼𝑠(𝑃)
(𝑖, 𝜀)∗(𝑗, 𝛿)=(𝑖+ (−1)𝜀𝑗, 𝜀 +𝛿)
(𝑥, 𝑦)∗(𝑥′, 𝑦′) = (𝑥+𝑥′, 𝑦 +𝑦′)
ℤ/2ℤ ℤ/𝑛ℤ
𝐼𝑠(𝑃)𝑛
𝐼𝑠(𝑃)𝐺 𝐺 𝐺
𝐺
𝑍(𝐺) = {𝑓∈𝐺 / ∀𝑔∈𝐺, 𝑓 ∘𝑔=𝑔∘𝑓}
𝐼𝑠(𝑃) = {𝐼𝑑, 𝑟, . . . , 𝑟𝑛−1, 𝑠 ∘𝑟, 𝑠 ∘𝑟2,...𝑠∘𝑟𝑛−1}𝑟
𝑂2𝑘𝜋/𝑛 𝑘 ∧𝑛= 1 𝑠 𝑂
𝐼𝑑 ∈𝑍(𝐼𝑠(𝑃)) 𝐼𝑑 𝑍(𝐼𝑠(𝑃))
𝑟 𝑟′
𝑟 𝑟′
𝑠 𝑠′
𝑠=𝑠′𝑠∘𝑠′
𝑠 𝑠′𝑂 𝑠 ∘𝑠′
𝑠=𝑠′𝑠∘𝑠′
𝑠∘𝑟 𝑟 =𝐼𝑑 𝑟 𝜋
𝑟 𝑠
𝑓∈𝑍(𝐼𝑠(𝑃)) 𝑛−1𝑛−1
𝐼𝑠(𝑃)
𝑓∈𝑍(𝐼𝑠(𝑃)) 𝑓∕=𝐼𝑑 𝑂 𝑛 −2
𝜋
𝜋 𝐼𝑠(𝑃)𝑛 𝑛
𝑂
𝑍(𝐼𝑠(𝑃)) = {𝐼𝑑𝐸}𝑛 , 𝑍(𝐼𝑠(𝑃)) = {𝐼𝑑𝐸, 𝑟𝑛/2}𝑛
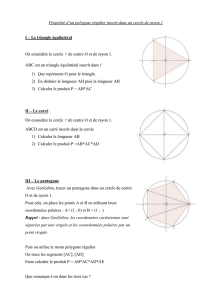
𝑂 𝐴
𝐵=𝑠𝑂(𝐴)𝐶=𝑚𝑖𝑙[𝑂𝐵]𝐼=𝑚𝑖𝑙[𝑂𝐶] [𝐴𝐵]
𝑂 𝐷 𝐽 =𝑚𝑖𝑙[𝑂𝐷]𝒞′
𝐼 𝐽 [𝐴𝐵]𝑀 𝑁
[𝐴𝐵]𝑀 𝑁
𝐼𝐽 =√5/4𝑁∈[𝑂𝐴]𝑂𝑁 = (√5−1)/4 = 𝑅𝑒(𝑒2𝑖𝜋/5)
𝐵=𝑠𝑂(𝐴)𝐴𝐵 𝑂
𝐶 𝐼 =𝑚𝑖𝑙[𝑂𝐶]𝒞′𝐼 𝑂 (𝐵𝐼)
𝒞′𝐸 𝐹 𝐵 𝐸 𝐹
𝐼𝐵 =√5/2𝐵 𝐹 𝐹 ∕∈ [𝐼𝐵]𝐼𝐵 + 1/2
∣𝜔−1∣𝜔 𝑅𝑒(𝜔)=(√5−1)/4 = 𝑅𝑒(𝑒2𝑖𝜋/5)