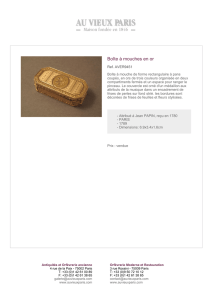
Frises et Algèbres Non-Associatives - IMJ-PRG

Université Pierre et Marie Curie
MÉMOIRE
présenté pour l’obtention de
l’HABILITATION À DIRIGER DES RECHERCHES
(Spécialité : Mathématiques)
sur les
« Frises et Algèbres Non-Associatives »
par
Sophie Morier-Genoud
Soutenu le 3 Décembre 2014
RAPPORTEURS
M. Frédéric Chapoton (Université Claude Bernard Lyon)
M. Alberto Elduque (Universidad de Zaragoza)
M. Sergey Fomin (University of Michigan)
JURY
M. Frédéric Chapoton (Université Claude Bernard Lyon)
M. Alberto Elduque (Universidad de Zaragoza)
M. David Hernandez (Université Paris Diderot)
M. Ilia Itenberg (Université Pierre et Marie Curie)
M. Bernard Leclerc (Université de Caen Basse Normandie)

i
Résumé
Ce mémoire consiste en deux parties indépendantes. La première partie porte sur des
généralisations des frises de Coxeter. On étudie en particulier une variante appelée 2-frises,
en interaction avec la théorie des algèbres amassées. On établit une trialité entre les frises, les
équations linéaires en différence et les espaces de modules de polygones. Cette trialité permet
notamment d’utiliser la géométrie projective pour étudier les frises et les équations, mais
aussi d’utiliser les algèbres amassées pour étudier les espaces de polygones. La transformée
de Gale est définie dans le cadre de cette trialité, induisant des isomorphismes non triviaux
entre différents espaces de frises ou différents espaces d’équations.
Dans la deuxième partie on étudie des algèbres non-associatives. On présente tout d’abord
une série d’algèbres généralisant l’algèbre des octonions. Cette série est construite en utilisant
une combinatoire binaire qui se révèle efficace dans la résolution du problème de Hurwitz sur
les identités en sommes de carrés. On propose alors des constructions explicites de nouvelles
identités. On termine en présentant une classe particulière d’algèbres de Jordan pour laquelle
on développe la théorie des représentations et des exemples construits à partir de surfaces de
Riemann marquées.
Abstract
This dissertation consists in two independent parts. The first part deals with generaliza-
tions of Coxeter friezes. We study the variant of so-called 2-friezes, using the theory of cluster
algebras. We establish a “triality” between the spaces of friezes, the linear difference equations
and the moduli spaces of polygons. This triality makes possible the use of projective geome-
try to study friezes and equations, as well as the use of cluster algebras to study the spaces
of polygons. The combinatorial Gale transform is defined within this triality, and provides
isomorphisms between different spaces of friezes and of difference equations.
In the second part, we study nonassociative algebras. We define a series of algebras ge-
neralizing the algebra of octonions. This series is constructed from binary combinatorics and
it is applied to the classical Hurwitz problem of sums of squares identities. In particular, we
give explicit constructions of new identities. In the end of the dissertation, we present a spe-
cial class of Jordan superalgebras, for which we develop representation theory and construct
examples based on punctured Riemann surfaces.

ii

iii
Contents of the dissertation
This dissertation consists in two independent parts : Frieze Patterns and Non-Associative
Algebras. The problems studied, and the methods used in each of these parts contain algebra,
combinatorics and representation theory.
Presented papers
The results presented in the dissertation are published in the following research papers. Other
references are cited by letters and listed at the end of the dissertation.
Part I : Frieze patterns
[1] S. Morier-Genoud, V. Ovsienko, S. Tabachnikov. 2-Frieze patterns and the cluster
structure of the space of polygons. Ann. Inst. Fourier 62 (2012), 937–987.
[2] S. Morier-Genoud. Arithmetics of 2-friezes. J. Algebraic Combin. 36 (2012), 515–
539.
[3] S. Morier-Genoud, V. Ovsienko, R. E. Schwartz, S. Tabachnikov, Linear difference
equations, frieze patterns and combinatorial Gale transform, Forum Math. Sigma 2
(2014), e22.
[4] S. Morier-Genoud, V. Ovsienko, S. Tabachnikov. SL2(Z)-tilings of the torus, Coxeter-
Conway friezes and Farey triangulations, 2014, Ens. Math., to appear.
Part II.1, II.2 : Non-associative algebras (generalized octonions, Hurwitz square identities)
[5] S. Morier-Genoud, V. Ovsienko, Well, Papa, can you multiply triplets ?, Math.
Intell. 31 (2009), 1–2.
[6] S. Morier-Genoud, V. Ovsienko, Simple graded commutative algebras, J. Algebra.
323 (2010), 1649–1664.
[7] S. Morier-Genoud, V. Ovsienko, A series of algebras generalizing the octonions and
Hurwitz-Radon identity, Comm. Math. Phys. 306 (2011), 83–118.
[8] A. Lenzhen, S. Morier-Genoud, V. Ovsienko, New solutions to the Hurwitz problem
on square identities, J. Pure Appl. Algebra 215 (2011), 2903–2911.
[9] S. Morier-Genoud, V. Ovsienko, Orthogonal designs and a cubic binary function,
IEEE Trans. Information Theory, 59 :3 (2013) 1583–1589.
[10] S. Morier-Genoud, V. Ovsienko, Extremal set theory, cubic forms on Fn
2and Hur-
witz square identities (avec V. Ovsienko), arXiv :1304.0949, submitted.
[11] M. Kreusch, S. Morier-Genoud, Classification of the algebras Op,q, 2014, Comm
Alg, to appear.