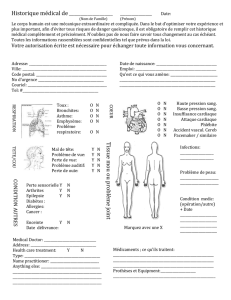
I- Deux exemples:

NOMBRE DE DIAGONALES D'UN POLYGONE
I- Deux exemples:
Pentagone: Le point A est joint à C et D
Le point B est joint à D et E
Le point C est joint à E et A
Le point D est joint à A et B
Le point E est joint à B et C
On a donc tracé 5 x 2 = 10 segments
Mais en fait chacun est compté 2 fois.
Par exemple: [AB] et [BA]
Il faut donc diviser le résultat ci-dessus par 2
Un pentagone a donc 10 : 2 = 5 diagonales
Hexagone: Le point A est joint à C, D et E
Le point B est joint à D, E et F
Le point C est joint à E, F et A
Le point D est joint à F, A et B
Le point E est joint à A, B et C
Le point F est joint à B, C et D
On a donc tracé 6 x 3 = 18 segments
Mais en fait chacun est compté 2 fois.
Par exemple: [AB] et [BA]
Il faut donc diviser le résultat ci-dessus par 2
Un hexagone a donc 18 : 2 = 9 diagonales
II- Méthode générale:
En se basant sur les deux exemples ci-dessus, on remarque que
- chaque sommet est joint à tous les autres sommets moins trois (lui-même et les deux sommets
qui lui sont consécutifs): le nombre de segments ainsi obtenu est donc le produit du nombre de
sommets par le nombre de sommets diminué de 3.
- chaque segment ainsi tracé est compté deux fois; il faut donc diviser le résultat ci-dessus par 2.
Donc:
Le nombre de diagonales d'un polygone est égal à:
[nombre de sommets x (nombre de sommets - 3)] : 2
Exemples:
Pour un octogone: (8 x 5) : 2 = 40 : 2 = 20 diagonales
Pour un décagone: (10 x 7) : 2 = 70 : 2 = 35 diagonales
Pour un dodécagone: (12 x 9) : 2 = 108 : 2 = 54 diagonales
1

POLYGONES REGULIERS
I- Définition:
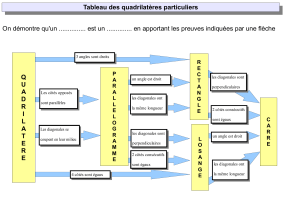
On dit qu'un polygone est régulier si:
- tous ses côtés ont la même longueur
- tous ses angles sont égaux
II- Exemples:
Pentagone régulier Hexagone régulier Octogone régulier
2