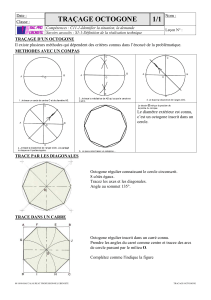
Modèle mathématique.

Chapitre 16 :
Polygones réguliers
Un polygone est une figure fermée constituée de segments.
Un polygone est régulier quand tous ses côtés ont la même longueur et tous ses
angles ont la même mesure. Le polygone régulier peut s’inscrire dans un cercle
dont le centre est l’intersection des axes de symétrie.
1) Construction d’un carré de centre O :
Définition : un carré est un quadrilatère qui a ses quatre côtés de la même
longueur et ses quatre angles droits.
Propriété : un quadrilatère qui a ses diagonales perpendiculaires, de la même
longueur et qui se coupent en leur milieu est un carré.
Pour construire le carré de centre O de sommet A tel que OA = 3 cm, on
commence par tracer ses diagonales :
O A
On trace le segment [OA] que l’on prolonge de 3 cm de l’autre côté du point O.
Puis on construit le segment perpendiculaire à [OA] de longueur 3 cm que l’on
prolonge aussi de 3 cm de l’autre côté du point O.
Ces deux segments perpendiculaires, de la même longueur et qui se coupent en
leur milieu sont les deux diagonales du carré. Leurs extrémités sont les
quatre sommets du carré que l’on relie.
Remarque : On peut construire le cercle de centre O passant par A : ce cercle
contient aussi tous les autres sommets du carré.

2) Construction d’un octogone de centre O :
Un octogone est un polygone de 8 côtés.
Pour construire l’octogone de centre O et de sommet A tel que OA = 3 cm, on
procède comme pour le carré mais on rajoute deux diagonales
perpendiculaires :
45°45
O A
On trace [OA] que l’on prolonge de 3 cm et on trace un segment
perpendiculaire à [OA] que l’on prolonge aussi de 3 cm.
Puis on trace un autre segment de 3 cm qui fait un angle de 45° vers le haut
avec [OA]. On prolonge ce segment.
De même on trace un segment de 3 cm qui fait un angle de 45° vers le bas
avec [OA]. On prolonge aussi ce segment.
On obtient les quatre diagonales de l’octogone avec ses 8 sommets que l’on
relie.
Remarques :
● attention à bien construire les quatre diagonales de la même longueur !
● On peut construire le cercle de centre O passant par A, qui contient aussi
tous les autres sommets de l’octogone.

3) Hexagone et triangle équilatéral de centre
O :
Un hexagone est un polygone de 6 côtés, un triangle est un polygone de 3
côtés.
● Pour construire l’hexagone de centre O et de sommet A, on commence par
tracer le cercle de centre O et de rayon OA :
A
Avec le compas et sans changer l’écartement, on fait des petits arcs de cercle
à partir du point A (comme pour faire une rosace).
On obtient les 6 sommets de l’hexagone que l’on relie.
● Pour construire le triangle équilatéral de centre O et de sommet A, on
procède comme pour l’hexagone en reliant un sommet sur deux.( 3 sommets)
A
x O
x O

Annexe : extrait du programme officiel :
Polygones réguliers.
Construire un triangle équilatéral, un carré, un hexagone régulier, un octogone connaissant
son centre et un sommet.