[24-25]Enoncé-Des-Exos-Colle-Analyse-4-MP-EPO(VersionEtudiant)

Année Académique : 2024-2025
EPO/CPEI/MP-2A Module : Analyse IV
Banque de Sujets de Colle d’Analyse IV pour les Etudiants
(Colles-MP-2A)
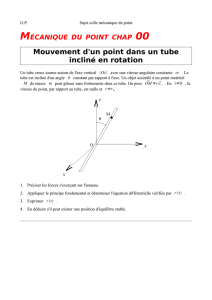
On considère la fonction f:R2−→ Rdéfinie par : f(x, y) = (x3−y3
x2+y2si (x, y)̸= (0,0)
0si (x, y) = (0,0).
1. Etudier la continuité de fen (0,0).
2. Montrer que fadmet des dérivée partielles première en (0,0) et les calculer.
3. fest-elle différentiable en (0,0) ?
Exercice 1 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
Soit f(x, y) = 
y2sin x
ysi y̸= 0
0si y= 0
.
1. Déterminer le plus grand sous-ensemble de R2sur lequel fest de classe C1.
2. Montrer que ∂2f
∂x∂y (0,0) et ∂2f ∂y∂x (0,0) existent et sont différents.
3. Conclure.
Exercice 2 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
1. Calculer la limite suivante : lim
(x,y,z)→(1,0,1)
(x2−z2) ln(1 + y)
√xy −√yz .
2. Soient (Ω,∥∥)un espace vectoriel normé (e.v.n.), θ∈Ω,α∈]1; 2[ et φune application de Ω
vers Ω. On définie la fonction Ψsur l’e.v.n Ωpar,
Ψ : Ω −→ Ω, x 7−→ Ψ(x) = φ1
αθ+1−1 αx.
Montrer que : si φest √3-lipschitzienne alors Ψadmet un unique point fixe.
Exercice 3 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
1

1. On considère la fonction f: (x, y)7−→ x3+ 3x2y−15x−12y
(a) fest-elle coercive ?
(b) Etudier les extremums de f.
2. Résoudre les équations aux dérivées partielles suivantes : (E):2∂f (x, y)
∂x −∂f(x, y) ∂y = 0.
Indication : on pourra poser : u=x+yet v=x+ 2y.
Exercice 4 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
Soit U=(x, y)∈R2|xy ̸= 1, et fune fonction définie sur Upar :
∀(x, y)∈U, f(x, y) := arctan(x) + arctan(y)−arctan x+y
1−xy .
1. Montrer que Uest un ouvert de R2, puis que fest de classe C1sur U.
2. Calculer la Gradient de fsur U.
3. une expression simplifiée de fsur U
Exercice 5 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
1. Calculer la limite suivante : lim
(x,y)→(0,0) lim
n→+∞
n
X
m=0
Em1−cos(xy)
x2y2
n2
2. Soit φ:R2−→ R2,(x, y)7−→ (ex−ey, x +y)une application.
Montrer φest un C1-difféomorphisme de R2sur lui-même.
Exercice 6 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
Dans R, on définit la fonction fpar :
f(x, y) = 3 + sin(x) + cos(y)
4sin(y)
.
1. Montrer que fest définie, continue et différentiable sur R2.
2. Calculer le développement limité de fau voisinage de (0,0) à l’ordre 3.
3. En déduire ∂f
∂x (0,0) et ∂f ∂y (0,0).
4. Calculer le gradient de fsur R2, puis vérifier le résultat de la question 3).
Exercice 7 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
2

1. Calculer la limite suivante : lim
(x,y,z)→(0,0,0)
2x3+yz2̸=0
xyz +z3
2x3+yz2.
2. Calculer la plus petite distance du point (1,0,−2) au plan (P) : x+ 2y+z−4=0
Exercice 8 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
Pour (x, y)∈R2, on pose f(x, y) = 
xy(x2−y2)
x2+y2si (x, y)̸= (0,0)
0si (x, y) = (0,0)
.
Montrer que fest de classe C1sur R2.
Exercice 9 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
1. Calculer la limite suivante : lim
(x,y,z)→(0,0,0)
(x,y,z)̸=(0,0,0)
xy +yz
x2+ 2y2+ 3z2.
2. Une boîte rectangulaire sans couvercle doit être fabriquée avec une feuille d’un metal précieux
d’une aire de 12 m2.
Déterminer ses dimensions pour son volume maximal.
Exercice 10 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
Soit fla fonction de R2dans Rdéfinie par :
f(x, y) = xpyq
x2−xy +y2si (x, y) = (0,0)
f(0,0) = 0.
Où pet qsont des entiers non nuls.
1. Démontrer que, pour tout (x, y)∈R2réels, |xy| ≤ x2−xy +y2
2. Pour quelles valeurs de pet qcette fonction est-elle continue ?
3. Monter que fest différentiable au point (1,1), puis déterminer sa différentielle en ce point.
4. Etudier la différentiabilité de fsur son domaine de définition lorsque p+q= 2.
Exercice 11 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
3

1. Soient nest entier supérieur à 5et T:M
n(R)−→ R, A 7−→ Trace(A).
Etudier la différentiabilité de T, puis déterminer sa différentielle en tout A∈M(R).
2. Soit (E, ∥ ∥)un espace vectoriel normé, B={x∈E| ∥x∥<1}et f:E−→ R, x 7−→ x
1 + ∥x∥.
Montrer que fest un homéomorphisme.
Exercice 12 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
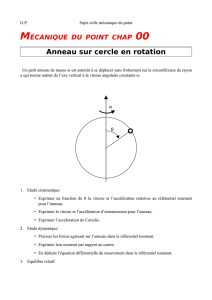
Soit (P)le problème défini par :
(P) min
(x,y)∈R2f(x, y) = x4
4−x2y+y2 2+ 2y+ 1.
1. (P)admet - il des solutions ? Dites si il existe un maximum pour fsur R2?
2. Calculez le gradient de fet déterminer ses points stationnaires.
3. A l’aide de la dérivée seconde de fdites si les points stationnaires trouvés en 1.(b) sont des
minima/maxima/points d’inflexion locaux ou globaux ? (on calculera la valeur de fen ces
points)
Exercice 13 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
1. Rappeler les 4 grands théorèmes du calcul différentiel.
2. Soit n∈N∗, et l’application f:Mn(R)−→ Mn(R), A 7−→ A−1.
3. Déterminer le domaine de définition D
fde f.
4. Montrer que fest différentiable en tout point de D
fet déterminer sa différentielle.
Exercice 14 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
1. Etudier l’existence et la valeur éventuelle de la limite suivante : px2+y2
|x|p|y|+|y|p|x|en (0,0).
2. Une boîte rectangulaire sans couvercle doit être fabriquée avec une feuille d’un metal précieux
d’une aire de 12 m2.
Déterminer ses dimensions pour que son volume soit maximal.
Exercice 15 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
4

Soit Φla fonction définie par : Φ : R3−→ R3,(x, y, z)7−→ 2024xy, (xyz)2024,Argsh(z)
1. Déterminer le domaine Dfde différentiabilité de f.
2. (0,0,0) est - il dans Df? Si oui déterminer la différentielle de Φen (0,0,0).
3. On pose X0= (1,1,0).
(a) Calculer : div(Φ)(X0)et rot(Φ)(X0).
(b) Φest - elle inversible au voisinage de X0?
Exercice 16 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
Soit la fonction fde R2dans Rdefinie par :
f(0,0) = 0,et f(x, y) = xy −3x3+ 7y3
x2+y2,ailleurs.
1. En revenant aux définitions calculer ∂f
∂x et ∂f ∂y en (0,0).
2. En utilisant les formules classiques, calculer ∂f
∂x et ∂f ∂y ailleurs.
3. Ecrire la différentielle de fau point (0,0)
Exercice 17 EPO/CPEI/MP-2A (2024-2025) : Colle d’Analyse IV
✁.............................................. ........ ⋗
5