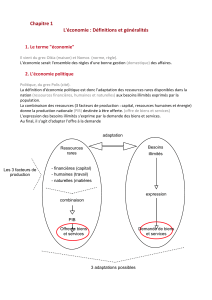
Anisotropie élastique

____________________________________________ page 1 _____________________________________________
Élasticité anisotrope
Marc François version du 25 octobre 2004
Sur cette transformation (non élastique !), la nature l'effet de l'anisotropie sont bien visibles: à
gauche la roche native est visiblement feuilletée ; à droite, après une traction ou compression
uniaxiale, la déformée prend une allure surprenante selon l'orientation des feuillets. (J.P. Boehler).
1) Bases de tenseurs
1.1 Vecteurs (rappels)
Soit ei une base orthonormée. On a ei.ej=δij
On considère la transformation orthogonale R. Ce peut être par exemple une rotation ou une
symétrie. Elle est complètement définie par la matrice Rij suivante :
R.(e1)R.(e2)R.(e3)
.e1
.e2Rij
.e3
On a alors la rotation des vecteurs de base qui s'écrit:
R.(ei) = Rji ej, soit R.(ej) = Rij ei (A)
Et la rotation d'un vecteur u=xjej
R.(u) = xj R.(ej), soit : R.(u) = xj Rij ei
Soit, encore, en nommant x
-i les composantes du vecteur R.(u) :
[R.(u)]i = x
-i = Rij xj(B)
On remarque la différence entre les deux équations précédentes (A et B).
Les propriétés classique de cette matrice R sont (car la base est orthonormée): R-1=RT et det(R)=+1
(rotation) ou -1 (symétrie).
Démonstration : c'est une transformation orthogonale donc les angles droits sont conservés :
R.(ei).R.(ej)=δij
Soit (Rki ek).(Rlj el) = δij
Rki Rlj δkl = δij
RTik Rkj = δij
d'où : R-1=RT
D'autre part, le produit vectoriel de deux vecteurs de base donne le troisième (au signe près dans
le cas de certaines transformations, comme les symétries planes), par exemple:
R.(e1)^R.(e2) = ±R.(e3)
Ri1 ei ^ Rj2 ej = ±R3k ek
en explicitant le produit vectoriel : εijk Ri1 Rj2 = ±R3k
On a R.RT=1, d'où, le terme 33 est R3kRTk3=R3kR3k=1, d'où :
εijk R1i R2j R3k = ±1
D'où on identifie directement : det(R)=±1

____________________________________________ page 2 _____________________________________________
1.2 Base canonique des tenseurs du second ordre
On considère un tenseur du second ordre. Par exemple le tenseur des contraintes de Cauchy σ.
Ses composantes σij sont relatives à la base canonique qui est obtenue depuis le produit tensoriel
des tenseur d'ordre 1, i.e. les vecteurs de base ei. Il vient donc :
σ = σij ei ⊗ ej
La base canonique comporte dans 9 composantes ei ⊗ ej. Elle est orthonormée puisque :
(ei ⊗ ej).(ek ⊗ el)=δik δjl
On a l'habitude d'écrire les composantes du tenseur sous forme de matrice 3x3. On peut aussi les
écrire sous forme de ligne ou colonne 1x9 ou 9x1. On peut vérifier que les opérations de contraction
du type σ:ε ou ||σ|| se forment comme sur un vecteur ligne ou colonne habituel dans cette base.
Les composantes s'obtiennent par projection du tenseur sur la base ei ⊗ ej. Cette projection est, au
sens des tenseurs, une contraction sur deux indices. On la note souvent «:», pour généraliser la
notation du produit scalaire sur les vecteurs, qui est une contraction sur un seul indices. D'autres
auteurs la notent «.» aussi.
σij = σ : (ei ⊗ ej)
1.3 Transformation orthogonale des tenseurs du second ordre
La rotation de σ s'obtient aisément :
R.(σ) = σij Rki ek ⊗ Rlj el
D'où la composante kl : (R.(σ))kl = Rki Rlj σij
Ou encore la formule classique (R.(σ))kl = Rki σij RTjl ou l'inverse en prenant P=R-1.
1.4 écriture de Voigt
Vers 1910, le cristallographe Voigt a proposé de simplifier l'écriture en ne rappelant pas les
termes redondants tels que σ23 et σ32 pour les tenseurs symétriques. La notation conventionnelle
est la suivante : -
σ1 = σ11
-
σ2 = σ22
-
σ3 = σ33
-
σ4 = σ23 = σ32
-
σ5 = σ31 = σ13
-
σ6 = σ12 = σ21
Cette notation sous forme de vecteur 1x6 est intéressante pour le calcul analytique et est très
répandue. Toutefois, nous verrons qu'elle n'est pas sans pièges. Nous pouvons déjà constater que le
calcul √ -
σi.-
σi ne correspond pas à la norme de σ, pas plus que le calcul - σi - εi ne correspond à celui
de σ:ε. C'est une source d'erreur fréquente dans le calcul numérique. Nous montrerons plus loin que
l'écriture pour les déformations est : -
ε1 = ε11
-
ε2 = ε22
-
ε3 = ε33
-
ε4 =2 ε23 = 2 ε32
-
ε5 =2 ε31 = 2 ε13
-
ε6 =2 ε12 = 2 ε21
On peut remarquer que 2ε23= γ23, l'écriture ancienne encore utilisée en théorie des poutres pour le
cisaillement.
1.5 Base orthonormée des tenseurs symétriques du second ordre
On forme une base orthonormée des tenseurs symétriques (comme σ ou ε, puisque σ12 = σ21,
etc…) du second ordre comme suit :
(e1 ⊗ e1)

____________________________________________ page 3 _____________________________________________
(e2 ⊗ e2)
(e3 ⊗ e3)
1
√ 2
(e2 ⊗ e3 + e3 ⊗ e2)
1
√ 2
(e3 ⊗ e1 + e1 ⊗ e3)
1
√ 2
(e1 ⊗ e2 + e2 ⊗ e1)
On vérifie aisément que cette base est orthonormée. Les composantes σ
^i du tenseur σ s'obtiennent
de façon habituelle :
σ
^1 = σ:(e1 ⊗ e1)
etc.. jusqu'à :
σ
^6 = σ:1
√ 2
(e1 ⊗ e2 + e2 ⊗ e1)
Les composantes 1,2 et 3 sont les mêmes que celles de l'écriture de Voigt. Cependant les
composantes 4,5 et 6 sont différentes, il vient :
σ
^1 = -
σ1 = σ11
σ
^6 = √ 2 -
σ6 = √ 2 σ12
Cette propriété est souvent décrite comme «le fait de multiplier les termes non diagonaux par √ 2».
En fait, l'existence d'une vraie base de tenseurs permet de conserver les propriétés de norme et de
contraction.
||σ|| = √ σ
^i σ ^i
σ:ε = σ
^i ε ^i
Et, d'autre part, tous les raisonnements de géométrie habituelle (projection, rotation, etc…) sont
valables. Il est important de comprendre qu'il ne s'agit ici pas seulement d'une écriture, mais que l'on
passe de l'espace des tenseurs du second ordre à trois dimensions à l'espace des tenseurs du premier
ordre à 6 dimensions.
1.6 Base hydrostatique, déviatorique
L'élasticité isotrope peut s'écrire très simplement en séparant les parties hydrostatiques et
déviatoriques. Dans les comportements non linéaires, comme en plasticité, on est amené souvent à
distinguer aussi la partie déviatorique (responsable de la plasticité) de la partie hydrostatique (sans
effet). On forme simplement un tenseur hydrostatique normé (invariant par toute rotation) :
H = 1
√ 3
(e1 ⊗ e1 + e2 ⊗ e2 + e3 ⊗ e3)
La composante hydrostatique de la contrainte s'écrit :
σH = σ:H
La composante déviatorique est le complément de σ sur σH :
σD = σ - σH
L'espace des tenseurs symétrique du second ordre se scinde en deux sous espaces, hydrostatique et
déviatoriques (espaces isotropes). Une loi d'élasticité isotrope postule que contrainte et déformation
sont coaxiaux (proportionnels) dans chacun de ces sous espaces :
σH = 3K εH
σD = 2µ εD
Exercice : en identifiant cette écriture sur la loi d'élasticité traditionnelle qui s'écrit :
ε = 1+ν
E σ - ν E tr(σ) I

____________________________________________ page 4 _____________________________________________
reconnaitre que K est le module de compressibilité hydrostatique et que µ est le module de
cisaillement du matériau. On verra aussi plus tard que ce sont les deux modules de Kelvin, ou valeurs
propres du tenseur d'élasticité. On rappelle enfin l'écriture de Lamé :
σ = 2µε + λtr(ε)I
Comme il n'y a que deux constantes d'élasticité isotrope indépendantes, on rappelle les relations
entre les modules d'Young E et de Poisson ν, compressibilité hydrostatique K et coefficient de Lamé
λ etµ :
(E,ν) (K,µ)(λ,µ)S, n
E module
d'Young E = 9 K µ
3 K + µE = µ 3λ + 2µ λ + µE(n) = 1
n.n.S.n.n
ν coefficient de
Poisson ν = 3 K - 2 µ
2 (3 K + µ)ν = λ
2 (λ + µ)
ν (m,n) =
−m.m.S.n.n
n.n.S.n.n
K module de
compressibilité K = E
3 (1 - 2 ν)K = 3λ+2µ
3K = 1
Siikk
µ module de
cisaillement µ = E 2(1 + ν)µ(m,n) = 1
8 m.n.S.n.m
λ coefficeient de
Lamé λ = νE
(1 + ν) (1 - 2 ν)λ=3K-2µ 3
2) Tenseur d'élasticité
2.1 Définition
On est en élasticité linéaire si le tenseur des contraintes est linéaire par rapport à celui des
déformations. La loi linéaire la plus générale s'écrit donc :
σ = C:ε
Ou, en base canonique : σij = Cijkl εkl
En écriture de Voigt : σ
-i = C
-
ij.ε
-j
En base de tenseurs : σ
^i = C
^ij.ε
^j
Le tenseur d'élasticité s'écrit donc sous forme de table 6x6, ce qui illustre bien sa nature de tenseur
du second ordre dans l'espace à 6 dimensions. E
2.2 Symétries indicielles
Le tenseur d'élasticité est un tenseur du quatrième ordre. Il possède a priori 34=81
composantes indépendantes. Toutefois comme ε est symétrique, il vient σij = Cijkl εlk et, en
permutant les indices muets : σij = Cijlk εkl. Cette relation, valable pour tout ε fournit la petite
symétrie de C.
Cijkl = Cijlk
Un raisonnement analogue sur σ conduit à la seconde relation de petite symétrie :
Cijkl = Cjikl
Le premier principe de la thermodynamique fournit la grande symétrie indicielle :
Cijkl = Cklij
Démonstration (utilise la thermodynamique) : on considère une transformation réversible
(élastique) quasistatique (dec=0) et adiabatique (δqe=0).

____________________________________________ page 5 _____________________________________________
Le th. de l'énergie cinétique : dec = δwi + δwe
0 = -σ:dε + δwe
Le 1er ppe : du + dec = δwe + δqe
du = σ:dε + 0
σ et ε sont des variables d'état :
σ = ∂u
∂ε
la loi de comportement élastique donne : C =
∂σ
∂ε
D'où C = ∂2u
∂ε⊗∂ε soit Cijkl = ∂2u ∂εij∂εkl = ∂2u ∂εkl∂εij
Ce qui entraîne la relation de grande symétrie Cijkl = Cklij.
L'ensemble de ces relations permet de réduire le nombre de composantes indépendantes du tenseur
d'élasticité à 21. Le compte est aisé à partir de l'écriture en base de tenseurs (respectivement en
écriture de Voigt), puisque la table 6x6, C
^ij (respectivement C
-
ij), qui représente C est alors
symétrique. Le nombre de composantes indépendantes est alors calculable ligne par ligne :
6+5+4+3+2+1=21.
Au niveau de la notation de Voigt, la convention est simplement la correspondance terme à terme
avec la base canonique ; il vient :
C
-
11 = (e1 ⊗ e1):C:(e1 ⊗ e1) = C1111
C
-
14 = (e1 ⊗ e1):C:(e2 ⊗ e3) = C1123
C
-
44 = (e2 ⊗ e3):C:(e2 ⊗ e3) = C2323
Remarque, on peut aussi écrire la projection dans la base des tenseurs du quatrième ordre, ce qui
donne un écriture du type suivant, équivalente mais un peu lourde :
C
-
11 = C::(e1 ⊗ e1 ⊗ e1 ⊗ e1) = C1111
Les composantes en base de tenseurs C
^ij se calculent de la manière habituelle par projection sur les
éléments de la base, par exemple :
C
^11 = (e1 ⊗ e1):C:(e1 ⊗ e1) = C1111
C
^14 = (e1 ⊗ e1):C:1
√ 2
(e2 ⊗ e3 + e3 ⊗ e2) = C
^41 = √ 2 C1123
C
^44 = 1
√ 2
(e2 ⊗ e3 + e3 ⊗ e2):C:1
√ 2
(e2 ⊗ e3 + e3 ⊗ e2) = 2 C2323
Au final, la relation d'élasticité s'écrit de la manière suivante en écriture de Voigt, en fonction des
termes en base canonique :