traitment du signal

SOMMAIRE
INTRODUCTION GÉNÉRALE
I- CLASSIFICATION DES SIGNAUX
PROBABILITÉS ET PROCESSUS STOCKASTIQUES
II- REPRÉSENTATION VECTORIELLE DES SIGNAUX
SÉRIE DE FOURIER
TRANSFORMÉE DE FOURIER
TRANSFORMÉE DE LAPLACE
III- ECHANTILLONNAGE ET THÉORÈME DE SHANNON
TRANSFORMÉE DE FOURIER DISCRÊTE TFD-DFT
TRANSFORMÉE DE FOURIER RAPIDE TFR-FFT
TRANSFORMÉE EN Z
IV- LES FILTRES NUMÉRIQUES
FILTRES A RÉPONSE IMPULSIONNELLE FINIE (RIF)
FILTRES A RÉPONSE IMPULSIONNELLE INFINIE (RII)
BIBLIOGRAPHIE
ANNEXE

INTRODUCTION GÉNÉRALE
Le mot Signal est issu du mot - signum en latin - qui dénote un objet, une marque, un élément de
langage, un symbole convenu pour servir à une information. Personne ne peu nier que l'usage des
signes remonte à la préhistoire.
Donc, un signal est une source d'information, il peut contenir l'information et le bruit. Le traitement se
fait dans le but d'améliorer ou de séparer l'information des choses indésirables.
La théorie de traitement du signal : touche à tous les secteurs dans les quels l'information est perçue
par l'intermédiaire d'observations expérimentales de grandeurs mesurables. La théorie du signal est
largement liée à la perception et le traitement. Ce lien étroit indique pourquoi cette discipline s'est
avant tous développée en relation avec les applications de l'électricité et plus particulièrement celle de
la métrologie responsable de la perception, des télécommunications et de l'informatique chargé du
traitement.
Donc, parmi les principaux objectifs du traitement du signal, il y a la détection et l'interprétation des
signaux porteurs de l'information. "Signal Processing". Cette discipline trouve son champ
d'application dans tous les domaines concernés par la perception, la transmission et l'exploitation de
l'information. Ce vaste champ s'étant des télécommunications à l'instrumentation scientifique, de
l'automatisation industrielle au génie biomédicale en passant par le traitement d'image la
reconnaissance des formes, la robotique, l'intelligence artificielle.
Instrumentation Scientifique
Intelligence Artificielle Télécommunication
Traitement d'images
Reconnaissance
de formes
Automatisation Industrielle
Les premières applications de cette science ont vu le jours au 19ème siècle lors de l'apparition de
l'exploitation des signaux électriques avec l'arrivée du télégraphe (Morse Cooke wheastone (1830-
40)) qui a été suivi par le téléphone (Bell 1876) en suite la radio Papov, Marconi (1895-1896).
Traitement du Signal 12-13 2
Traitement du
Signal
Détection
Interprétation
Robotique

L'invention du transistor, en 1948, suivie environ 10 ans plus tard par la mise au point de la
technologie des circuits intégrés, allaient permettre la réalisation des systèmes de traitement complexe
et la diversification des champs d'applications. Les années 90 ont vu la naissance des processurs de
traitement du signal permettant de nouvelles applications particuliérement les applications en temps
réel.
I- Définitions
1- Définition d'un signal
Un signal est la représentation physique de l'information qu'il convoie de sa source à son
destinataire (généralement courant ou tension).
2- Définition du bruit
On appelle bruit (noise) tout phénomène perturbateur (interférence, bruit de fond etc. ...) gênant la
perception ou l'interprétation de l'information contenue dans un signal.
3- Définition Rapport signal bruit
C'est une mesure du degré de contamination du signal par le bruit, il s'exprime sous la forme du
rapport  des puissances respectives du signal Ps et du bruit Pb.
PP
s
b
P x t dt
x
( )
2
db
10
10
log ( )
N.B: Ce qui différencie le signal du bruit est avant tout l'intérêt de l'observateur. Exemple: Certains
phénomènes électromagnétiques d'origine galactique captés par des antennes sont considérées
comme du bruit par les ingénieurs des télécommunications et comme un signal de plus haut intérêt
par les radioastronomes.
- Exemples de signaux
Le modèle mathématique d'un signal est une fonction de une, parfois deux, voire même trois
variables s(t), i(x,y) i(x,y,t).
Signal microphonique Signal de vibration machine tournante
s(t) le cas le plus courant, la variable t est usuellement le temps mais il peut être une distance par
exemple.
Traitement du Signal 12-13 3
s(t)
t
s(t)
t

i(x, y) signaux bidimensionnels, ce sont généralement des fonctions de coordonnées spatiales, le
plus couramment des images.
i(x, y, t) signaux tridimensionnels, ce sont généralement des fonctions de coordonnées spatiales,
le plus couramment des scènes d'images.
Exemple : signal représentant la vibration d’une machine
Vibration d’une machine en fonction du temps ‘mesure prise dans les laboratoires de la FST-BM’
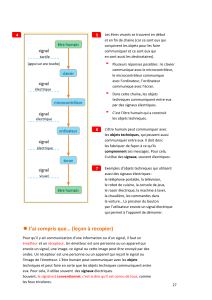
Exemple : La Communication
Cet exemple, illustre une chaîne de transmission dans laquelle le bruit s'ajoute au signal au niveau
du codage (émetteur) puis dans le canal de transmission (rayonnement, couplage). Afin de pouvoir
exploiter convenablement l'information transmise, il est nécessaire de faire du traitement du signal au
niveau de la réception pour extraire notre signal utile du bruit.
4- Définition d'un système
Traitement du Signal 12-13 4
x
y
i(x,y)
i(x,y,t1)
i(x,y,t2)
i(x,y,t3)
Amplitude
(mm)

Un système est un ensemble d'objets liés entre eux dans le but de réaliser une tâche. Ce
dispositif est soumis aux lois physiques est caractérisé par des grandeurs de deux types d'entrée (ou
excitation) et la sortie.
Où x(t) est l'entrée ou l'excitation, y(t) est la sortie et h(t) est la réponse impulsionnelle, c'est la sortie
du système lorsqu'il est excité par (t) Dirac
Ces signaux d'entrée et de sortie sont respectivement notés x(t) et y(t). Par exemple y(t)=x2(t)
désigne la sortie d'un dispositif non linéaire quadrature dont la caractéristique est définie par y=x2.
a- Système linéaire
Si x1(t) donne comme sortie y1(t)
x2(t) donne comme sortie y2(t)
Dans le cas d'un système linéaire :
a x1(t) + b x2(t) a y1(t) + b y2(t)
Système non linéaire
b- Système invariant Stationnaire
x(t) y(t)
x(t- t1) y(t- t1)
Les mêmes causes produisent les mêmes effets.
c- Systèmes causal
h(t) = 0 pour t < 0
l'effet ne peut pas précéder la cause (considération physique).
d- Système stable
Si on supprime la cause ou finit par supprimer l'effet.
Dans un premier temps notre étude portera sur les SLIT. "Système Linéaire Invariant dans le Temps"
5- Définition d'une fonctionnelle
Une fonctionnelle est une fonction de fonctions, les signaux résultant d'un traitement ou certains
de leurs paramètres sont souvent exprimés par des relations fonctionnelles.
Traitement du Signal 12-13 5
x(t) y(t)
h(t)
x(t)
t
y(t)
t
x(t-t1)y(t-t1)
tt
t1t1