chapter-3-synchronous-motors

Studocu is not sponsored or endorsed by any college or university
Chapter 3 - Synchronous Motors
ELECTRICAL POWER SYSTEMS AND MACHINES (University of Sunderland)
Studocu is not sponsored or endorsed by any college or university
Chapter 3 - Synchronous Motors
ELECTRICAL POWER SYSTEMS AND MACHINES (University of Sunderland)
Downloaded by Tarak BENSLIMANE ([email protected])
lOMoARcPSD|6847370

EEE4323 Electrical Machines – Synchronous Motors
Chapter 3: Synchronous Motors
Synchronous motors are synchronous machines used to convert
electrical power to mechanical power.
This chapter explores the basic operation of synchronous motors
and relates their behaviour to that of synchronous generators.
I. Basic principles of motor operation
How does it work?
The rotor field current IF produces a steady-state magnetic
field
BR
.
A three-phase set of voltages applied to the stator produces
a three-phase current flow in the winding.
These currents then produce a uniform rotating magnetic
field
BS
.
Since there are two magnetic fields in the machine,
BR
tends to line up with
BS
.
Since
BS
is rotating by a difference of ,
BR
will
constantly try to catch up.
The amount of torque depends on the angle between the two
magnetic fields.
Just like in the induction motor, the rotor “chases” the rotating
BS
in a circle but never quite catching up with it.
_____________________________________________________________________
1
Updated March 2011
Downloaded by Tarak BENSLIMANE ([email protected])
lOMoARcPSD|6847370

EEE4323 Electrical Machines – Synchronous Motors
Since a synchronous motor is the same physical machine as a
synchronous generator, all the basic speed, power and torque
equations applies to the motor as well.
The only difference is the direction of power flow, which is
opposite/ reverse.
The equivalent circuit of a synchronous motor:
Since direction of power flow is reversed, the direction of
current flow in the stator of the motor is expected to reverse
also.
Hence, the equivalent circuit of the synchronous motor is
exactly the same as that of the generator except: the reference
direction of IA is reversed.
The full and per-phase equivalent circuit is shown below:
_____________________________________________________________________
2
Updated March 2011
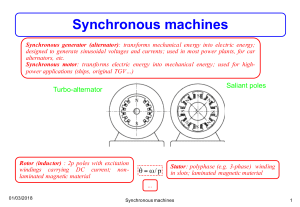
A two-pole
synchronous motor.
Downloaded by Tarak BENSLIMANE ([email protected])
lOMoARcPSD|6847370

EEE4323 Electrical Machines – Synchronous Motors
Remember: the three phases of the equivalent circuit may be
either Y- or ∆- connected.
Due to the change in direction of IA, the voltage equation for the
armature circuit yields:
VφEAjX SIARAIA
(6.1)
Or
EAVφjXSIARAIA
(6.2)
This is exactly the same equation for a generator except the sign
on the current term is reversed.
The synchronous motor from a magnetic field perspective:
Synchronous Motor Synchronous Generator
Phasor Diagram: Phasor Diagram:
_____________________________________________________________________
3
Updated March 2011
Downloaded by Tarak BENSLIMANE ([email protected])
lOMoARcPSD|6847370

EEE4323 Electrical Machines – Synchronous Motors
Magnetic field diagram: Magnetic field diagram:
Direction of induced torque is
____________ the direction of
motion.
Direction of induced torque is
____________ the direction of
motion.
Synchronous Motor Synchronous Generator
EA lies __________ VФ.EA lies __________ VФ.
BR lies __________ Bnet.BR lies __________ Bnet.
jXSIA points from EA to VФ. jXSIA points from VФ to EA.
6.2 Steady State Synchronous Motor Operation
As with the synchronous generator, the behaviour of
synchronous motors varies with varying conditions of load and
field current.
In the following discussion, the armature resistance RA will
generally be ignored for simplicity. However, it may be included
in some of the numerical calculations.
_____________________________________________________________________
4
Updated March 2011
Downloaded by Tarak BENSLIMANE ([email protected])
lOMoARcPSD|6847370