Arithmétique, PGCD

Troisième DEMONSTRATIONS – Arithmétique
Séquence 1 : division euclidienne
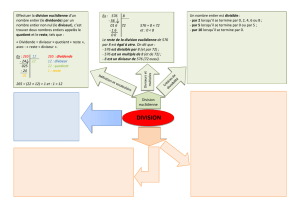
Définition du quotient et du reste d’une division euclidienne
Soient et deux nombres entiers naturels, ≠ 0. Poser la division euclidienne de 
par c’est trouver deux entiers naturels  et tels que : =×+, avec
<
0
r b
.
On dit que est le quotient de cette division, et le reste.
Attention
•La condition
<
0
r b
est très importante ! Par exemple si l’on souhaite
obtenir la division euclidienne de 22 par 3, l’écriture : 22 = 3 × 5 + 7 ne
traduit pas cette division euclidienne car
<
0 7 3
.
•On ne peut poser la division que par un nombre entier naturel non nul.
Séquence 2 : être un diviseur, être un multiple
Soient ∈ ℕ ,∈ ℕ∗. On dit que est un diviseur de , ou que est un multiple de 
le reste  de la division euclidienne de par est nul.
        °1
Cherchons la division euclidienne de 32 par 5 s’écrit : il s’agit de trouver deux entiers
naturels et tels que : 32 = 5 × +, avec
<
0 5
r.
Comme on a : 32 = 5 × 6 + 2, avec 0 2 < 5, on en déduit que le quotient est = 6
et le reste est = 2. Notons que c’est le       qui doit être « petit » puisqu’il doit
obéir à la contrainte « être strictement plus petit que le nombre par lequel on divise »,
mais le quotient peut parfois, comme dans notre exemple, être plus grand que .
Comme le reste de cette division n’est pas nul, le nombre 5n’est pas un diviseur de 32,
ou ce qui revient au même : 32 n’est pas un multiple de 5.
        °2
Cherchons la division euclidienne de 21 par 3: il s’agit de trouver deux entiers
naturels et tels que : 21 = 3 × +, avec 0 < 3.
Comme on a : 21 = 3 × 7 + 0, avec 0 0 < 3, on en déduit que le quotient est = 7
et le reste est = 0.
Comme le reste de cette division est nul, le nombre 3est un diviseur de 21, ou ce qui
revient au même : 21 est un multiple de 3.
      éé
Soient ∈ ℕ, ∈ ℕ∗:
 est un diviseur de  il existe ∈ ℕ tel que =×
 est un multiple de  il existe ∈ ℕ tel que =×
 Preuve
Les deux énoncés étant équivalents, montrons simplement la première assertion.
Montrons que :
« si  est un diviseur de alors il existe ∈ ℕ tel que =×».
Soit est un diviseur de : par définition « d’être un diviseur », on en déduit que le
reste de la division euclidienne de par est nul : =×+ 0=×.
Il existe donc effectivement ∈ ℕ tel que =×, à savoir =.
Montrons que :
« s’il existe ∈ ℕ tel que =×, alors est un diviseur de ».
 =×=×+ 0 ; cette dernière égalité traduit la division euclidienne de 
par avec un reste nul, et par définition de « être un diviseur », on en déduit que est
un diviseur de .
L’égalité 45 = 15 × 3 montre que 15 est un diviseur de 45 ou de façon équivalente que
45 est un multiple de 15.
Remarquons que l’égalité 45 = 15 × 3 s’écrit aussi 45 = 3 × 15 et donc 3est un
diviseur de 45 et 45 est un multiple de 3.
i. Le nombre 1est un diviseur de n’importe quel nombre entier naturel.
ii. Tout nombre entier non nul est un diviseur de 0.
iii. Tout nombre entier non nul est un diviseur de lui-même.
preuve
i. Soit ∈ ℕ, on a : = 1 × , donc il existe ∈ ℕ tel que = 1 × , à
savoir =, ce qui montre que 1est un diviseur de .
ii. Soit ∈ ℕ∗, on a : 0 = × 0, donc il existe ∈ ℕ tel que 0 = ×, à
savoir = 0, ce qui montre que : est un diviseur de 0.
MathsEnClair.com - Tous droits réservés

iii. Soit ∈ ℕ∗, on a : =× 1, donc il existe ∈ ℕ tel que =×, à
savoir = 1, ce qui montre que : est un diviseur de . Remarquons que
l’on exige ≠ 0 puisque on ne peut diviser que par un entier naturel ≠ 0.
      éé
Les diviseurs d’un entier naturel non nul sont nécessairement tous inférieurs ou égaux à
ce nombre.
 preuve
Soit ∈ ℕ∗:∈ ℕ∗est diviseur de il existe ∈ ℕ tel que =×. Il est
impossible que = 0, car alors =×=× 0 = 0 ce qui contredit ∈ ℕ∗.
On a donc : =×avec ≠, donc il faut multiplier par un nombre plus grand
ou égal à 1 pour obtenir , ce qui montre bien que est inférieur ou égal à .
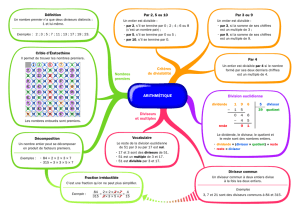
Séquence 3 : définition du PGCD
Définition
Soient et deux entiers naturels non nuls. Dans la liste des diviseurs en communs, il
y en a un qui et le plus grand : il s’appelle PGCD des deux entiers de départ.
 Preuve
Soient ∈ ℕ∗et ∈ ℕ∗.
La liste des diviseurs communs contient au moins le nombre 1donc elle n’est pas vide.
Un diviseur de ≠ 0 lui est nécessairement inférieur ou égal, et de même pour le
diviseurs de ≠ 0, si bien qu’un diviseur commun de et est inférieur ou égal au
minimum de ces deux nombres.
La liste des diviseurs communs est non vide, est formée de nombre entiers, et est
majorée par le plus petit des deux nombres et donc elle est constituée d’un nombre
fini d’éléments : le plus grand d’entre eux existe donc bien. 
Diviseurs de 20 : 1 − 2 − 4 − 5 − 10 − 20.
Diviseurs de 30 : 1 − 2 − 3 − 5 − 6 − 10 − 15 − 30.
La liste des diviseurs en commun est : 1 − 2 − 5 − 10. Comme le plus grand élément
de la liste des diviseurs en commun est 10, on en déduit que     (20 ; 30)= 10.
      éé
Soient et deux entiers naturels non nuls :
i.     ( ;)=
ii.                    ,      ç  é                           
     :    ( ;)=
i.  est un diviseur de lui-même, et comme ≠ 0 il n’admet pas de diviseur qui
soit plus grand que lui, donc le plus grand diviseur de et de lui-même est .
ii. D’une part : on sait déjà que     ( ;)est inférieur ou égal au minimum de
ces deux nombres. Comme est un multiple non nul de , il est supérieur ou
égal à , donc le minimum de et est , et par conséquent     ( ;) .
D’autre part :  est un diviseur de lui-même, et par hypothèse c’est un diviseur
de , donc est un diviseur commun de et , et comme le     est le plus
grand diviseur commun de et , on en déduit :      ( ;).
Conclusion :     ( ;) et      ( ;)donc : =    ( ;).
Séquence 4 : PGCD Algorithme des différences
Propriété de la soustraction
Soient ∈ ℕ∗et ∈ ℕ∗,>, alors :     ( ;)=    ( ;−).
Cette égalité signifie que :                  =    (     ;     −     )
Il suffit de montrer que la liste des diviseurs communs de   et est la même que la
liste des diviseurs communs de et −.
Première partie
Soit un diviseur commun de et : il existe ∈ ℕ∗et ∈ ℕ∗tels que =×et
=×. Remarquons que comme >, on a : >.
On a alors : −=×−× −=×(−). La différence de deux
entiers est un entier donc (−)∈ ℕ, l’égalité −=×(−)montre que est
un diviseur de −.
Résumons : tout diviseur commun de et est aussi un diviseur commun de et
−.
MathsEnClair.com - Tous droits réservés

Deuxième partie
Soit un diviseur commun de et −: il existe ∈ ℕ∗et ∈ ℕ∗tels que
=×et −=×. On a donc : +(−)=×+×
=×(+).Comme +∈ ℕ∗, la dernière égalité montre que ′est un
diviseur de . Comme ′est un diviseur de et est un diviseur de donc c’est un
diviseur commun de et .
Résumons : tout diviseur commun de et −est un diviseur commun de et .
Synthèse
La liste des diviseurs communs de  et est la même que la liste des diviseurs
communs de et −donc ces deux listes ont le même plus grand élément, ce qui
s’écrit :     ( ;)=    ( ;−)
La propriété de la soustraction est la justification de l’algorithme des soustractions
successives permettant de calculer le     de deux entiers non nuls.
Séquence 5 : PGCD Algorithme des divisions euclidiennes
Propriété du reste de la division euclidienne
Soient ∈ ℕ∗et ∈ ℕ∗,>, et le reste de la division euclidienne de  par ,
alors :     ( ;)=    ( ;). Cette égalité signifie que :
                 =    (     ;                            ).
est le reste de la division euclidienne de par donc il existe ∈ ℕ tel que :
=  +=−  .
Première partie : montrons que « tout diviseur commun de et est aussi un diviseur
commun de et ».
Soit un diviseur commun de et de : il existe ∈ ℕ et ∈ ℕ tels que : =×
et =×′.
Comme : =−  , on en déduit : =×−××=×(−).
Comme le produit et la différence de deux entiers relatifs sont des entiers relatifs, on en
déduit que −est un entier relatif. De plus est positif ou nul et est positif, donc
−est positif. Le nombre −est entier et positif ou nul, donc c’est un entier
naturel. L’égalité : =×(−)montre que est un diviseur de .
On sait que  est un diviseur de et est un diviseur de donc c’est un diviseur
commun de et .
Résumons : tout diviseur commun de et est aussi un diviseur commun de et .
2ième partie : montrons que « tout diviseur commun de et est aussi un diviseur commun de
et ».
Soit ′un diviseur commun de et de ; il existe ′′ ∈ ℕ et    ∈ ℕ tels que :
=′ × ′′ et =′ × ′′′.
Comme =  +, on en déduit : =′ ×   ×+′ × ′′′
=′ × (  ×+   ), qui montre que ′est un diviseur de .
On sait que ’est un diviseur de et de donc c’est un diviseur commun de et .
Résumons : tout diviseur commun de et est aussi un diviseur commun de et .
La liste des diviseurs communs de  et est la même que la liste des diviseurs
communs de et donc ces deux listes ont le même plus grand élément, ce qui s’écrit :
      ;  =    (;)
La propriété du reste de la division euclidienne est la justification de l’algorithme des
divisions successives, aussi appelé algorithme d’Euclide, permettant de calculer le
    de deux entiers non nuls.
Séquence 6 : applications du PGCD
Définition de « premiers entre eux »
Par définition : ∈ ℕ∗et ∈ ℕ∗sont premiers entre eux     ( ;)= 1.
Ce qui signifie :
deux entiers naturels non nuls sont premiers entre eux lorsque leur     vaut 1.
Attention à ne pas confondre la notion « premiers entre eux », qui est une relation entre deux
entiers naturels non nuls, avec la notion « être un nombre premier » qui est une notion de nature,
donc une notion ne portant que sur un seul nombre.
Complément hors programme en troisième : par définition on dit qu’ un entier naturel est premier
lorsqu’il admet exactement deux diviseurs. Ces deux diviseurs sont alors 1et le nombre lui-même.
•5 est un nombre premier ( deux diviseurs exactement : 1et 5 )
•9 n’est pas premier ( trois diviseurs : 1, 3, 9 )
•2 est premier ( deux diviseurs : 1 et 2 )
•1 n’est pas premier ( un seul diviseur : 1)
MathsEnClair.com - Tous droits réservés

Fraction irréductible : définition
Soit ∈ ℕ∗et ∈ ℕ∗. Par définition, la fraction 
est irréductible     ( ;)= 1.
Propriété de non simplification d’une fraction irréductible
La fraction est irréductible La fraction est sous sa forme simplifiée au maximum.
 preuve
Première partie : montrons que « si
a
b
est irréductible, alors elle est simplifiée au
maximum ».
Soit
a
b
une fraction irréductible donc par définition d’une fraction irréductible :
    ( ;)= 1.
◊Supposons que la fraction 
est simplifiable : il existe alors entier supérieur ou égal
à2,∈ ℕ∗,∈ ℕ∗tels que =×′et =×′. Ces deux égalités impliquent
que est un diviseur commun de et .
Le     étant le plus grand des diviseurs communs de et , on a :     ( ;) .
Comme  2, on en déduit :     ( ;) 2, ce qui est impossible puisque
    ( ;)= 1. Par conséquent la supposition de départ ◊doit être rejetée et donc on
peut affirmer que la fraction
a
b
n’est pas simplifiable.
Deuxième partie : montrons que « si
a
b
est simplifiée au maximum, alors
a
b
est
irréductible ».
Soit
a
b
une fraction simplifiée au maximum.
◊Supposons     ( ;)≠ 1, alors     ( ;) 2, et il existe   et ′tels que :
=    ( ;)×et =    ( ;)×′.
On alors :
×
=
×
( ; )
( ; ) '
a PGCD a b k
b PGCD a b k
, et par conséquent une simplification par     ( ;)
qui est un nombre supérieur ou égal à 2 serait possible, ce qui est contradictoire avec
«
a
b
est simplifiée au maximum ». Par conséquent la supposition de départ ◊doit être
rejetée, donc     ( ;)= 1 : la fraction
a
b
est irréductible. 
Règle de simplification des fractions **
Si l’on simplifie une fraction par le     de son numérateur et dénominateur, alors on
obtient la fraction irréductible qui lui est égale.
 Preuve
Soit ∈ ℕ∗et ∈ ℕ∗, et considérons la fraction
a
b
.
1     ∶    ( ;)= 1
On a alors :
=÷    ( ;) ÷    ( ;)=÷ 1 ÷ 1 =
Comme
a
b
est irréductible, la simplification par     ( ;), qui ici n’a aucun effet,
donne bien la forme irréductible.
2è     ∶    ( ;)≠ 1
Il faut montrer que :
(1) la fraction
a
b
est simplifiable par     ( ;)
(2) la fraction obtenue après simplification par le     ( ;)est irréductible.
Montrons (1)
Le     ( ;)est le plus grand diviseur commun de et , donc c’est un diviseur
commun de et donc il existe ∈ ℕ∗et ∈ ℕ∗tels que : =    ( ;)×et
=    ( ;)×′.
On a alors :
=    ( ;)×     ( ;)×=
Soit finalement
=
'
a k
b k
, et comme et ′sont des nombres entiers,
'
k
k
est bien une
fraction, égale à la fraction
a
b
de départ.
MathsEnClair.com - Tous droits réservés

(2) Montrons que la fraction
'
k
k
est irréductible.
Supposons que la fraction
'
k
k
ne soit pas irréductible, c’est-à-dire que :
    ( ;)≠ 1, alors     ( ;) 2.
Il existe ∈ ℕ∗et ∈ ℕ∗tels que =    ( ;)×et =    ( ;)×′.
On a : =    ( ;)×=    ( ;)×    ( ;)×et
=    ( ;)×′ =     ( ;)×    ( ;)×′.
Ces deux égalités montrent que     ( ;)×    ( ;)est un diviseur commun
de et , et comme     ( ;) 2, ce nombre est strictement supérieur à
    ( ;)ce qui est absurde puisque     ( ;)est le plus grand des divieurs
communs de et .
La supposition de départ abouti à une chose absurde, donc elle doit être rejetée et par
conséquent il est certain que la fraction
'
k
k
est irréductible. 
MathsEnClair.com - Tous droits réservés