Microelectronis such a good things

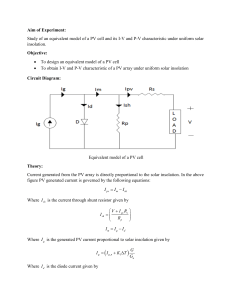
G. Rizzoni, Principles and Applications of Electrical Engineering, 6th Edition Problem solutions, Chapter 2
2.1
PROPRIETARY MATERIAL. © The McGraw-Hill Companies, Inc. Limited distribution permitted only to teachers and
educators for course preparation. If you are a student using this Manual, you are using it without permission.
Chapter 2: Fundamentals of Electrical Circuits – Instructor Notes
Chapter 2 develops the foundations for the first part of the book. Coverage of the entire chapter would be
typical in an introductory course. The first four sections provide the basic definitions (Section 2.1) and cover
Kirchoff’s Laws and the passive sign convention (Sections 2.2, 2.3 And 2.4); A special feature, Focus on
Methodology: The Passive Sign Convention (p. 39) and two examples illustrate this very important topic. A second
feature, that will recur throughout the first six chapters, is presented in the form of sidebars. Make The Connection:
Mechanical Analog of Voltage Sources (p. 24) and Make The Connection: Hydraulic Analog of Current Sources (p.
26) present the concept of analogies between electrical and other physical domains.
Sections 2.5and 2.6 introduce the i-v characteristic and the resistance element. Tables 2.1 and 2.2 on p. 45
summarize the resistivity of common materials and standard resistor values; Table 2.3 on p. 48 provides the
resistance of copper wire for various gauges. The sidebar Make The Connection: Electric Circuit Analog of
Hydraulic Systems – Fluid Resistance (p. 44) continues the electric-hydraulic system analogy.
Finally, Sections 2.7 and 2.8 introduce some basic but important concepts related to ideal and non-ideal
current sources, and measuring instruments. In the context of measuring instruments, Chapter 2 introduces a third
feature of this book, the Focus on Measurements boxes, referenced in the next paragraph.
The Instructor will find that although the material in Chapter 2 is quite basic, it is possible to give an
applied flavor to the subject matter by emphasizing a few selected topics in the examples presented in class. In
particular, a lecture could be devoted to resistance devices, including the resistive displacement transducer of Focus
on Measurements: Resistive throttle position sensor (pp. 56-59), the resistance strain gauges of Focus on
Measurements: Resistance strain gauges (pp. 58-59),and Focus on Measurements: The Wheatstone bridge and force
measurements (pp. 59-60). The instructor wishing to gain a more in-depth understanding of resistance strain gauges
will find a detailed analysis in the references1.
Early motivation for the application of circuit analysis to problems of practical interest to the non-electrical
engineer can be found in the Focus on Measurements: The Wheatstone bridge and force measurements. The
Wheatstone bridge material can also serve as an introduction to a laboratory experiment on strain gauges and the
measurement of force (see, for example2). Finally, the material on practical measuring instruments in Section2.8b
can also motivate a number of useful examples.
The homework problems include a variety of practical examples, with emphasis on instrumentation.
Problem 2.51 illustrates analysis related to fuses; problems 2.65 relates to wire gauges; problem 2.70 discusses the
thermistor; problems 2.71 discusses moving coil meters; problems 2.79 and 2.80 illustrate calculations related to
strain gauge bridges; a variety of problems related to practical measuring devices are also included in the last section.
The 5th Edition of this book includes 26 new problems; some of the 4th Edition problems were removed, increasing
the end-of-chapter problem count from 66 to 80.
It has been the author's experience that providing the students with an early introduction to practical
applications of electrical engineering to their own disciplines can increase the interest level in the course
significantly.
1 E. O. Doebelin, Measurement Systems – Application and Design, 4th Edition, McGraw-Hill, New York, 1990.
2 G. Rizzoni, A Practical Introduction to Electronic Instrumentation, 3rd Edition, Kendall-Hunt, 1998.
Learning Objectives for Chapter 2
1. Identify the principal elements of electrical circuits: nodes, loops, meshes, branches, and voltage
and current sources.
2. Apply Kirchhoff’s Laws to simple electrical circuits and derive the basic circuit equations.
3. Apply the passive sign convention and compute power dissipated by circuit elements.
4. Apply the voltage and current divider laws to calculate unknown variables in simple series,
parallel and series-parallel circuits.
5. Understand the rules for connecting electrical measuring instruments to electrical circuits for the
measurement of voltage, current, and power.

G. Rizzoni, Principles and Applications of Electrical Engineering, 6th Edition Problem solutions, Chapter 2
2.2
PROPRIETARY MATERIAL. © The McGraw-Hill Companies, Inc. Limited distribution permitted only to teachers and
educators for course preparation. If you are a student using this Manual, you are using it without permission.
Section 2.1: Definitions
Problem 2.1
An isolated free electron is traveling through an electric field from some initial point where its coulombic potential
energy per unit charge (voltage) is 17 kJ/C and velocity = 93 Mm/s to some final point where its coulombic potential
energy per unit charge is 6 kJ/C. Determine the change in velocity of the electron. Neglect gravitational forces.
Solution:
Known quantities:
Initial Coulombic potential energy,
Vi=17kJ /C
; initial velocity,
Ui=93Mm
s
; final Coulombic potential energy,
V
f
=6kJ /C
.
Find:
The change in velocity of the electron.
Assumptions:
∆PE
g
<< ∆PE
c
∆KE = −∆PE
c
)()(
2
122 ifeife VVqUUm −−=−
( )
( )
2
2
15
2
2
15
31
19
2
22
10864.310649.8
176
1011.9 106.12
93
)(
2
s
m
s
m
kVkV
kg
C
s
m
M
VV
m
q
UU
if
e
e
if
×−×=
−
×
×−
−
=
−−=
−
Uf=6.917×107m
s
U
f
−U
i
=93 Mm
s−69.17 Mm s=23.83 Mm s.

G. Rizzoni, Principles and Applications of Electrical Engineering, 6th Edition Problem solutions, Chapter 2
2.3
PROPRIETARY MATERIAL. © The McGraw-Hill Companies, Inc. Limited distribution permitted only to teachers and
educators for course preparation. If you are a student using this Manual, you are using it without permission.
Problem 2.2
The unit used for voltage is the volt, for current the ampere, and for resistance the ohm. Using the definitions of
voltage, current, and resistance, express each quantity in fundamental MKS units.
Solution:
Known quantities:
MKSQ units.
Find:
Equivalent units of volt, ampere and ohm.
Analysis:
sJ
C
CsJ
s
C
A
C
J
V
⋅
=
==
⋅
=
×
==
=
==
=
==
=
2
22
Volt
Ampere
Siemense
Conductanc
Coulomb
secondJoule
Ampere
Volt
Ohm
Resistance
second
Coulomb
AmpereCurrent
Coulomb
Joule
VoltVoltage
Problem 2.3
A battery can deliver 2.7 · 106 coulombs of charge. Find the capacity and delivered electrons of the battery.
Solution:
Known quantities:
qBattery = 2.7 · 106 C.
Find:
a) The current capacity of the battery in ampere-hours
b) The number of electrons that can be delivered.
Analysis:
a) There are 3600 seconds in one hour. Amperage is defined as 1 Coulomb per second and is directly
proportional to ampere-hours.
2.7 10 
3600=750 
b) The charge of a single electron is -1.602·10-19 C. The negative sign indicates that the particle delivered will
be an electron. Simple division gives the solution:
2.7 101.602 10
1 
= 1.685 10 

G. Rizzoni, Principles and Applications of Electrical Engineering, 6th Edition Problem solutions, Chapter 2
2.4
PROPRIETARY MATERIAL. © The McGraw-Hill Companies, Inc. Limited distribution permitted only to teachers and
educators for course preparation. If you are a student using this Manual, you are using it without permission.
Problem 2.4
A three rate charge cycle is used to charge a battery. The current to the battery is held at 30 mA for 6 h and then
switched to 20 mA for the next 3 h.
Solution:
Known quantities:
See Figure P2.4
Find:
a) The total charge transferred to the battery.
b) The energy transferred to the battery.
Analysis:
a) Current is equal to 
 , therefore given the current and a duration of that current, the transferred
charge can be calculated by the following equation:
=
The two durations should be calculated independently and then added together.
0.03021600=648
0.02010800=216
648+216=
b) P=V·I, therefore, an equation for power can be found by multiplying the two graphs together.
First separate the voltage graph into three equations:
0 h → 3 h := 9.26 · 10+ 0.5
3 h → 6 h := 5.55 10
6 h → 9 h := 1.11 101.9
Next, multiply the first two equations by 0.03A and the third by 0.02A.
0 h → 3 h := 2.77 10+ 0.015
3 h → 6 h := 1.66 10
6 h → 9 h := 2.22 100.038
Finally, since Energy is equal to the integral of power, take the integral of each of the equations for their
specified times and add them together.
0 h → 3 h :=.
+ 0.015|10800
0= 178.2 J
3 h → 6 h :=.
|21600
10800= 290.43 J
6 h → 9 h :=.
+ 0.038|32400
21600 = 1057.8 J
 = 
Problem 2.5
Batteries (e.g., lead-acid batteries) store chemical energy and convert it to electric energy on demand. Batteries do
not store electric charge or charge carriers. Charge carriers (electrons) enter one terminal of the battery, acquire
electrical potential energy, and exit from the other terminal at a lower voltage. Remember the electron has a negative

G. Rizzoni, Principles and Applications of Electrical Engineering, 6th Edition Problem solutions, Chapter 2
2.5
PROPRIETARY MATERIAL. © The McGraw-Hill Companies, Inc. Limited distribution permitted only to teachers and
educators for course preparation. If you are a student using this Manual, you are using it without permission.
charge! It is convenient to think of positive carriers flowing in the opposite direction, that is, conventional current,
and exiting at a higher voltage. All currents in this course, unless otherwise stated, are conventional current.
(Benjamin Franklin caused this mess!) For a battery with a rated voltage = 12 V and a rated capacity = 350 A-h,
determine
a. The rated chemical energy stored in the battery.
b. The total charge that can be supplied at the rated
Solution:
Known quantities:
Rated voltage of the battery; rated capacity of the battery.
Find:
a) The rated chemical energy stored in the battery
b) The total charge that can be supplied at the rated voltage.
Analysis:
a)
∆V≡∆PE
c
∆QI=∆Q
∆t
Chemical energy = ∆PEc= ∆V⋅ ∆Q= ∆V⋅I⋅ ∆t
( )
=12 V350 A−hr 3600 s
hr =15.12 MJ.
As the battery discharges, the voltage will decrease below the rated voltage. The remaining chemical energy stored
in the battery is less useful or not useful.
b)
∆Q
is the total charge passing through the battery and gaining 12 J/C of electrical energy.
.MC26.1
hr
s
3600hr
s
C
350hrA 350 =⋅==∆⋅=∆ tIQ
Problem 2.6
What determines the following?
a. How much current is supplied (at a constant voltage) by an ideal voltage source.
b. How much voltage is supplied (at a constant current) by an ideal current source.
Solution:
Known quantities:
Resistance of external circuit.
Find:
a) Current supplied by an ideal voltage source
b) Voltage supplied by an ideal current source.
Assumptions:
Ideal voltage and current sources.
Analysis:
a) An ideal voltage source produces a constant voltage at or below its rated current. Current is determined by the
power required by the external circuit (modeled as R).
IVP
R
V
I
s
s
⋅==