sunumaths-document-1

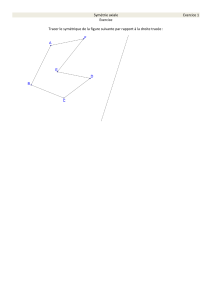
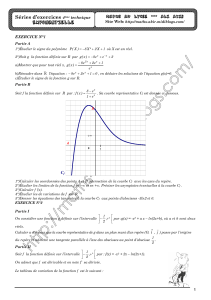
------------------------------------ 1 -----------------------------------------
Extrait de XY-MATHS caps vers la réussite  M. THIAO Professeur au lycée de Bambey
77 360 32 35 / 76299 00 99
LE MOT DE L’AUTEUR
XY–MATHS CAP VERS REUSSITE cap vers UNE COLLECTION
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Nous avons repris dans ce manuel XY- MATHS cap vers la
réussite  les principes qui avaient guidé la rédaction du
manuel de seconde : XY- MATHS cap vers la réussite.
Nous avons construit chacun des chapitres selon une structure
simple.
 Un cours clair et détaillé où l’essentiel est donné (définition,
remarques, théorèmes, propriétés)
 A la fin de chaque sous-titre du cours ; des exercices
d’applications résolus pour appliquer le cours.
 Une série d’exercices est proposée pour chaque cours pour
mettre en application les méthodes étudiées.
Nous remercions les éditions harmattan Sénégal pour leurs
confiances renouvelées dans nos choix et leurs expertises
apportées à la réalisation de l’ensemble de notre projet
Nous espérons que ce manuel sera bien accueilli et qu’il rendra
à ses utilisateurs, apprenants et enseignants, les services qu’ils
peuvent en attendre. Nous accueillerons avec intérêt toutes les
remarques et observations qu’ils voudront bien nous adresser au
77 360 32 35 (WhatsApp)

------------------------------------ 2 -----------------------------------------
Extrait de XY-MATHS caps vers la réussite  M. THIAO Professeur au lycée de Bambey
77 360 32 35 / 76299 00 99
GÉNÉRALITÉS SUR LES FONCTIONS
NUMÉRIQUES D'UNE.
. VARIABLE RÉELLE
 Ce que dit le programme…..
Contenus
Commentaires
Compétences exigibles
Il est essentiel d'accorder une place importante aux représentations graphiques et aux
résolutions graphiques de certains problèmes. Dans cette partie, aucune théorie ne sera
faite : on traitera seulement des exemples simples.
1) Fonctions associées à
une fonction
;
 ;
Application à la
représentation
graphique des fonctions
polynômes du second
degré et de quelques
fonctions
homographiques.
2) Eléments de symétrie
de la courbe représentative
d'une fonction
3) Représentation
graphique de la réciproque
d'une
bijection
 Il s'agit d'utiliser des
transformations pour
construire les
représentations
graphiques des
fonctions associées à
f à partir de la
représentation de f.
 Toute recherche
systématique est
exclue.
 On pourra utiliser
un changement de
repère ou les
formules usuelles (à
établir) :
et 
ou 
 Déterminer graphiquement
l'image ou l'image réciproque
d'un intervalle.
 Construire, à partir de la
représentation graphique d'une
fonction, celles des fonctions
qui lui sont associées.
 Démontrer qu'un point est
centre de symétrie de la
représentation graphique d'une
fonction.
 Démontrer qu'une droite
est axe de symétrie de la
représentation graphique d'une
fonction.
 Construire la
représentation graphique de la
réciproque d'une fonction
bijective.

------------------------------------ 3 -----------------------------------------
Extrait de XY-MATHS caps vers la réussite  M. THIAO Professeur au lycée de Bambey
77 360 32 35 / 76299 00 99
PLAN DU CHAPITRE_________________________
I. DEFINITION
1.1 FONCTION
1.2 FONCTION NUMERIQUE
II. RAPPELS SUR LES FONCTIONS
2.1 ENSEMBLE OU DOMAINE DE DEFINITION OU
D’EXISTENCE
2.2 COURBE D’UNE FONCTION
2.3 SENS DE VARIATION D’UNE FONCTION
2.4 EXTREMUMS D’UNE FONCTION
2.5 FONCTION MINOREE, MAJOREE OU BORNEE
2.6 COMPARAISONS DE FONCTIONS
2.7 COMPOSITION DE DEUX FONCTIONS
III. ELEMENTS DE SYMETRIES D’UNE COURBE
3.1 RAPPELS
3.2 AXE DE SYMETRIE
3.3 CENTRE DE SYMETRIE D’UNE COURBE
IV. FONCTIONS ASSOCIEES A UNE FONCTION
4.1 RÉFLEXIONS
4.2 TRANSLATIONS
4.3 AFFINITÉS ORTHOGONALES
V. REPRESENTATION GRAPHIQUE DE LA
RECIPROQUE D'UNE BIJECTION
5.1 PROPRIETES FONDAMENTALES

------------------------------------ 4 -----------------------------------------
Extrait de XY-MATHS caps vers la réussite  M. THIAO Professeur au lycée de Bambey
77 360 32 35 / 76299 00 99
APERÇU HISTORIQUE
Le terme de fonction a été introduit par le mathématicien allemand LEIBNIZ Gottfried
Wilhelm (1646-1716) en 1673 dans un manuscrit inédit "La Méthode inverse des
tangentes ou à propos des fonctions". "J'appelle fonctions toutes les portions des
lignes droites qu'on fait en menant des droites indéfinies qui répondent au point fixe
et aux points de la courbe; comme sont les abscisse, ordonnée, corde, tangente,
perpendiculaire, sous-tangente ...et une infinité d'autres d'une construction plus
composée, qu'on ne peut figurer. "LEIBNIZ Gottfried Wilhelm (1646-1716), in La
Méthode inverse des tangentes ou à propos des fonctions, 1673. Cette définition se
retrouve dans des articles de 1692 et 1694 et est reprise par le mathématicien
suisse BERNOULLI Johann francisé Jean (1667-1748) en 1697. BERNOULLI
Jean (1667-1748) en 1718 propose la définition suivante :
"On appelle fonction d'une grandeur variable une quantité composée, de quelque manière
que ce soit, de cette grandeur variable et de constante."
Il propose la notation : Φx
VI. DEFINITION
6.1 FONCTION
Soit  et  deux ensembles non vide, on appelle fonction de  vers  
toute procédé qui pour  élement de  ( ensemble de départ) onassoci au plus
(maximun) un élement  de  ( ensemble d’arrivé).
On note :  : 
On dit que  est une fonction de  vers 
  est l’antécédent de  par la fonction.
  est l’image de  par la fonction.
NB : pour une fonction  ; un antécédent  ne peut pas avoir plus qu’une image
cependant une image  peut avoir plus qu’un antécédent

------------------------------------ 5 -----------------------------------------
Extrait de XY-MATHS caps vers la réussite  M. THIAO Professeur au lycée de Bambey
77 360 32 35 / 76299 00 99
6.2 FONCTION NUMERIQUE
On appelle fonction numérique toute fonction dont l’ensemble d’arrivé est  ou une
partie de  . Si l’ensemble de départ est  ou une partie de, on dit que la fonction
est une fonction numérique d’une variable réelle.
Exemples
 ,  et  sont des fonctions numériques d’une variable réelle.
VII. RAPPELS SUR LES FONCTIONS
7.1 ENSEMBLE OU DOMAINE DE DEFINITION OU
D’EXISTENCE
7.1.1 Définition
Soit 
 Une fonction ; on appelle ensemble ou domaine de définition
ou d’existence noté  l’ensemble des réelles  de l’ensemble de départ  et qui
ont des images  dans l’ensemble d’arrivé  par la fonction .
7.1.2 Propriétés
 Toute fonction polynôme est définie dans son ensemble de départ
 Toute fonction rationnelle  telque 
 est définie pour tout  appartenant à
son ensemble de départ tel que 
 Toute fonction irrationnelle  telque  est définie pour tout 
appartenant à son ensemble de départ tel que 
ATTENTION : Une fonction peut aussi être plus compliquée, à savoir (par exemple) un
quotient sous une racine ou une racine au dénominateur d’un quotient.
NB : Pour une fonction numérique d’une variable réelle donnée si son ensemble de
départ n’est pas précisé alors on considère que c’est 
EXERCICE D’APPLICATION :
Pour chacune des fonctions suivantes, déterminer son ensemble de définition
 ; 
 ;  
 ;  ; 
 ; 
 ;  