E.C.miroir1

1AMPLIFICATEUR CHARGE PAR MIROIR DE COURANT
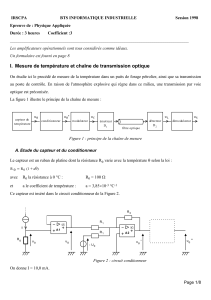
1. On donne le schéma de principe en figure 1, dans lequel le transistor est centré. En
négligeant dans cette première question, l’effet de la résistance interne du transistor rce,
calculer le gain en tension
Av
v
s
e
=
en fonction de VCC1 et de UT.
+ VCC1
R
vsve
T1
Figure 1
2. Dans les circuits intégrés, on cherche, pour plusieurs raisons, à avoir un gain en tension par
étage de quelques milliers. Calculer, d’après la question précédente, la valeur de VCC1
nécessaire pour obtenir une amplification de 2000, le montage travaillant à la température
ambiante de 25°C.
3. Dans le but de diminuer cette tension jugée excessive, on va remplacer la résistance R par
une charge dynamique (ou charge active), constituée par le transistor de sortie d’un miroir
de courant (figure 2).
Calculer le rapport
I
I
ref
0
en fonction des paramètres des transistors. Les deux transistors sont
au silicium et identiques.
T2T3
R1
C3
Ire
f
Io
VBE
Figure 2
1 © Ph. ROUX 2005 http://rouxphi3.perso.cegetel.net

4. Montrer que Iref est à peu près égal à
V
R
CC 2
1
. Calculer alors la sensibilité S du courant Io aux
variations de VCC2, c’est à dire le rapport du pourcentage de variation de Io au pourcentage de
variation de VCC2 qui l’a provoquée, soit :
S
I
I
V
V
I
V
V
I
o
o
CC
CC
o
CC
CC
o
==
∆
∆
∆
∆
2
2
2
2
5. Dessiner le schéma équivalent du miroir aux petites variations, et déterminer en utilisant la
méthode de l’ohmmètre, la résistance interne ro équivalente au dipôle vu entre le collecteur
de T3 et la masse. Faire l’application numérique avec : tension de Early VA = 50 V, Iref = 0,6
mA et β = 100.
6. On branche maintenant le miroir en charge de T1 (figure 3). T1 est parfaitement
complémentaire de T2 et T3. Donner le schéma équivalent global aux petites variations, en
remplaçant le miroir (partie encadrée) par le dipôle équivalent déterminé à la 5ème question.
+ VCC2
T2T3
R1
Ire
f
Io
ve
vs
Figure 3
7. Déterminer littéralement le nouveau gain
Av
v
s
e
=
.
8. L’écrire en fonction de VA et UT, et faire l’application numérique.
9. La sensibilité S étant jugée excessive, et le gain étant limité par la valeur trop faible de la
résistance de sortie ro, on imagine un miroir amélioré, conforme au schéma de la figure 4, où
les transistors T2 et T3 sont les mêmes que les précédents.
+ VCC2
T2
T3
R1C3
Ire
f
Io
R2 VBE2
Ire
f
Io
Figure 4

En négligeant les courants de base, écrire l’expression de Iref en fonction de VBE2.
En déduire l’expression de Io en fonction de Iref, Ut, R2 et ISBC (le courant de saturation de la
jonction de collecteur).
10. On donne R2 = 1 kΩ, UT = 25 mV et ISBC = 10-14 A. Tracer le graphe du courant Io en
fonction de Iref pour Iref compris entre 0 et 2 mA.
11. On donne VCC2 = 15 V. Calculer la nouvelle valeur de R1 nécessaire pour avoir Io = 0,6 mA.
Donner la valeur de R1 normalisée à 10% la plus proche.
12. A partir de l’expression de la 9ème question, calculer la valeur de la sensibilité S pour ce
nouveau miroir. Faire l’A.N.
13. Donner le schéma équivalent complet de ce miroir, aux petites variations.
14. On va chercher la résistance ro du dipôle équivalent à ce nouveau miroir. R1 et rce2 ayant une
valeur assez grande pour être négligées, écrire les deux équations aux nœuds régissant le
montage.
15. Calculer la nouvelle valeur de ro.
16. En donner une expression approchée, compte tenu des valeurs numériques habituelles des
paramètres : β = 100. Faire l’A .N.
17. Trouver alors la nouvelle expression du gain de l’amplificateur. Faire l’A.N.

CORRECTION
1. Schéma aux variations du montage :
gm.vbe Rrbe
ve
vbe
vs
v
vgR
s
e
m
=−
avec la transconductance :
gI
U
m
C
T
=
.
Si le transistor est centré sur sa droite de charge, alors :
IV
R
C
CC
=
1
2
v
v
V
U
s
e
CC
T
=− 1
2
On rappelle que : UT = 25 mV à 25°C.
2. Pour un gain de 2000, il faut choisir VCC1 = 100 V !
3. Les transistors ont la même tension VBE et obéissent à la loi :
II V
U
C SBC
BE
T
=exp( )
. Les
transistors intégrés sont aussi identiques et possèdent donc le même courant ISBC.
Ce miroir de courant à transistors PNP est classique, aussi on trouvera facilement :
II
o ref
=
+
1
12
β
Si le gain en courant β est suffisamment grand alors :
II
oref
≈
4.
IVV
R
V
R
ref
CC BE CC
=−≈
2
1
2
1
dans la mesure où : VBE << VCC2.
Le miroir de courant est tel que :
IV
R
o
CC
≈
2
1
ddI
dV
R
Iref o
CC
== 2
1
On en déduit : S = 1. La sensibilité de Io aux variations de VCC2 est importante.
5. Schéma équivalent du miroir aux petites variations.

Req
gm2.vbe
2
gm2.vbe3
rce3 u
+
-
i
vbe
2
vbe3
Req = rbe2//rbe3//rce2//R1
B2 B3 C2 C
3
E2 E3
Selon la méthode de l’ohmmètre, la résistance ro est égale au rapport de u/i.
vv Rgv
bebe eq m be
2322
==−
. Cette équation a pour solution : vv
bebe
230==
Dans ces conditions : ro = rce3.
rV
Ik
o
A
o
≈=83 Ω
6. Nouveau schéma équivalent :
rbe1
gm1.v
e
rce1v
e
E2 E3
rovs
7.
Av
vgr r
s
e
mce o
==−
11
(//)
8. Gain en tension :
AI
U
V
I
V
U
o
T
A
o
A
T
=− =− =−()
221000
Ce gain en tension est proportionnel à la tension de Early des transistors.
9. Pour le transistor T2 :
II V
U
ref SBC
BE
T
=exp( )
2
avec :
VRI
BE o22
=−
.
On en déduit :
IU
R
I
I
o
Tref
SBC
=
2
ln( )