resolution-par-methode-norton-millman-kennely-14

LECON 4 : RESOLUTION PAR LA METHODE DE NORTON, MILLMAN ET KENNELY
CHAPITRE 1 : ELECTROCINETIQUE 19
RESOLUTION PAR LA METHODE DE NORTON,
MILLMAN ET KENNELY
1 - METHODE DE NORTON
1.1 - Introduction
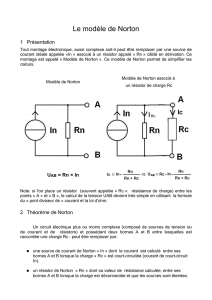
Le théorème de Norton va nous permettre de réduire un circuit complexe en générateur de courant réel.
Ce générateur possède une source de courant (IN) en parallèle avec une résistance (RN),
N
N
NI.
R RR
I + =
1.2 - Principe
Le courant de Norton IN est obtenu par calcul ou par une mesure après avoir court-circuité les bornes A
et B,
La résistance interne RN s'obtient de la même façon que celle du théorème de Thevenin (RN = RTh),
1.3 – Applications
1.3.1 - Exercice 1
On considère le circuit électrique donné par la figure suivante :
 On donne : E = 8 V ; R1 = 4 Ω ; R2 = 12 Ω ; R3 = 9 Ω
 Calculer le courant I qui traverse la résistance R3 en
appliquant le théorème de Norton,
=
R
I
B
A
Circuit
électrique IN R
I
B
A
RN
R1 R3
E
R2
I
A
B
Solution :
1) Calcul de IN
On débranche la résistance R3 et on court-circuite les bornes A et B, la configuration sera donc :
A 2
4
8
R
E
I 1
N===
A
B
R1
E
R2 =
A
B
R1
E
IN IN

LECON 4 : RESOLUTION PAR LA METHODE DE NORTON, MILLMAN ET KENNELY
CHAPITRE 1 : ELECTROCINETIQUE 20
2) Calcul de RN
R3 étant toujours débranchée, on court-circuite E, la configuration sera donc :
Ω=
+
×
=
+
= 3
124 124 R R .RR
R 21
21
Th
R2
A
B
R1
3) Calcul de I
A 0,5 2
933
I
R R R
I N
3N
N=
+
=
+
=
1.3.2 - Exercice 2
On considère le circuit électrique donné par la figure suivante :
IN R3
I
B
A
RN
 On donne : E1 = 10 v ; E2 = 5 v ; R1 = R3 = R4 = 100 Ω ; R2 =
50 Ω
 Calculer le courant I en appliquant le théorème de Norton,
Solution :
1) Calcul de IN
On débranche la résistance R4 et on court-circuite les bornes A et B, la configuration sera donc :
R1
E1
R2
A
B
R4
I
R3
E2
A 0,15
100
5
100
10
I I I
R
E
R
E
21N
3
2
2
1
1
1=+=+=⇒
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
=
I
I
R1
E1
R2
A
B
R3
E2
IN =R1
E1
R3
E2
IN
I1 I2
A
B

LECON 4 : RESOLUTION PAR LA METHODE DE NORTON, MILLMAN ET KENNELY
CHAPITRE 1 : ELECTROCINETIQUE 21
2) Calcul de RTh
Ω=
++
= 52
R
1
R
1
R
11
R
321
Th
R2
A
B
R1 R3
3) calcul de I3
A 0,03 I
R R R
I N
4N
N=
+
=
IN
1.3.3 - Exercice 3
On considère le circuit électrique donné par la figure suivante :
 On donne : E1 = 10 v ; E2 = 2 v ; R1 = 60 Ω ; R3 = 120 Ω ; R4 =
180 Ω ; R2 = 240 Ω ; R5 = 90 Ω
 Calculer le courant I en appliquant le théorème de Norton,
Solution :
1) Calcul de IN
A 0,04
R R R
R R R
R
E
I
R R R
R R R
R : avec
R
E
I : a On
R R R
R R R
I I
I
R R R
I
I
R R R
I
I - I I
54
5
31
3
eq
N
54
5
31
3
eq
eq
54
5
31
3
N
54
5
4
31
3
1
41N
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
=⇒
+
+
+
==
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
=⇒
+
=
+
=
=
R4
I
B
A
RN
R4
R3
R5
E1
R1
R2E2
A
D
C
B I2
IN R4
B
A
I
RN
=
R4
R3
R5
E1
R1
IN
A
D
C
B E1 BD
A
C
R4
R3
R5
R1 IN
I1 I3
I5
I4
I

LECON 4 : RESOLUTION PAR LA METHODE DE NORTON, MILLMAN ET KENNELY
CHAPITRE 1 : ELECTROCINETIQUE 22
2) Calcul de RTh
Ω=
+
+
+
= 96,42
RR .RR
RR .RR
R 53
53
41
41
Th
3) calcul de I2
(
)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
+
+
=
=+
mA 17,4
R R E I R
I
0 IR - I - I R E
2N
2NN
2
222NN2
2 - THEOREME DE MILLMANN
2.1 - Introduction
Ce théorème très pratique permet de déterminer la différence de potentiel aux bornes de plusieurs
branches en parallèle (UAB),
2.2 - Principe
⎪
⎩
⎪
⎨
⎧
==
Σ
Σ
Σ
Σ
=
=
=
=
branhe la de admittance :Y
branche la de numéro : i
: Avec
Y
.Y E
Ri
1
Ri
Ei
U
i
n
1i
ii
n
1i
n
1i
n
1i
AB
Remarque :
Si dans une branche, il n'y a pas de générateur, on considère que la f.e.m correspondante est nulle,
2.3 – Applications
2.3.1 - Exercice 1
On considère le circuit électrique donné par la figure suivante :
=
R4
R3
R5
R1
A
D
C
B
A
C
B
C
R4
R3
R5
R1
D
IN R2
I2
B
A
RN
IN - I2
E2
R1
E1
A
B
R2
E2
Rn
En
UAB

LECON 4 : RESOLUTION PAR LA METHODE DE NORTON, MILLMAN ET KENNELY
CHAP 23
ITRE 1 : ELECTROCINETIQUE
 On donne : E1 = 5 v ; E2 = 20 v ; R1 = 5 Ω ; R2 = R3 =
10 Ω
 Calculer UAB,
R1
E1
R2
A
B
R3
E2
UAB
Solution :
Calcul de UAB : V 7,5
10
1
10
1
5
1
0
10
20
5
5
R
1
R
1
R
1R
0
R
E
R
E
U
321
32
2
1
1
AB =
++
++
=
++
++
=
2.3.2 - Exercice 2
On considère le circuit électrique donné par la figure suivante :
 On donne : E1 = 5 v ; E2 = 20 v ; E3 = 4 V ; R1 = R3 = 2 Ω ;
R3 = 1 Ω
 Calculer UAB,
Solution :
1) Calcul de UAB
V 0,75
2
1
1
1
2
12
4
1
5
2
R
1
R
1
R
1R
E
R
E
R
E
U
321
3
3
2
2
1
1
AB =
++
−+−
=
++
−+−
=
2) Calcul de I dans R4
 Calcul de ETh : on remarque que ETh = UAB = 0,75 V
 Calcul de RTh
Ω=
++
= ,50
R
1
R
1
R
11
R
321
Th
R1
E1
R2
A
B
E2
UAB
R3
E3
R2
A
B
R1 R3
3) calcul de I RTh
A 0,3
R R E
I 4Th
Th =
+
=
R
A
B
I
ETh 4