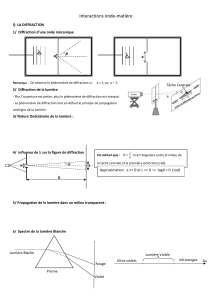
1 Points essentiels: Nature ondulatoire de la lumière. 2 1) Le phénomène de diffraction. 2) Diffraction de la lumière par une fente. Diffraction de la lumière par une fente. Les caractéristiques. Diffraction de Fresnel . Principe de Huygens Diffraction de Fraunhofer. Interférence et diffraction combinées. Étude qualitative. a. Nature ondulatoire de la lumière. 1) Le phénomène de diffraction: 3 Ce phénomène apparaît lorsqu’un faisceau de lumière éclaire un écran opaque percé d’une petite ouverture. Là encore les dimensions sont relatives à la longueur d’onde de la lumière incidente. La tache lumineuse observée sur un écran placé en arrière de l’écran percé montre un étalement angulaire du faisceau transmis. Par exemple, si un faisceau incident tombe sur une fente, l ’ouverture angulaire du faisceau émergent augmente lorsque la largeur de la fente diminue. Ouverture carrée Ouverture circulaire a . Nature ondulatoire de la lumiere 2) Le phénomène de diffraction: Ecart angulaire θ : θ= λ a λ : longueur d’onde (m) a : dimension caractéristique de l’obstacle Phénomène significatif si a ≈ λ ou a < λ (lumiere : a ≈ 10-7 m) 4 B. Diffraction de la lumière par une fente : θ faible : tan θ ≈ θ Largeur de la tache centrale : d=2 λD a Utilisation : mesure de λ ou taille de petits objets (cheveu…) 5 c. Les caractéristiques : *Figure de diffraction* La nature ondulatoire de la lumière révélée par une simple lame de rasoir. 6 En 1819, l'Académie des sciences de Paris mettait au concours la question de la diffraction de la lumière. Augustin Fresnel, un jeune provincial, proposa dans son mémoire une solution qui nous est aujourd'hui familière, fondée sur l'hypothèse d'une lumière constituée d'ondes qui interfèrent entre elles. 7 « Si la source ou l’écran se trouve près de l’ouverture ou de l’obstacle, les fronts d’onde sont sphériques et la figure est assez complexe .C’est ce que l’on appelle la diffraction de Fresnel. Une partie de la lumière pénètre dans la région d’ombre géométrique et l’on observe des franges près des bords de l’obstacle » 8 e. Principe de Huygens: Tout élément de la surface dS centré en M de la surface d’onde (t) peut-être considéré comme une source élémentaire, secondaire, d’ondes sphériques dont l’amplitude complexe en un point P est proportionnel à : e jk r K A incidentdS r Où K() est un facteur d ’inclinaison L’amplitude en un point P est proportionnelle à la somme des amplitudes de toutes les ondes émises par les sources fictives réparties sur la surface (t) . Dans la suite nous nous placerons dans le cas particulier où est petit K() = 1. Diffraction de Fraunhofer 9 f. Diffraction de Fraunhofer Tentons d'écrire la répartition d’intensité ou d’amplitude créer par un objet diffractant quelconque (ouverture rectangulaire ou circulaire, …) et observée sur écran placé a une grande distance de l ’objet. Nous utiliserons ici l’approximation de Fraunhofer qui suppose que les rayons lumineux incidents sont faiblement inclinés par rapport à l ’axe. 10 L’objet diffractant est caractérisé par sa transparence en amplitude définie comme le rapport de l’amplitude complexe émergent par l’amplitude complexe incidente : Aémergent x, y Aincident Objet totalement opaque : x, y 0 Objet totalement transparent : x, y 1 L’amplitude incidente est de la forme : Ai M e L’amplitude émergente peut s ’écrire : D’après le principe de Huygens : jk AM x, y e dAM , P x, y .e Avec : r MP D 2 x y 2 11 x2 y 2 2D 2 jk jk x2 y 2 2D x2 y 2 2D e jkr . .dS r Finalement l’amplitude complexe du champ électrique en P : AP dAM , P x, y .e jk x2 y 2 2D e jkr . .dx.dy r La distance d’observation étant grande on peut écrire : rD 2 2 x y 1 D2 D2 x 2 y 2 D1 2 2 2D 2D 2 2 x y r D 2D 2D L’amplitude en P devient : A P x, y .e jk x2 y 2 2D . e x 2 y 2 jk D 2D 2 D 2 2 x y D 2D 12 e jk D D e jk D D x, y .e x, y .e x2 y 2 jk 2D jk x2 y 2 2D .e .e 2D x 2 y 2 jk 2 D 2 D jk x2 y 2 2D .dx.dy .e jk .dx.dy 2 2 2D .e jk x y D .dx.dy On obtient après simplification : AP A , e jk 2 2 2D jk e jkD x , y . e D Constante x y D .dx.dy On négligera ce terme car il va s’annuler lorsqu’on cherchera l’expression de l’intensité obtenue en multipliant par le conjugué complexe de A. A , x, y .e j 2 x y D D .dx.dy On reconnaît dans cette dernière écriture l’expression de la transformée de Fourier de la transparence (x,y). A , , D D ou avec tg tg L ’intensité s ’écrira : I , A , A , 13 A , , D D , , , D D D D D D 2 f.1. Exemples f.1.1. Fente infiniment longue La fonction transparente peut-être décrite par la fonction rectangle de largeur e : x x rect e L’amplitude en un point P de l’écran est proportionnelle à la transformée de Fourier de : A( P) A( ) e.sin c e D Donc pour l’intensité, on a : I( ) I 0 .sin c 2 e D Avec I0 l’éclairement maximal pour =0 14 f.1.2. Fente rectangulaire La fonction transparente peut-être décrite par la fonction rectangle à deux dimensions : x y y y x, y rect , rect rect a b b b L’amplitude en un point P : A( , ) ab.sin c a .sin c b D D Donc pour l’intensité, on a : I( , ) I 0 .sin c 2 a .sin c 2 b D D Avec I0 l’éclairement maximal pour =0 et =0 15 *Répartition en intensité de la diffraction d’une fente rectangulaire. 16 f.2. Ouverture circulaire La fonction transparente peut-être décrite par la fonction : x, y Circ , x y R R Fonction de Bessel de première espèce L’amplitude en un point P : J Z A ( , ) 2 1 Z 2 2 Z 2R D avec Donc pour l’intensité, on a : J Z I( ) 1 Z 17 2 Cette tache de diffraction est plus connue sous le nom de “Tache d’Airy”. On peut en première approximation donner la valeur du rayon de l’anneau central : 1.22 18 2R Avec R rayon du trou * Deux fentes infiniment longues: y x a L 2,a L 2 1 si x x a L 2, a L 2 0 ailleurs xmin A(u ) e j 2ux xmax xmax dx e xmin j 2ux dx avec xmax a L 2 xmin a L 2 1 j 2uxmin j 2uxmax j 2uxmax j 2uxmin e e e e j 2u 1 sin 2uxmin sin 2uxmax u u 2 avec D sin uL cos2ua u A (u ) 19 Finalement : I(u ) sin c 2 uL cos2 2ua Diffraction 20 Interférences f.3.Théorème de Babinet Les figures de diffraction produites par deux écrans complémentaires sont identiques, sauf au voisinage immédiat de l’image géométrique. Prenons l’exemple d’une fente, on sait que la figure de diffraction est : a a 1 si x , x 2 2 0 ailleurs I(u) I 0 .sin c 2 ua L’écran complémentaire : a a 0 si x , c x 2 2 1 ailleurs a 2 A c (u ) e j 2ux dx e j 2ux a 2 a 2 dx e j 2ux L avec L a 1 jua e e j 2uL e j 2uL e jua j 2u A c (u ) sin c2uL sin cua A c (u ) 21 L dx e j 2uxdx a 2 Ic (u ) Ac (u ) sin c2uL sin cua 2 2 Ic (u ) sin c 2 ua 2 sin cua sin c2uL sin c 2 2uL 1.5 Ic I 1 1.2 1 0.8 0.6 0.5 0.4 0.2 0 0 L=100*a L=1000*a Les figures de diffraction sont uniquement différentes dans la zone proche de l’axe. 22 Répartition en amplitude Répartition en intensité 23 g. Interférence et diffraction combinées: Dans la description de l’expérience de Young, nous n’avons pas tenu compte de la figure de diffraction produite par chaque fente. Si l’écran est très éloigné, les fentes produisent des figures de diffraction qui se superposent. On observe la figure de diffraction d’une fente simple avec des maxima d’intensité plus élevée. On dit que la figure d’interférence a pour enveloppe la figure de diffraction produite par une fente simple. 24 Lors de l’étude de l’interférence à 2 fentes (ou plus), nous avons supposé qu’il s’agissait de fentes étroites. Ainsi l’intensité due à une fente était la même Io pour tous les points P sur l’écran, peu importe l’angle d’observation . Si la fente n’est pas étroite, mais possède une largeur a, l’intensité sur l’écran n’est pas indépendante de l’angle mais décroît à mesure que l’angle augmente. Spectre continu 25 25 *Interférence* I n t e n s i t é 1. La majeure partie de la lumière est concentrée dans le maximum central lorsque sin varie de –/a à + /a . 2. Le premier minimum apparaît lorsque sin = /a . 3. La largeur du maximum central décroît si a augmente. 26 26
