Fascicule electrocinetique

51
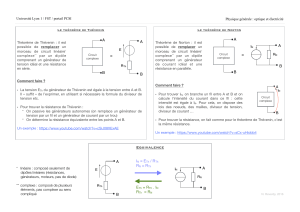
Exercice 1: Calculer la résistance de Thévenin dans chacune des branches du réseau suivant .
Solution : L’étudiant complètera sur les figures les valeurs des résistances et indiquera la technique
de transformation
Rth =
Rth =
F
i
g
u
r
e
1

52
Rth =
Rth =
Rth =
Rth =

53
Exercice 2 : Calculer le courant dans les différentes branches du
réseau ci-contre . :
A.N : R1 = 2 Ω ; R2 = 9 Ω ; R3 = 7 Ω ; R4 = 6 Ω ; R5 = 3 Ω ;
E2 = 18 V ; E5 = 3V
Solution : Calculons les courants dans le réseau électrique suivant par la méthode de Maxwell
- Choisissons des courants de mailles et fixons les mêmes sens de parcours
-
1
I
;
3
I
;
5
I
-Ecrivons les matrices des résistances, des courants et des F.e.m.
5
2
2
5
3
1
544
44322
221
E
E
E
I
I
I
RRR0
RRRRR
0RRR
Calculons les déterminants des résistances, des courants
1
I
;
3
I
;
5
I
, et écrivons les solutions :
A 1.231
R
I
I1
1
;
A 0.496
R
I
I3
3
;
A 0.664 R
I
I5
5
;
534
312 I-II III
( attention au signe )
Solution : Calculons les courants dans le réseau électrique par la méthode de Thévenin; L’étudiant
complètera le tableau.

54
(suite du calcul page suivante 1)
(suite du calcul page suivante 2)
(suite du calcul page suivante 3)
(suite du calcul page suivante 4)
(suite du calcul page suivante 5)
23
54
54
23
54
54
th RR
RR RR
RR
RR RR
R
[(R4//R5)+R3]//R1
R =
[(R4//R5)+R3]//R2
(R1//R2)+(R4//R5)
R =
[(R1//R2)+R3]//R5
R =
[(R1//R2)+R3]//R4
R =
?ix
Par Maxwell
3 chemins possibles
3 voies possibles
'
x1
2BA
)i(R
E)1(VV
"
24
5BA
iR
EVV
)i(RE)1(oxRV x221AB 
?ix
Par Maxwell
4 chemins possibles
)i(R)i(R
E)1(VV
y4
'
x2
2BA
ix et iy par la loi à la maille
''iREVV 55BA 
i’’ par Maxwell
i’’2 par Maxwell
Vth =
ith =
coupée brancheth
th
RR V

55
1)
)i(RE)1(oxRV x221AB 
- Kirchoff
- Maxwell
544
4432
R R- R
RRRR
5
2
E
E
I
I
z
x
- Thévenin
- Superposition
(
y
I
Courant de branche commune ;
zx II ;
même sens courant de maille)
ix
R
R
Iix
x
1
RR
V
I
th
AB
x
2)
 BA VV
3 voies possibles
choix sur la maille
),,( 221 ERR
'
x12BA )i(RE)1(VV 
Maxwell
x
I
et
z
I
courants fictifs de Maxwell
544
4431
R R- R
RRRR
5
0
E
I
I
z
x
R-
54
R
E
R
Iix
x
R
5
41
2E
R
RR
EVV BA 
2
RR
V
I
th
th
th 
Rechercher
x
I
par Thévenin ?
3)
"
245 IREVV BA 
?
'
2
I
4322
221
R R- RR
RRR
2
2
"
2
'
2E
E
I
I
4) et 5) à compléter par l’étudiant.
:?ix