Cours ENSEMBLES de NOMBRES
I - ENSEMBLE DE NOMBRES
« Dieu fit le nombre entier, le reste est l’oeuvre de l’homme » - KRONECKER (mathématicien allemand 1823-1891)
NOMBRES DEFINITION - HISTOIRE Ensemble
Notation Exemples
Entiers
naturels Ce sont les nombres entiers et positifs.
Le besoin de compter.
introduit cinq siècles avant notre ère par les Babyloniens,
Egyptiens, Grecs, Indiens .
Le chiffre zéro, n’a été introduit que vers la fin du Ier millénaire, par
les Indiens. Il s’est imposé progressivement dans tous les systèmes de
numération, et est devenu le plus petit des entiers naturels.
# N vient de l’italien : « Naturale ».
N
0 , 1 , 2 , 3
. . .
1 000
Entiers
relatifs Ce sont tous les nombres entiers (positifs ou négatifs ).
De IN à Z : solution de l’équation a + x = b.
introduit en Europe au cours du moyen âge.
# Z vient de l’allemand : « Zahl » ( nombre ).
Z
. . . ,
-3 ,-2 , -1 ,
0 , 1 , 2 ...
- 72 050
Décimaux Ce sont les nombres qui peuvent s’écrire sous la forme p
m
10 ,
avec m entier relatif, et p entier naturel.
Ex : 3
4
0,0004 10
= ; 2
75
0,75 10
−
−= ; 0
12
12 10
=
( Les entiers sont des décimaux )
ATTENTION : tout nombre à virgule n’est pas un nombre décimal,
En effet 1
3= 0,3333333… n’est pas dans ID
Il ne se « finit pas après la virgule » …
# D vient du français : « Décimale ».
D
0,0004
2,5
-0,75
123,5348
12
Rationnels Ce sont les nombres qui peuvent s’écrire sous la forme p
q
avec p et q entiers relatifs.
Tous les décimaux sont des rationnels ; ex : 123
12,3 10
=.
De Z à Q : solution de l’équation a x = b.
introduit dans l’antiquité.
# Q vient de l’italien : « Quotiente ».
Q
12
13
7
38
−
1,5
...
Réels Ce sont tous les nombres que nous utilisons et que nous représentons
sur un axe gradué. Certains réels ne sont pas des rationnels ;
ex : 2 ,
π
, e , ... ( On dit qu’ils sont irrationnels )
De Q à IR : solution de l’équation x 2 = a , avec a >0
introduit par les Grecs avec Pythagore, Aristote, Euclide.
# R vient de l’allemand : « Real »
R
32,542
4 3
π
…

On a et on note :
N
⊂
Z
⊂
D
⊂
Q
⊂
R
( inclus) et 102
∈
N
( appartient ).
N Z D Q R
102
2
3
-27
0,02 17
Remarque : Il existe encore des équations que l’on ne peut pas résoudre dans IR.
Ex : , …
21x=− 240x+=
Ces équations ont pourtant des solutions dans un ensemble noté C ( ensemble des nombres complexes ),
plus grand que R…
Rendez-vous en 1e ou en terminale ….
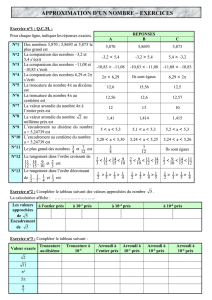
II – VALEUR EXACTE, VALEURS APPROCHEES
La troncature à n chiffres d’un nombre ( n entier naturel ) est obtenue en ne conservant que les
n premiers chiffres après la virgule.
L’arrondi à la précision n
10
−
d’un nombre est obtenue à partir de sa troncture à n chiffres :
- si le (n+1)e chiffre est égal à 0,1,2,3 ou 4, alors l’arrondi est égal à la troncature à n chiffres ;
- si le (n+1)e chiffre est égal à 5,6,7,8 ou 9, alors le n-ième chiffre après la virgule est augmenté de 1.
Exemples :
( A COMPLETER ) 8,569 201 324 π ≈ 3,141 592 653 589… 23
7≈ 3,285 714 285 714…
Valeur exacte
Troncature à 2 chiffres
Troncature à 3 chiffres
Arrondi à l’unité
Arrondi à 10-2
Arrondi à 10-2
par défaut
Arrondi à 10-2
par excès
Arrondi à 10-3
Arrondi à 10-3
par défaut
Arrondi à 10-3
par excès
Les troncatures et les arrondis sont des valeurs approchées des nombres.

III - ECRITURE SCIENTIFIQUE - ORDRE DE GRANDEUR
a. Ecriture scientifique
La notation scientifique d’un nombre
x
est l’écriture de ce nombre sous la forme :
p
a10x=± × ,
où a est un nombre décimal tel que 1a10
≤
<, et p un entier relatif ( positif ou négatif )
Exemples :
Nombres Ecriture scientifique
358,1 3,581 ×
2
10
- 480 000 - 4,8 ×
5
10
0,0005 5 ×
4
10−
52 × 4
10
−
5,2 ×
3
10
−
423 ×
5
10 4,23 ×
7
10
b. Ordre de grandeur
L’ordre de grandeur d’un nombre est le nombre sous la forme :
p
m10×,
où m entier relatif (-10 < a < 10) et p entier relatif. On a alors
p
m10x×≈
On l’obtient facilement à partir de l’écriture scientifique du nombre.
Exemples :
8 269 201 324 0,000 052 932 - 58 345 943
Ecriture scientifique 8,269 201 324 × 109 5,293 2 × 10-5 -5,834 594 3 × 107
Ordre de grandeur 8 × 109 5 × 10-5 -6 × 107
c. La calculatrice
La calculatrice ne manipule que des nombres décimaux.
En outre, elle ne peut afficher qu’un nombre limité de chiffres (les « digits ») sur son écran
(généralement entre 8 et 12). Quand elle ne peut pas afficher la valeur exacte d’un nombre,
elle la remplace par une valeur approchée.
Exemples :
20
3 = 20 ÷ 3 ≈ 6,666 666 666 …
9999 = 991 035 916 125 874 083 964 008 999 ≈ 9,910 359 161 E 26
INFO TI82 :
Pour mettre un résultat en fraction : MATH Frac ENTER
Ex : taper 1/3 + 2/5 …. La calculatrice donne 0.733333…
Mettre le résultat en fraction, et vérifier par le calcul.
On trouve 11/15 ;
12 5 6 11
3 5 15 15 15
+
=+=

IV – NOMBRES PREMIERS
a. Diviseurs d’un nombre
Définition :
Soit a et b deux nombres entiers.
On dit que b est un diviseur de a (ou alors a est divisible par b) si a
b
est un nombre entier.
Exemples :
2 est un diviseur de 98
100 est un diviseur de 1 500.
Remarque : tout nombre entier (distinct de 0 et 1) admet au moins 2 diviseurs : 1 et lui-même.
Critères de divisibilité
2 S’il se termine par un chiffre pair
3 Si la somme de ses chiffres est divisible par 3
4 Si le nombre formé par ses deux derniers chiffres est divisible par 4
5 S’il se termine par 0 ou 5
6 S’il est divisible par 2 et par 3
7 On prend tous les chiffres sauf le dernier ( 3 chiffres minimum )
On soustrait 2 fois le dernier
On vérifie si le résultat est divisible par 7
8 Si le nombre formé par ses trois derniers chiffres est divisible par 8
9 Si la somme de ses chiffres est divisible par 9
Un nombre
est
divisible
par :
10 Si le chiffre des unités est 0
b. Nombre premier
Définition :
Un
nombre premier est un entier naturel strictement supérieur à 1, n'admettant que deux
diviseurs distincts: 1 et lui-même.
Exemples : 2 ; 3 ; 5 ; 7 ; 11 ; 13…
c. Décomposition d’un nombre en produit de facteurs premiers
Théorème :
Tout entier naturel strictement supérieur à 1 est premier ou produit de nombres (facteurs) premiers.
Exemple : 35 n’est pas premier. Mais 35 = 5 × 7, les facteurs 5 et 7 étant premiers.
Méthode : Pour décomposer un nombre en produits de facteurs premiers, on peut : présentation
• Essayer de diviser le nombre par 2 et, si c’est possible, le quotient par 2, 600 2
et recommencer tant que c’est possible ; 2 300
• Faire la même chose avec 3, etc … 2 150
• Recommencer avec chacun des nombres premiers 5 ,7 ,11, … 75
• On s’arrête lorsque le quotient est 1. 25
5
On a : 32
600 2 3 5
=
×× . 1
3
5
5

Corrigé
Exemples :
( COMPLETE ) 8,569 201 324 π ≈ 3,141 592 653 589… 23
7≈ 3,285 714 285 714…
Valeur exacte 8,569 201 324
π
23
7
Troncature à 2 chiffres 8,56 3,14 3,28
Troncature à 3 chiffres 8,569 3,141 3,285
Arrondi à l’unité 9 3 3
Arrondi à 10-2 8,57 3,14 3,29
Arrondi à 10-2
par défaut 8,56 3,14 3,28
Arrondi à 10-2
par excès 8,57 3,15 3,29
Arrondi à 10-3 8,569 3,142 3,286
Arrondi à 10-3
par défaut 8,569 3,141 3,285
Arrondi à 10-3
par excès 8,570 3,142 3,286
 6
6
 7
7
1
/
7
100%