1
Filtres passe-bas
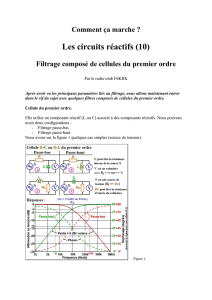
Ce court document expose les principes des filtres passe-bas, leurs
caractéristiques en fréquence et leurs principales topologies. Les
éléments de contenu sont :
• Définition du filtre passe-bas
• Fonction de transfert et réponse en fréquence
• Topologies courantes
• Filtres passe-bas d’ordres supérieurs
• Filtres anti-alias
Définition du filtre passe-bas
Le filtre passe-bas est un dispositif qui démontre une réponse en
fréquence relativement constante (gain fixe) aux basses fréquences
et un gain décroissant aux fréquences supérieures à la fréquence de
coupure. La décroissance plus ou moins rapide dépend de l’ordre
du filtre.
Idéalement, le filtre passe-bas aurait un gain unitaire (ou fixe) aux
basses fréquences et un gain nul aux fréquences supérieures à la
coupure « fo » :
f (hz)
Gain
(lin.)
0
1
fo
0
log(f)
Gain
(db)
-∞
0fo
On utilise les filtres passe-bas pour réduire l’amplitude des compo-
santes de fréquences supérieures à la celle de la coupure.
t
Vin
t
Vout
Filtre
passe-bas
Ordre du filtre
En pratique, il est impossible d’obtenir une caractéristique aussi
parfaite que celle illustrée précédemment. En effet, on ne peut que
Oct 06 Jude Levasseur

2 FILTRES PASSE-BAS
se rapprocher de celle-ci en augmentant l’ordre du filtre. Ce der-
nier correspond grosso modo aux nombres d’étages d’éléments
réactifs c.a.d. de composantes dont l’impédance varie avec la fré-
quence.
On distingue l’ordre du filtre par la pente de réponse en fréquence
aux fréquences supérieures à la coupure. Cette pente est de « n fois
-20db/decade » où « n » représente l’ordre du filtre.
0.1 1 10
Ordre de filtre passe-bas
Fréquences (f / fo)
Gain (db)
50
40
30
20
10
0
10
60
n = 10
n = 8
n = 6
n = 4
n = 1
n = 2
Note :
• Une pente de -20db/décade équivaut à une pente de -6db/octave ou un oc-
tave correspond à doubler la fréquence.
•
(
)
db Gain
Gain db
=⋅
=
20
1020
log
• Un gain de 0 db correspond à un gain linéaire de 1 (unitaire)
• Un gain > 0db correspond à un gain linéaire > 1 (amplification)
• Un gain < 0db correspond à un gain linéaire < 1 (atténuation)
• Valeurs utiles à retenir :
Gain
(db) -60 -40 -20 -6 -3 0 3 6 20 40 60
Gain
(linéaire) 0,001 0,01 0,1 0,5 0,707 1 1,41 2 10 100 1000
Oct. 06 Jude Levasseur

FILTRE PASSE-BAS DU PREMIER ORDRE 3
Filtre passe-bas du premier ordre
Le filtre passe-bas du premier ordre est défini par la fonction de
transfert suivante :
()
FT f
jf
f
lp
o
11
1
≡⎛
⎝
⎜⎞
⎠
⎟+
où « fo » est la fréquence de coupure (ou
du pôle).
0.01 0.1 1 10 100
40
20
03
dbi
fi
fo
0.01 0.1 1 10 100
90
45
0
.
phase ideg 1
fi
fo
L’implantation du filtre du premier ordre s’effectue à l’aide d’un
simple circuit RC :
Circuit RC
R1
C1
Vi Vo
La fréquence de coupure correspond à :
fRC
o=1
211
π
Oct. 06 Jude Levasseur

4 FILTRES PASSE-BAS
Si l’on veut ajouter un gain au filtre de premier ordre, on peut
choisir l’un ou l’autre des montages suivants :
Ajout d’un gain
Le gain statique ( f << fo ) :
R1
C1
Vi
Ra Rb
Vo
KRb
R
a
=+1
La fréquence de coupure :
fRC
o=:1
211
π
Le gain statique ( f << fo ) :
Vi
R1
R2
Vo
C1
KR
R
=− 2
1 (inverseur)
La fréquence de coupure :
fRC
o=:1
221
π
Filtre passe-bas du second ordre
Le filtre passe-bas du second ordre est défini par la fonction de
transfert suivante :
()
FT f
jf
fjQf
f
lp
oo
2
2
21
11
≡⎛
⎝
⎜⎞
⎠
⎟+⎛
⎝
⎜⎞
⎠
⎟+
Les paramètres « fo » et « Q » sont respectivement la fréquence du
pôle et le facteur de qualité.
Le facteur « Q » influence la forme du coude de la réponse en fré-
quence. Un facteur Q de 0,5 correspond à la mise en cascade de
deux circuits RC identiques et séparés par un suiveur.
Pour des facteurs « Q » supérieurs à 0,707 (>22)
, il existe une
fréquence pour laquelle le gain est maximal. On dit alors qu’il
existe une pseudo-résonnance. La fréquence (fgmax) et le gain
(Gmax) de cette pseudo-résonnance sont :
ff Q
gmax o
=⋅−11
22 et GQ
Q
max =−1142
Oct. 06 Jude Levasseur

FILTRE PASSE-BAS DU SECOND ORDRE 5
0.1 1 10
40
20
0
20
Gain (db)
3
fi
fo
Q=10
Q=5
Q=2
Q=1
Q=0,5
Q=0,707
0.1 1 10
180
135
90
45
0
Phase (deg.)
fi
fo
Q=10
Q=5
Q=2
Q=1
Q=0,5
Q=0,707
L’implantation passive du filtre du second ordre s’effectue à l’aide
d’un simple circuit RLC :
Circuit RLC
fLC
o=1
211
π
R1
C1
Vi Vo
L1
QRL
C
=1
1
1
1
Oct. 06 Jude Levasseur
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
 16
16
1
/
16
100%