Lorsqu’on veut
comparer ou calculer des longueurs, on doit d’abord les
exprimer dans la même unité. On dit qu’on les convertit.
1 km = 1 000 m
1 m = 100 cm
1 m = 1 000 mm
1 cm = 10 mm
km = kilomètre
hm = hectomètre
dam = décamètre
m= mètre
dm = décimètre
cm = centimètre
mm = millimètre
Multiples
du mètre
mètre
Sous-multiples
du mètre
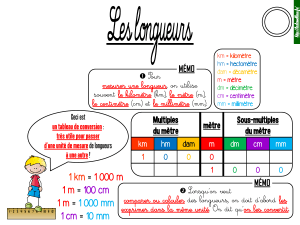
km hm dam mdm cm mm
1000
1000
Pour
mesurer une longueur, on utilise
souvent le kilomètre (km), le mètre (m),
le centimètre (cm) et le millimètre (mm).
Ceci est
un tableau de conversion :
très utile pour passer
d’une unité de mesure de longueurs
à une autre !

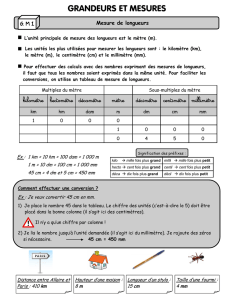
Lorsqu’on veut
comparer ou calculer des longueurs, on doit d’abord les
exprimer dans la même unité. On dit qu’on les convertit.
1 km = 1 000 m
1 m = 100 cm
1 m = 1 000 mm
1 cm = 10 mm
km = kilomètre
hm = hectomètre
dam = décamètre
m= mètre
dm = décimètre
cm = centimètre
mm = millimètre
Multiples
du mètre
mètre
Sous-multiples
du mètre
km hm dam mdm cm mm
1000
1000
Pour
mesurer une longueur, on utilise
souvent le kilomètre (km), le mètre (m),
le centimètre (cm) et le millimètre (mm).
Ceci est
un tableau de conversion :
très utile pour passer
d’une unité de mesure de longueurs
à une autre !

3 cm
côté X4
cX4
3X4= 12 cm
7 cm
3 cm
(Longueur + largeur) X2
(L+ l) X2
(7+3)X2= 20 cm
A
B
D7 cm
P = 5+ 3+ 7+ 4
P = 19
Le périmètre
de ce polygone est de 19 cm.
C
La longueur
du contour d’une figure s’appelle le périmètre.
On calcule
le périmètre d’un polygone en
additionnant la longueur de tous ses côtés.
Pour certains polygones,
on utilise des formules pour simplifier les calculs.

1 g = 10 dg = 100 cg = 1 000 mg
1 kg = 10 hg = 100 dag = 1 000 g
Multiples
du gramme
gramme
Sous-multiples
du gramme
kg hg dag gdg cg mg
1000
kg = kilogramme
hg = hectogramme
dag = décagramme
g= gramme
dg = décigramme
cg = centigramme
mg = milligramme
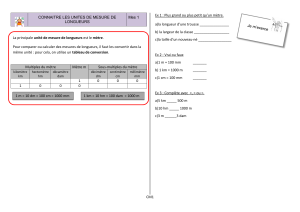
Les
autres unités
de mesure de masses sont :
•le quintal (q) = 100 kg
•la tonne (t) = 1 000 kg
L’unité de mesure des masses est le gramme.
Avant d’effectuer
des calculs sur les masses,
il faut les exprimer dans la même unité.

1 g = 10 dg = 100 cg = 1 000 mg
1 kg = 10 hg = 100 dag = 1 000 g
Les
autres unités
de mesure de masses sont :
•le quintal (q) = 100 kg
•la tonne (t) = 1 000 kg
L’unité de mesure des masses est le gramme.
Avant d’effectuer
des calculs sur les masses,
il faut les exprimer dans la même unité.
Multiples
du gramme
gramme
Sous
-
multiples
du gramme
t q
kg
hg
dag g
dg
cg
mg
1000
t = tonne
q = quintal
kg = kilogramme
hg = hectogramme
dag = décagramme
g= gramme
dg = décigramme
cg = centigramme
mg = milligramme
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
1
/
15
100%