Machine asynchrone
Machine asynchrone
diagramme du cercle
diagramme du cercle
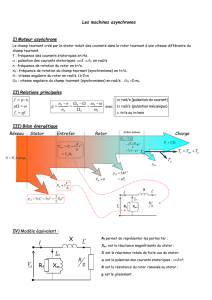
La machine asynchrone est un transformateur à
champ tournant.
Soit I1 le courant d ’une phase statorique,
soit I2 le courant d ’une phase rotorique.
Ces courants engendrent des
forces magnétomotrices tournantes de
vitesse Ns : n’1I1 et n’2I2, n’1et n’2 étant les
nombres de spires de chaque enroulement
corrigés par les coefficients de Kapp.
R1
I1F I10
n’1
I1
l1
stator = primaire
R2
n’2
l2
rotor = secondaire
0 = j n ’2ω φ - j ω l2 I2 - R2 I2
g
V1 = j n ’1ω φ + j ω l1 I1 + R1 I1
Pour une phase du stator :
V2 = 0 = j n ’2(gω) φ - j (gω) l2 I2 - R2 I2
Pour une phase du rotor :
R1
I1F I10
n’1
I1
l1
stator = primaire
R2
n’2
l2
rotor = secondaire
ωgω
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
1
/
44
100%
