MécaniqueSolides Chapitre 15

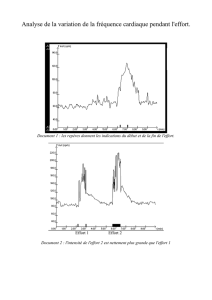
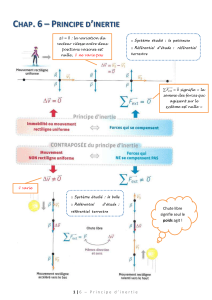
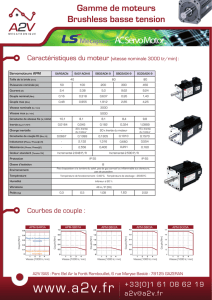
Partie IV
Cinétique des Solides
La cinématique des solides s'est intéressée au mouvement des solides
sans se préoccuper des masses à déplacer. Or il est plus facile de
déplacer à une vitesse donnée un solide de faible masse qu’un solide
de masse élevée. Il est donc nécessaire d'introduire des concepts qui
associent mouvement des solides et masse des solides. Ces concepts
sont basés sur l'introduction des notions de torseur cinétique, torseur
dynamique et énergie cinétique.

CHAPITRE 15
L'opérateur d'inertie
La notion d'opérateur d'inertie que nous étudions dans ce chapitre, permettra
d'exprimer simplement les divers torseurs (Chapitre 16) nécessaires à l'étude de la
dynamique des solides.
15.1 INTRODUCTION DE L'OPÉRATEUR D'INERTIE
15.1.1 Opérateur associé à un produit vectoriel
Considérons deux vecteurs a
G
et V
J
G, dont les composantes dans la base (b) =
(
)
, , ijk
G
GG sont :
, .
xyz
aaiajak V XiYjZk=++ =++
G
G
J
G
GG GG
G (15.1)
Le produit vectoriel des deux vecteurs s'écrit :
()
(
)
(
)
yz z x xy
aV aZaYi aX aZj aY aXk∧= − + − + −
G
J
G
G
G
G. (15.2)
Si le vecteur a
G est un vecteur donné, nous constatons, que quel que soit le vecteur
V
JG , nous passons de V JG au vecteur aV
∧
J
G
G
par une opération linéaire. En effet, nous
avons :
(
)
(
)
()
3
3
12 1 2 1 2
et , ,
, , .
VaVaV
VV a V V a V a V
λλλ ∀∈ ∀∈ ∧ = ∧
∀∈ ∧+=∧+∧
JG JG JG
G
G
\\
JJGJJGJJGJJGJJGJJG
GGG
\ (15.3)
Il revient alors au même de dire que l'on passe du vecteur V
J
G au vecteur aV∧JG
G, en
faisant agir sur V
J
G un opérateur linéaire A et d'écrire que :
.aV V∧=
J
GJG
G
A (15.4)
Sous forme matricielle, l'expression (15.2) du produit vectoriel s'écrit dans la

228 Chapitre 15 L'opérateur d'inertie
base
(
)
, , ijk
G
GG
:
0
0
0
yz zy
zx z x
xy yx
aZ aY a a X X
aX aZ a a Y Y
aY a X a a Z Z
−−
⎡
⎤⎡ ⎤⎡⎤ ⎡⎤
⎢
⎥⎢ ⎥⎢⎥ ⎢⎥
−= − =
⎢
⎥⎢ ⎥⎢⎥ ⎢⎥
⎢
⎥⎢ ⎥⎢⎥ ⎢⎥
−−
⎣
⎦⎣⎦
⎣⎦⎣ ⎦
A, (15.5)
en introduisant la matrice antisymétrique :
0
0
0
zy
zx
yx
aa
aa
aa
−
⎡
⎤
⎢
⎥
=−
⎢
⎥
⎢
⎥
−
⎣
⎦
A. (15.6)
A est la matrice qui représente l'opérateur A (ou le produit vectoriel a∧
G), dans la
base (b) =
()
, , ijk
G
GG .
Lorsqu'il n'y a qu'une base en jeu, la notation A n'est pas ambiguë. Par contre,
s'il y a plusieurs bases, il sera nécessaire de préciser la notation, en écrivant par
exemple : A(b), matrice représentant l'opérateur A dans la base (b).
15.1.2 Extension du résultat précédent
Nous cherchons à déterminer maintenant le double produit vectoriel
()
aaV∧∧
JG
GG . D'après le paragraphe précédent, nous pouvons écrire :
()
(
)
2
aaV a V V V∧∧ =∧ = =
JG JG JG JG
GG G
AAAA. (15.7)
Le nouvel opérateur 2 A ainsi introduit est un opérateur linéaire. Il est repré-
senté par la matrice A2 dans la base
(
)
, , ijk
G
G
G
:
()
()
()
22
222
22
yz xy xz
xy x z yz
x
zyzxy
a a aa aa
aa a a aa
aa aa a a
⎡⎤
−+
⎢⎥
⎢⎥
=−+
⎢⎥
⎢⎥
−+
⎣⎦
A . (15.8)
La matrice A2 est une matrice symétrique.
De même, nous pouvons écrire :
()
(
)
2
aVa aaV V V∧∧=−∧∧=− =
JG JG JG JG
GGGG
AB, (15.9)
où l'opérateur 2
=
− BA est représenté par la matrice 2
=
−BA :
22
22
22
yz xy xz
x
yxz yz
x
zyzxy
aa aa aa
aa a a aa
aa aa a a
⎡⎤
+− −
⎢⎥
=− + −
⎢⎥
⎢⎥
−− +
⎢⎥
⎣⎦
B. (15.10)

15.1 Introduction de l'opérateur d'inertie 229
FIGURE 15.1. Solide.
15.1.3 Opérateur d'inertie
Dans l'évaluation (Chapitre 16) des torseurs utilisés en dynamique, nous aurons
à exprimer des vecteurs de la forme :
()
()
1d( )
S
WOMVOMmM=∧∧
∫
JJG JJJJG JG JJJJG, (15.11)
()
[]
()
2d( )
S
WOMVVOMmM=∧∧∧
∫
JJG JJJJG JG JG JJJJG. (15.12)
Les intégrales sont calculées sur le solide (S) (linéique, surfacique ou
volumique). Le point M (figure 15.1) est un point variable de (S), et d( )mM est la
masse de l'élément de (S) entourant le point M. Le point O est un point de
référence du solide (S). Le vecteur V
J
G est indépendant du point M.
D'après les résultats établis au paragraphe précédent, nous pouvons écrire :
()
1O
WSV=
J
JGJG
I, (15.13)
en introduisant l'opérateur
()
OSI, appelé opérateur d'inertie en O du solide (S).
Cet opérateur est représenté dans une base (b) liée au solide par une matrice
()
()
b
OSI, appelée matrice d'inertie en O et dans la base (b), du solide (S). Nous
l'écrivons suivant l'une des formes :
()
()
Ox Oxy Oxz
b
O Oxy Oy Oyz
Oxz Oyz Oz
AFE I P P
SFBDPI P
EDC P P I
−− − −
⎡⎤⎡ ⎤
⎢⎥⎢ ⎥
=− − =− −
⎢⎥⎢ ⎥
⎢⎥⎢ ⎥
−− − −
⎣⎦
⎣
⎦
I. (15.14)
Si (x,y,z) sont les coordonnées cartésiennes du point M dans le trièdre
()
/Ob=
(Oxyz), nous avons :
y
z
x
O
d m(M)
M
k
G
(S)
j
G
i
G