TP Ondes Ultrasonores: Vitesse, Incertitudes & Interférences
Telechargé par
Ayoub Talibi

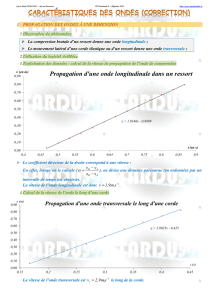
TP Ondes ultrasonores.
Mesure de la vitesse d’une onde. Incertitudes.
Matériel : nous disposons ici d’émetteurs d’ondes sonores qui fonctionnent à la fréquence 40 kHz (ultra sons).
Lorsqu’un émetteur est alimenté par un GBF (générateur « basses fréquences ») réglé sur cette fréquence, une
conversion électromécanique (composant piézoélectrique) permet la génération d’onde. Par le procédé inverse
(capteur piézoélectrique) le récepteur donne une tension à l’image de l’onde ultrasonore au point où il est situé.
1- Détermination de la vitesse des ondes ultrasonores dans l’air par la méthode des impulsions
1-1 Présentation :
Le GBF peut générer des salves en mode « burst ». Une salve ou train d’onde est un certain nombre de période
(ou cycles) de sinusoïdes. Les salves sont séparées entre elles d’une durée que l’on peut fixer.
Le GBF émettra à partir de la voie 1(Output CH1 doit être allumée)
Dans chaque salve, la fréquence des sinusoïdes doit être de 40 kHz (fréquence réglée sur le GBF).
L’amplitude « crête à crête » (ou « peak-peak ») des salves est fixée par V
pp
. Nous prendrons V
pp
= 6V (le signal
variera alors de -3V à +3V).
Le nombre de cycles est le nombre de période dans chaque salve (4 périodes ou cycles dans l’exemple ci-
dessus), pour notre manipulation nous le fixerons à 100 cycles pour chaque salve.
Dans le mode Burst l’onglet « période » permet de fixer la périodicité des salves (à ne pas confondre avec la
période des sinusoïdes). Nous prendrons « période » = 5 ms.
Une série de salves est générée par l’émetteur et le signal est capté par le récepteur placé un peu plus loin.
Une règle métallique nous permet de repérer les positions de l’émetteur et du récepteur.
Nous cherchons à déterminer le temps de parcours de l’onde. Notons qu’une importante incertitude existe sur la
position de la cellule piézoélectrique dans le récepteur et dans l’émetteur.
« période » des salves
t
signal délivré
par le GBF
« salve » : portion de sinusoïde de
fréquence f = 40 kHz
V
pp
T =
f
1
Période des
sinusoïdes
Burst « activé »
si le bouton est
allumé
Attention output doit être
allumée pour que la voie 1
(CH1) soit active.
Les salves sont
des sinusoïdes
Réglage
fréquence Réglage
amplitude Réglage valeur moyenne (nulle
pour cette manipulation)
GBF utilisé :
Réglage des caractéristiques
du signal CH1 ou du signal
CH2 (pour nous ici CH1)

1-2 Manipulation
1-2-a) Mesure de la vitesse du son dans l’air :
La synchronisation de l’oscilloscope est difficile dans le mode « Burst », cela signifie que l’image est instable à l’écran.
On utilisera alors le mode RUN/STOP de l’oscilloscope pour « figer » les signaux.
Horiz : Activer pour
Passage en
mode XY
Synchronisation et
déclenchement du
signal
Les voies allumées
s’affichent à l’écran
(cliquer pour éteindre
ou allumer)
Echelle
automatique
Echelle horizontale
(« nombre de seconde
par carreau »)
Déplacement
« horizontaux »
des signaux à
l’écran
RUN/STOP :
Pour figer
une image à
l’écran
Activer les
curseurs
Déplacement des
curseurs. Cliquer
pour valider et figer
le curseur
Rappels sur
l’oscilloscope utilisé :
signal 2
(vert)
signal 1
(jaune) mesures sur les
signaux
(fréquences,
valeurs efficaces...)
Echelle
verticale
(nombre de
Volts par carreau)
Déplacements
« verticaux » des
signaux à l’écran
Déplacement dans les
différents menus,
(menu déroulant en
tournant puis cliquer
pour valider)
Niveau de
déclenchement
valeurs des
mesures
(périodes,
fréquences,
valeurs
efficaces...)
.
Retard à la propagation (à
mesurer grâce aux curseurs)
Salves émises
Signal capté
par le récepteur
Les signaux étudiés auront
l’aspect suivant :

Pour une valeur de « x » que vous choisirez estimer « t » puis « c » vitesse du son dans l’air.
La mesure de « t » se fera grâce aux curseurs (Allumer « cursors » puis les déplacer grâce aux fonctions prévues
sur l’oscilloscope. Les curseurs doivent être réglés en type temps. Dans ce mode les curseurs sont des barres
verticales qui repèrent des durées).
1-2-b) Incertitudes de mesures.
Estimer l’incertitude sur le distance « x » (notée ∆x) ainsi que l’incertitude sur la durée « t » (notée ∆t)
1-2-c) En déduire une incertitude sur la mesure de la vitesse c.
Remarque 1 :
( )
²x.
x
c
c
2
x
∆
∂
∂
=∆
est l’incertitude sur c liée à x
( )
²t.
t
c
c
2
t
∆
∂
∂
=∆
est l’incertitude sur c liée à t on a donc :
( ) ( )
2
t
2
x
ccc ∆+∆=∆
Remarque 2 : plutôt que d’utiliser
²t.
t
c
²x.
x
c
c
22
∆
∂
∂
+∆
∂
∂
=∆
nous pouvons utiliser le fait que lorsque l’on a
une formule du type
γ
βα
=
3
21
x
x.x
G
on peut écrire
2
3
3
2
2
2
2
1
1
x.
x
x.
x
x.
x
.GG
∆
γ
+
∆
β
+
∆
α
=∆
Dans notre cas, cela donne : avec
t
x
c=
22
t.
t
1
x.
x
1
.cc
∆+
∆=∆
Cela nous évite de calculer des dérivées partielles.
Emetteur Récepteur
x

1-2-d) Mesurer 3 nouvelles valeurs de t pour 3 nouvelles valeurs de x différentes.
En déduire une nouvelle mesure de c par régression linéaire (on fera apparaitre les ellipses d’incertitudes sous
« regressi »).
2- Détermination de la vitesse de propagation à partir de la mesure de la longueur d’onde
Nous allons ici estimer la longueur d’onde d’une onde plane sinusoïdale ultra sonore et, connaissant sa
fréquence, nous en déduirons la vitesse de propagation.
On utilise donc à présent le GBF en mode sinusoïdal de fréquence 40 kHz. Pour minimiser le « bruit »
(perturbations électriques) par rapport au signal nous prendrons une amplitude assez importante (par exemple 6V
crête à crête).
On veut mesurer la longueur d’onde des ondes acoustiques. Les phases de l’onde sonore au niveau de l’émetteur
et du récepteur ne sont pas les mêmes. Le déphasage entre les signaux électriques correspondants varie
périodiquement avec la distance entre l’émetteur et le récepteur. La périodicité est λ. Lorsque l’émetteur et le
récepteur sont distants d’un multiple entier de la longueur d’onde λ les signaux sont en phase.
Lorsque les signaux sont en phase il faut un déplacement minimum du récepteur d’une distance λ pour qu’ils se
retrouvent à nouveau en phase.
2-1 Mesure de la longueur d’onde en mode temporel
2-1-a) Mesurer la distance séparant une vingtaine de coïncidences de phase et en déduire une mesure de la
longueur d’onde λ du signal.
2-1-b) Donner une estimation de l’incertitude sur λ (notée ∆λ)
2-1-c) En déduire une mesure de la vitesse « c » de propagation de l’onde.
2-1-d) Donner une estimation de l’incertitude ∆c sur la mesure de c sachant que d’après le constructeur de
l’appareil l’incertitude sur la fréquence du signal est ∆f ≈ 1 Hz.
Nous avons c/f = λ donc c = λ.f il s’agit bien d’une forme :
γ
βα
=
3
21
x
x.x
G
, (avec par exemple x
1
= λ, α = 1, x
2
= f,
β = 1, x
3
quelconque car γ = 0) on peut utiliser
2
3
3
2
2
2
2
1
1
x.
x
x.
x
x.
x
.GG
∆
γ
+
∆
β
+
∆
α
=∆
qui donne ici
22
cc
λ
λ∆
+
νν∆
=∆

Remarque on peut aussi utiliser
f.c
λ
=
→
f
c=
λ∂
∂
et
λ=
∂
∂f
c
ce qui nous donne une incertitude composée
²f.².f²f.
f
c
².
c
c
22
22
∆λ+λ∆=∆
∂
∂
+λ∆
λ∂
∂
=∆
→
²f.².fc
22
∆λ+λ∆=∆
2-2- Mesure de la longueur d’onde en mode XY
2-2-a) Mesurer la distance séparant une vingtaine de coïncidences de phase en mode XY (signal délivré par le
GBF en abscisse et signal délivré par le récepteur en ordonnée) et en déduire une mesure de la longueur d’onde
λ du signal.
Rappel : lorsque les signaux sont déphasés, on visualise une ellipse, lorsqu’ils sont en phase, on visualise une
droite de pente positive (en opposition de phase, on visualise une droite de pente négative).
2-2-b) Donner alors l’incertitude ∆λ associée.
2-2-c) En déduire une mesure de la vitesse « c » de propagation de l’onde ainsi que l’incertitude ∆c sur cette
mesure.
voie 2 (GBF)
voie 1 (récepteur)
voie 2 (GBF)
voie 1 (récepteur)
Déphasage quelconque Signaux en phase
 6
6
 7
7
1
/
7
100%