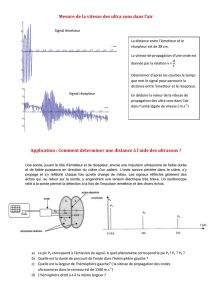
Propagation d`une onde longitudinale dans un

Lycée Paul CEZANNE – Aix-en-Provence TP Terminale S – Réforme 2012 http://www.stardustlabs.fr
 La compression brutale d’un ressort donne une onde longitudinale ;
 Le mouvement latéral d’une corde élastique ou d’un ressort donne une onde transversale ;
 Le coefficient directeur de la droite correspond à une vitesse :
En effet, lorsqu’on le calcule (
BA
BA
yy
xx
), on divise une distance parcourue (en ordonnée) par un
intervalle de temps (en abscisse).
La vitesse de l’onde longitudinale est donc
1
v 1,9m.s
.
La vitesse de l’onde transversale est
1
c
v 2,9m.s
le long de la corde.
y = 1,9346x - 0,8809
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
0,4 0,45 0,5 0,55 0,6 0,65 0,7 0,75 0,8 0,85 0,9
x (en m)
t (en s)
Propagation d'une onde longitudinale dans un ressort
y = 2,9025x - 0,425
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
0,15 0,2 0,25 0,3 0,35 0,4 0,45
x (m)
t (s)
Propagation d'une onde transversale le long d'une corde

Lycée Paul CEZANNE – Aix-en-Provence TP Terminale S – Réforme 2012 http://www.stardustlabs.fr
Activer les voies EA0 et EA2 sur Oscillo5 (on visualise alors le signal de l’émetteur et le signal d’un récepteur).
 Comparer qualitativement les deux signaux. Le signal reçu dépend-il de la position du récepteur ?
Le signal reçu dépend de la position du récepteur : il a la même période que le signal émis par le
récepteur mais il est plus ou moins déphasé selon sa position, et son amplitude diminue quand la
distance entre l’émetteur et le récepteur augmente.
 L’onde ultrasonore est dite progressive et périodique. Expliciter brièvement ces deux termes.
L’onde ultrasonore est progressive car elle se déplace de l’émetteur vers le récepteur. Elle est
périodique car elle se reproduit à l’identique et à intervalle de temps régulier.
 Déterminer la période des signaux émis et reçus sur l’écran de l’oscilloscope. Les comparer.
On a représenté la durée correspondant à 5 périodes (en rouge) : il s’agit de la même durée pour
l’émetteur et pour le récepteur. Ces 5 périodes s’affichent sur 12,4 divisions, on a donc :
65
12,4 10.10
T 2,5.10 s
5
 Déterminer l’incertitude U(T) sur la mesure de la période (voir fiche n°3 p. 584).
On peut considérer qu’on effectue une simple mesure (le déclenchement se fait à 0V dans le sens
montant, donc on ne mesure pas à gauche), l’incertitude s’écrit alors :
2 0,2 10
U T 1 s
12

Lycée Paul CEZANNE – Aix-en-Provence TP Terminale S – Réforme 2012 http://www.stardustlabs.fr
En déduire la fréquence des ondes ultrasonores et un encadrement de cette fréquence, sachant que
l’incertitude sur la fréquence est donnée par
U(T)
U(f)= f T
:
4
5
11
f 4,0.10 Hz
T 2,5.10
L’incertitude sur f s’écrit
Hz
-6
43
-5
1.10
U(f)= 4,0.10 1,6.10
2,5.10
La valeur de la fréquence avec son incertitude mesurée s’écrit donc :
43
f 4,0.10 1,6.10 Hz 40 1,6kHz   
Cet encadrement est compatible avec la valeur indiquée par le constructeur (38,5 kHz à 41,5 kHz).
Repérer les positions du récepteur pour lesquelles les signaux sont en phase.
 Comment peut-on visualiser la longueur d’onde λ avec un tel dispositif ?
On place les deux récepteurs côte à côte de manière à ce que les signaux qu’ils reçoivent soient en
phase. On recule un récepteur jusqu’à ce que les deux signaux soient de nouveau en phase (les deux
points M et M’ représentés par les micros sont donc dans le même état en même temps) : la distance
entre les deux récepteurs représente la longueur d’onde des ultrasons émis.
 Déterminer la longueur d’onde de l’onde ultrasonore dans l’air à la température de la salle.
On mesure la distance correspondant à 10 longueurs d’ondes, on obtient
d 160 75 85mm  
;
Donc
d 85 8,5mm
10 10
 Évaluer l’incertitude U( ) sur cette mesure (voir fiche n°3 p. 584). Écrire la longueur d’onde sous la
forme d’un encadrement.
On effectue une double mesure, l’incertitude s’écrit donc
21
U d 2 0,8mm 1mm
12
;
Remarque : en réalité, cette incertitude est plus grande, car à l’incertitude de lecture des
graduations de la règle s’ajoutent celles dues à la lecture sur l’écran de l’oscilloscope, la mesure
de la température de la pièce, la pression, la vitesse du son, etc.
L’incertitude sur une période spatiale est aussi divisée par 10, puisqu’on a mesuré une distance
correspondant à 10 λ :
Ud 1
U' d 0,1mm
10 10
L’encadrement de la longueur d’onde est donc
8,4mm 8,6mm

Lycée Paul CEZANNE – Aix-en-Provence TP Terminale S – Réforme 2012 http://www.stardustlabs.fr
 Pourquoi est-il préférable de mesurer dix longueurs d’onde plutôt qu’une seule ?
Si l’on n’avait mesuré qu’une seule longueur d‘onde, l’incertitude aurait été
U d 1mm
et la
mesure de λ aurait été moins précise sur la règle graduée (
158 150 8mm
). On aurait alors eu
l’encadrement :
7mm 9mm
C’est un encadrement nettement moins bon !
 Évaluer la célérité du son dans l’air dans les conditions de l’expérience.
D’après la relation
d v t
, on peut écrire
321
5
8,5.10
c 3,4.10 m.s
T 2,5.10
C’est une vitesse qui correspond effectivement à celle connue théoriquement (
1
343m.s
à 20°C et
1
346m.s
à 25°C, sous une pression d’une atmosphère).