Semestre Rebondir Cours et exercices

Semestre Rebondir
Cours et exercices
D’après les notes de cours de Jean-Jacques Ruch,
Bruno Winckler et Samuel Le Fourn
Printemps 2013
Table des matières
1 Fonctions usuelles
1.1 Fonctions circulaires . . . . . . . . . . . . . . . . . .
1.1.1 Définitions . . . . . . . . . . . . . . . . . . .
1.1.2 Valeurs remarquables . . . . . . . . . . . . .
1.1.3 Angles associés . . . . . . . . . . . . . . . . .
1.1.4 Etude des fonctions sinus et cosinus . . . . .
1.1.5 Etude de la fonction tangente . . . . . . . . .
1.1.6 Exercices . . . . . . . . . . . . . . . . . . . .
1.2 Fonction logarithme . . . . . . . . . . . . . . . . . .
1.2.1 Définition de la fonction logarithme népérien
1.2.2 Propriétés de la fonction logarithme népérien
1.2.3 Etude de la fonction logarithme népérien . .
1.3 Fonction logarithme décimale . . . . . . . . . . . . .
1.4 Fonction exponentielle . . . . . . . . . . . . . . . . .
1.5 Croissances comparées . . . . . . . . . . . . . . . . .
1.6 Exercices . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
2
2
3
4
5
6
8
11
11
11
12
13
14
16
17
2 Primitives
2.1 Introduction . . . . . . . . . . . . . . . . .
2.2 Primitive d’une fonction sur un intervalle
2.2.1 Généralités . . . . . . . . . . . . .
2.2.2 Quelques primitives usuelles . . . .
2.2.3 Propriétés . . . . . . . . . . . . . .
2.3 Exercices . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
19
19
20
20
20
21
23
3 Intégrales
3.1 Définition de l’intégrale .
3.2 Intégrale et primitive . . .
3.3 Intégration par parties . .
3.4 Changement de variables
3.5 Exercices . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
24
24
26
27
28
30
4 Nombres complexes
4.1 Point de vue géométrique . . . . . . . . . . . . . . . .
4.2 Point de vue algébrique . . . . . . . . . . . . . . . . .
4.3 Exponentielle complexe . . . . . . . . . . . . . . . . .
4.4 Exercices . . . . . . . . . . . . . . . . . . . . . . . . .
4.4.1 Entraînement au calcul de nombres complexes
4.4.2 Exponentielle complexe et trigonométrie . . . .
4.4.3 Utilisation des complexes pour la géométrie 2D
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
32
32
34
36
39
39
39
40
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
Chapitre 1
Fonctions usuelles
1.1
1.1.1
Fonctions circulaires
Définitions
−→ −→
Soit C le cercle trigonométrique muni du repère orthonormé (O, OI, OJ). Pour θ un nombre réel
−→ −−→
quelconque, on considère le point M du cercle tel que θ soit la mesure en radians de l’angle (OI; OM ).
−→ −→
Définition 1. Dans le repère (O, OI, OJ), l’abscisse du point M est appelée cosinus de θ. On le note
cos θ. L’ordonnée du point M est appelée sinus de θ et est notée sin θ.
sin θ
. C’est aussi l’ordonnée du point
La tangente de θ (pour les réels θ tels que cos θ 6= 0) est le rapport
cos θ
T intersection de la droite (OM ) avec la tangente au cercle C en I, on la note tan θ.
T
y
J 1
M
tan θ
sin θ
cos θ
-1
O
N
1
I
x
-1
Remarques
D’après la définition ci-dessus on a pour tout réel θ
−1 6 cos θ 6 1
et
− 1 6 sin θ 6 1.
Rappelons que l’on a pour tout réel θ

 cos (x + 2kπ) = cos (θ)
sin (θ + 2kπ) = sin (θ)
∀k ∈ Z,

tan (θ + kπ) = tan (θ) si θ 6=
π
2
mod π
D’autre part si on considère le projeté N de M sur l’axe des abscisses alors on obtient un triangle rectangle
(ON M ) rectangle en N dont les côtés ont pour longueur |cos θ| et |sin θ|, et l’hypothénuse 1. Le théorème
de Pythagore entraîne alors la propriété fondamentale suivante :
∀θ ∈ R,
cos2 θ + sin2 θ = 1.
2
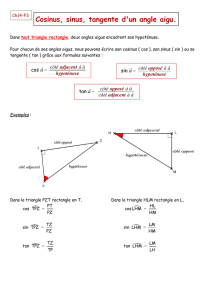
Si on utilise les formules classiques pour les angles d’un triangle rectangle on obtient :
coté adjacent
ON
\
cos N
OM =
=
= ON
hypothénuse
OM
1.1.2
coté opposé
NM
\
sin N
OM =
=
= N M.
hypothénuse
OM
Valeurs remarquables
Points cardinaux On remarque immédiatement
cos 0 = 1
cos π2 = 0
cos π = −1
sin π2 = 1
sin 0 = 0
sin π = 0
cos −π
2 =0
sin −π
2 = −1
Triangle rectangle isocèle
y
1
M
π
4
-1
O
1
x
N
-1
\
Soit ON M un triangle rectangle isocèle en N . Alors l’angle x = N
OM =
théorème de Pythagore on a
1 = OM 2 = ON 2 + N M 2 = 2ON 2 = 2 cos2
π
4.
De plus, d’après le
π
π
= 2N M 2 = 2 sin2 .
4
4
Le cosinus et le sinus étant ici positifs on en déduit : cos π4 = sin π4 =
√
2
2 .
Triangle équilatéral
y
1
M
π
6
-1
O
1
x
N
M’
-1
Soit ON M un triangle rectangle obtenu en coupant le triangle équilatéral OM M 0 en deux, suivant
\
la médiane (ON ) qui est aussi la médiatrice de [M M 0 ]. Alors l’angle x = N
OM = π6 , c’est la moitié de
3
0 OM qui est égal à π (le triangle OM M 0 étant équilatéral). D’après le théorème de Pythagore
\
l’angle M
3
on a
1
3
1
ON 2 = OM 2 − N M 2 = 1 − (M 0 M/2)2 = 1 − ⇒ ON 2 =
et N M 2 = .
4
4
4
√
Le cosinus et le sinus étant ici positifs on en déduit : cos π6 = 23 et sin π6 = 12 .
Si on construit maintenant un triangle équilatéral, comme sur le schéma ci-dessous, on obtient un angle
\
x=N
OM = π3 . Des calculs similaires à ceux qui précèdent nous donnent alors
π
1
cos =
3
2
√
π
3
sin =
.
3
2
et
y
1
M
π
3
-1
O
1
M’ x
N
-1
Nous pouvons donc faire le récapitulatif suivant :
1.1.3
π
6
π
4
√
√
x
0
cos x
1
3
2
sin x
0
1
2
tan x
0
√1
3
2
2
√
2
2
1
π
3
π
2
π
1
2
0
−1
1
0
non définie
0
√
3
2
√
3
Angles associés
Soient x un réel quelconque et M le point sur le cercle trigonométrique tel que x soit la mesure de l’angle
défini par l’axe des abscisses et (OM ). En effectuant des symétries du point M par rapport respectivement
à l’axe des abscisses, à l’axe des ordonnées et au point O, on obtient respectivement les points M1 , M2
et M3 , associés à des angles de mesure −θ, π − θ et π + θ. Si de plus on effectue une symétrie de M par
π
rapport à la droite y = x on obtient le point M4 associé à un angle de mesure − θ. Enfin, le symétrique
2
π
de M4 par rapport à l’axe des ordonnées définit un point M5 associé à un angle de mesure + θ.
2
4
y
M5
M4
M2
M
θ
x
M3
M1
En examinant les coordonnées de ces divers points, on peut établir les formules suivantes :

cos (−θ) 
sin (π/2 − θ) = cos (θ)

sin (π/2 + θ)
cos (π − θ)
= − cos (θ)
cos (π + θ)
sin (π − θ)
cos (π/2 − θ)
= sin (θ)

sin (−θ) 
sin (π + θ)
= − sin (θ)

cos (π/2 + θ)
D’autre part on peut en déduire les formules pour la tangente :
1.1.4
∀θ ∈ R, θ 6= π/2 + kπ, k ∈ Z
tan (θ + mπ) = tan (θ) m ∈ Z
tan (−θ) = − tan (θ)
∀θ ∈ R, θ 6= kπ/2, k ∈ Z
tan (π/2 − θ) = 1/ tan (θ)
tan (π/2 + θ) = −1/ tan (θ)
Etude des fonctions sinus et cosinus
Les deux fonctions cosinus et sinus sont définies sur R et sont bornées, car :−1 6 cos θ 6 1 et
−1 6 sin θ 6 1.
Pour tout réel θ on a cos (θ + 2π) = cos θ et sin θ + 2π = sin θ. On dit que les fonctions cosinus et sinus
sont périodiques de période 2π (ou « 2π-périodiques »). En conséquence, on peut réduire le domaine
d’étude à un intervalle de longueur 2π, par exemple [−π, π].
D’autre par comme pour tout réel θ, cos (−θ) = cos θ la fonction cosinus est paire, sa courbe
représentative dans un repère orthonormé est symétrique par rapport à l’axe des ordonnées ;
sin (−θ) = − sin θ la fonction sinus est impaire, sa courbe représentative dans un repère orthonormé
est symétrique par rapport à l’origine du repère. On peut donc réduire le domaine à l’intervalle
[0, π]. Les fonctions cosinus et sinus sont dérivables sur R et on a
cos0 (θ)
=
−sinθ
0
=
cos θ
sin (θ)
Une étude des variation et l’observation du cercle trigonométrique permet d’obtenir les tableaux de varia-
5
tions suivants :
θ
cos0 (θ)
0
0
1
−
π/2
−1
−
π
0
θ
sin0 (θ)
0
1
+
&
cos θ
0
%
sin θ
&
π/2
0
1
−
π
−1
&
0
0
−1
On en déduit les représentations graphiques suivantes.
1
-
cos θ
sin θ
-1
-
On peut encore donner les limites classiques suivantes :
lim
θ→0
1.1.5
sin θ
=1
θ
lim
θ→0
cos θ − 1
= 0.
θ
Etude de la fonction tangente
π
sin (θ)
+ kπ, k ∈ Z par tan (θ) =
.
2
cos (θ)
Pour tout réel θ on a cos (θ + π) = − cos θ et sin θ + π = − sin θ. Par conséquent la fonction tangente
est périodique de période π. On peut donc réduire le domaine d’étude à un intervalle de longueur π, par
−
exemple ] − π/2, π/2[. On complétera la représentation graphique par des translation de vecteur π →
x et
→
−
−π x .
D’autre part comme pour tout réel θ, cos (−θ) = cos θ et sin (−θ) = − sin θ, donc la fonction tangente est impaire : tan (−θ) = − tan θ. Sa courbe représentative dans un repère orthonormé est donc
symétrique par rapport à l’origine du repère. On peut donc réduire le domaine à l’intervalle [0, π/2[.
La fonction tangente est dérivable sur ] − π/2, π/2[ en tant que quotient de fonctions qui le sont, le dénominateur ne s’annulant pas. Si on pose u(θ) = sin (θ) et v(θ) = cos (θ), on a
La fonction tangente est définie pour tout θ ∈ R, θ 6=
tan0 (θ) =
u0 (θ)v(θ) − u(θ)v 0 (θ)
cos (θ) cos (θ) − sin (θ)(− sin (θ))
(cos (θ))2 + (sin (θ))2
=
=
.
(v(θ))2
(cos (θ))2
(cos (θ))2
Deux expressions sont possibles
tan0 (θ)
=
tan0 (θ)
=
(cos (θ))2 + (sin (θ))2
1
=
2
(cos (θ))
(cos (θ))2
2
2
(cos (θ))
(sin (θ))
+
= 1 + (tan (θ))2
2
(cos (θ))
(cos (θ))2
On en déduit que pour tout θ 6= π2 + kπ, k ∈ Z, la fonction dérivée est toujours strictement positive et
par conséquent que la fonction tangente est strictement croissante sur l’intervalle d’étude.
On peut déterminer facilement les limites aux bornes de l’intervalle. Comme on a
lim sin θ = 1
−
θ→ π
2
lim cos θ = 0+ ,
−
θ→ π
2
et
lim
+
θ→− π
2
lim cos θ = 0+ ,
sin θ = −1
−
θ→ π
2
6
on en déduit
lim tan θ = −∞
lim tan θ = +∞
−
θ→ π
2
−
θ→ π
2
On obtient le tableaux de variations suivant :
θ
tan0 (θ)
0
2
+
π/2
||
+∞
%
tan θ
0
On en déduit la représentation graphique suivante.
tan θ
7
1.1.6
Exercices
Exercice 1. Formules de somme et de différence
En remplaçant a et b par des valeurs particulières, complèter le tableau suivant avec les résultats donnés
ci-après :
cos (a + b) =
sin (a + b) =
cos (a − b) =
sin (a − b) =
{cos a cos b + sin a sin b, cos a sin b + sin a cos b, cos a cos b − sin a sin b, sin a cos b − cos a sin b}
Exercice 2. Formules de duplication
Déduire de l’exercice précédent les formules suivantes :

 cos2 a − sin2 a
2 cos2 a − 1
cos (2a) =
sin (2a) = 2 sin (a) cos (a)

1 − 2 sin2 a
et
tan (a + b) =
tan (a) + tan (b)
1 − tan a tan b
tan (a − b) =
tan (2a) =
2 tan a
1 − tan2 a
tan (a) − tan (b)
1 + tan a tan b
Exercice 3. A l’aide des formules de l’exercice 1 retrouver les formules suivantes :
Transformation de produit en somme

1

 cos a cos b = 2 (cos (a + b) + cos (a − b))
1
sin a sin b = 2 (cos (a − b) − cos (a + b))


sin a cos b = 12 (sin (a + b) + sin (a − b))
Transformation de somme en produit
cos p + cos q = 2 cos
cos p − cos q = −2 sin
p+q
2
p+q
2
p−q
2
cos
sin
p−q
2
sin p + sin q = 2 sin
p+q
2
cos
p−q
2
sin p − sin q = 2 sin
p−q
2
cos
p+q
2
Exercice 4. Montrer que si l’on pose t = tan (x/2) alors on a
cos x =
1 − t2
1 + t2
sin x =
2t
1 + t2
tan x =
2t
1 − t2
Exercice 5. Les dimensions du triangle OBM sont données sur la figure suivante :
M
1
O
1
3
B
Entourer parmi les données suivantes, celles qui sont correctes
√
2
2 2
\
OB =
sin BM
O = 31 OB =
3
3
2 2
1
\ =
\ =1
\ + cos BOM
\ =1
sin BOM
cos BOM
sin BOM
3
3
8
Exercice 6. Soit (C) un cercle de centre A et B un point de (C). 1. Construire les points D, E, F et G
du cercle (C) tels que :
−−→ −−→
3π −−→ −→
7π −−→ −→
3π
π −−→ −→
, (AB, AF ) =
, (AB, AG) = − .
(AB, AD) = , (AB, AE) =
3
4
6
4
−−→ −→
−→ −→
−→ −−→
−→ −→
2. Déterminer la mesure principale des angles (AD, AE), (AE, AG), (AG, AD) et (AG, AF ).
Exercice 7. Une tour est entouré par un large fossé comme le montre le dessin ci-dessous :
\
En se situant en A, l’angle M
AN vaut 42◦ . En reculant de 10 mètres (AB = 10) et en se positionnant en
◦
\
B l’angle M BN vaut 27 . Les triangles AM N et BM N sont rectangles en M .
1) En exprimant M N en fonction de AM de deux façons différentes (utiliser le fait que BM = BA+AM ),
calculer la longueur AM .
2) En déduire la hauteur de la tour.
Exercice 8. Exprimer, en fonction de R, le périmètre et l’aire de la figure :
R
2 rad
R
Exercice 9. Soient C et C 0 deux cercles de même centre O, de rayons respectifs R et R0 (R0 < R) et A et
B deux points de C. Pour aller de A à B deux chemins sont possibles :
trajet 1 : de A à B sur le cercle C
trajet 2 : de A à A0 , puis de A0 à B 0 sur C 0 , et enfin de B 0 à B comme le montre la figure ci-dessous :
C
B
C0
B’
O α
A’
A
1) On suppose que R = 150, R0 = 50 et α = 1 rad. Lequel des deux trajets est le plus court ?
2) On suppose que R = 300, R0 = 250 et α = 3 rad. Lequel des deux trajets est le plus court ?
3) Trouver une condition sur α pour que les deux trajets aient même longueur puis que le trajet 2 soit
plus long que le trajet 1.
Exercice 10. π/2 6 x 6 π
1) Sachant que
, et sans utiliser de calculatrice, donner une valeur exacte de cos x et de
sin x = 1/3
9
tan x.
p
√
2) Tout le monde sait bien que cos (π/8) = ( 2 + 2)/2. Déterminer sin (π/8).
Exercice 11. Simplifier l’expression
3π
+ x + sin −
−x
A(x) = cos (3π − x) + cos
2
2
π
Exercice 12.
1) Simplifier au maximun, pour tout réel t, l’expression (1 − cos t)(1 + cos t).
2) Démontrer que pour tout réel t : cos4 t − sin4 t = cos2 t − sin2 t.
Exercice 13. En remarquant que π/12 = π/3 − π/4, déterminer une valeur exacte de cos (π/12) puis de
cos (π/24).
Exercice 14. Résoudre dans R les équations et les inéquations suivantes :
√
π
1
π
2
= cos x +
b) sin (3x) =
c) cos 3x +
a) cos x =
2
2
4
3
√
2
1
d) cos (2x) = cos (3x)
e) cos (2x) ≤
f) sin (3x) >
2
2
Exercice 15.
1) Exprimer cos a cos b en fonction de cos (a + b) et cos (a − b).
2) En effectuant un changement de variable, démontrez que pour tous les nombres réels p et q, on a
p+q
p−q
cos
.
cos p + cos q = 2 cos
2
2
3) En déduire les solutions de l’équation cos x + cos (2x) + cos (3x) = 0.
1
Exercice 16.Soit f la fonction définie sur R par f (x) = −4x3 + 3x + .
2
1) Faire l’étude de la fonction (avec tableau de variations) et tracer sa courbe représentative.
2) Trouver les solutions dans [0; 2π] de l’équation, d’inconnue a, sin 3a = 1/2.
3) Montrer que pour tout réel a, sin 3a = 3 sin a − 4 sin3 a.
4) En déduire les solutions de l’équation f (x) = 0.
Exercice 17.
1) Sans faire l’étude de la fonction donner l’allure de la courbe de f (x) = sin (2x).
2) Faire l’étude de f , puis tracer sur un même graphique la courbe représentant f et celle de g(x) = sin x.
Exercice 18. Une
célèbre.
i limite
πh
→
− →
−
Soit x un réel de 0; . Dans le plan rapporté à un repère orthonormé direct (O; i ; j ), on considère les
2
points A(1, 0), M (cos x, sin x), P (cos x, 0) et T (1, tan x). Soient A1 l’aire du triangle OAM , A2 l’aire du
secteur de disque OAM et A3 l’aire du triangle OAT .
tan x
sin x
M
T
P
A
cos x
O
1) En comparant ces aires prouver que : sin x 6 x 6 tan x.
sin x
2) En déduire que cos x <
< 1.
x
sin x
(distinguer x > 0 et x < 0.)
3) Déterminer la limite en 0 de f (x) =
x
√
Exercice 19. Etudier la fonction f (x) = tan ( x).
Exercice 20. Un lapin désire traverser une route de 4 mètres de large. Un camion, occupant toute la
route, arrive à sa rencontre à une vitesse de 60 km/h. Le lapin décide au dernier moment de traverser, alors
10
que le camion n’est plus qu’à 7 mètres de lui. Son démarrage est foudroyant et on suppose qu’il effectue la
traversée en ligne droite à la vitesse de 30 km/h. Sur le schéma ci-dessous l’avant du camion est représenté
par le segment [CC 0 ]. Le lapin part du point A en direction de D. Cette direction est représentée par
\ avec 0 6 θ 6 π/2.
l’angle θ = BAD,
C’
4m
A
Camion
θ
7m
C
B
D
1) Déterminer les distances AD et CD en fonction de θ et les temps t1 et t2 mis par le lapin et le camion
pour parcourir respectivement AD et CD.
7
4
2) On pose f (θ) = + 2 tan θ −
. Montrer que le lapin aura traversé la route avant le passage du
2
cos θ
camion si et seulement si f (θ) > 0.
3) En utilisant la représentation graphique de f , donner un encadrement en degrés de l’angle selon lequel
doit partir le lapin pour ne pas être écrasé.
1.2
1.2.1
Fonction logarithme
Définition de la fonction logarithme népérien
Lorsque nous disposerons de la théorie de l’intégrale, nous démontrerons qu’il existe une unique fonction
f : ]0, +∞[→ R telle que f 0 (x) = 1/x pour tout x > 0 et f (1) = 0. En devançant un peu la théorie de
l’intégration, on a :
1
soit (C) la courbe représentative de la fonction x 7→ sur R∗+
x
y
Z
f (x2 ) =
1
x2
1
dt = −A2
t
Z
x1
f (x1 ) =
1
1
A2
x2
1
dt = −A1
t
(C)
A1
x1
1
x
Définition 21. Il existe une unique fonction f : ]0, +∞[→ R telle que f 0 (x) = 1/x pour tout x > 0 et
f (1) = 0. Cette fonction s’appelle la fonction logarithme népérien ou plus simplement logarithme. On
notera cette fonction par f (x) = ln (x)
1.2.2
Propriétés de la fonction logarithme népérien
Voici une première propriété qui est essentielle. Elle a permis de confectionner la règle à calcul, outil
largement utilisé par les ingénieurs ou les techniciens avant l’arrivée des calculatrices ou plus généralement
des ordinateurs.
Proposition 22. Pour tous réels a et b strictement positifs on a
ln (ab) = ln (a) + ln (b).
Démonstration : Soit a un réel strictement positif. Pour x > 0 on considère la fonction f (x) =
ln (ax). D’après la règle de dérivation des fonctions composées on a
f 0 (x) =
1
1
a = = (ln (x))0 .
ax
x
11
Par conséquent, la dérivée de la différence entre la fonction f et la fonction logarithme est nulle. C’està-dire que la différence entre ces deux fonctions est une constante k ∈ R. En particulier pour x = 1 on
a ln (a) = f (1) = k + ln (1) = k ; d’où ln (ax) = f (x) = ln (a) + ln (x). En remplaçant alors x par b on
obtient le résultat voulu.
Corollaire 23. Pour tous réels a et b strictement positifs on a
1
= − ln (a)
ln
a
a
= ln (a) − ln (b)
ln
b
√
1
ln ( a) = ln (a)
2
ln (an ) = n ln (a) pour tout n ∈ Z
Remarque
La dernière propriété se généralise à tous les réels. En effet, si a est un réel strictement positif et si α est
un réel quelconque :
ln (aα ) = α ln (a)
Démonstration : Ces résultats se déduisent assez facilement de la propriété de la proposition 2.
Soient a et b deux réels strictement positifs. On a
1
1
= ln
+ ln (a) − ln (a) = ln (1) − ln (a) = − ln (a)
ln
a
a
a
1
1
ln
= ln a
= ln (a) + ln
= ln (a) − ln (b)
b
b
b
√
√
√
√
√ √
1
ln (a) = ln ( a a) = ln ( a) + ln ( a) = 2 ln ( a) ⇒ ln ( a) = ln (a)
2
Pour le dernier point si n > 0 on montre le résultat par récurrence et pour n < 0 on applique ce résultat
à −n qui est positif. On obtient
1
ln (an ) = ln
= − ln (a−n ) = −(−n) ln (a) = n ln (a).
a−n
1.2.3
Etude de la fonction logarithme népérien
Proposition 24. La fonction logarithme népérien est une bijection continue, dérivable et strictement
croissante de ]0, +∞[ dans R. On a de plus :
lim ln (x) = −∞
x→0
lim ln (x) = +∞.
x→+∞
Démonstration : Dans la définition de la fonction logarithme il est dit que sa dérivée sur R∗+ est
f 0 (x) = 1/x. Comme cette fonction est strictement croissante continue (car dérivable) et dérivable. Pour
les limites on a : comme ln (2) > ln (1) = 0
ln (2n ) = n ln (2) → +∞
quand
n → +∞
Donc, la fonction logarithme n’est pas majorée. On en déduit lim ln (x) = +∞. Pour l’autre limite on
x→+∞
pose y = 1/x et on a
lim ln (x) = lim ln (1/y) = lim − ln (y) = −∞.
x→0
y→+∞
1/y→0
Le logarithme népérien est bien une bijection de ]0, +∞[ dans R.
12
Le tableau de variation de la fonction logarithme est donc
x
f 0 (x)
0
+∞
+
+∞
%
f (x)
−∞
Proposition 25. On a
ln (1 + x)
=1
x→0
x
lim
Démonstration : On a
ln (1 + x)
ln (1 + x) − ln (1 + 0)
= lim
x→0
x→0
x
x−0
lim
Comme la fonction logarithme est dérivable sur R+ et que 1 + x est positif si x > −1 et dérivable sur R
on en déduit que ln (1 + x) est dérivable sur ] − 1, +∞[, donc en particulier en x = 0. D’après la règle de
dérivation des fonctions composées, on obtient (ln (1 + x))0 = 1/(x + 1). La valeur de la limite que l’on
cherche est exactement la valeur de la dérivée calculée en x = 0, c’est-à-dire 1.
On obtient la représentation suivante. Comme la fonction logarithme est une bijection on peut tracer
sa fonction réciproque en prenant l’image par rapport à la droite y = x.
y
g(x) = exp(x)
f (x) = ln(x)
1
x
1
1.3
Fonction logarithme décimale
Comme on l’a remarqué la fonction logarithme népérien est particulièrement intéressante du fait de sa
propriété de transformation d’un produit en somme. Mais comme on utilise, pour écrire les nombres, le
système décimal, on lui préfère parfois une autre fonction possédant la même propriété de transformation
de produit en somme mais prenant la valeur 1 pour x = 10 (et donc 2 pour x = 100, 3 pour x = 1000,
etc...). Cette fonction sera appelée fonction logarithme décimal .
Définition 26. On appelle fonction logarithme décimal et on note log la fonction définie par :
log
:
]0, +∞[ →
R
x
7→ log (x) =
ln (x)
ln (10)
Par définition du logarithme décimal il est facile d’étudier les variations et de donner sa courbe repré-
13
sentative d’après celle du logarithme népérien. On a les propriétés suivantes :
Proposition 27. Soient a et b deux nombres strictement positifs
log (10n ) = n
pour n ≥ 0
log (ab) = log (a) + log (b)
1
= − log (a)
log
a
a
log
= log (a) − log (b)
b
√
1
log ( a) = log (a)
2
log (an ) = n log (a) pour tout n ∈ Z
y
f (x) = ln(x)
1
10
x
Remarque
Pour a > 0, on peut définir le logarithme de base a en posant pour x > 0
loga (x) =
1.4
ln (x)
ln (a)
Fonction exponentielle
Puisque la fonction logarithme népérien est une bijection de ]0, +∞[ dans R, nous savons que pour
tout nombre réel x, il existe un unique réel y, strictement positif, tel que ln (y) = x. Par définition, le
nombre y s’appelle exponentielle de x et est noté exp (x).
Définition 28. La fonction réciproque de la fonction logarithme népérien est la fonction exponentielle,
définie par :
exp : R →
R
x 7→ exp (x)
Elle vérifie
quelque soit le réel x > 0
exp (ln (x)) = x
quelque soit le réel x
ln (exp (x)) = x
Les propriétés de la fonction exponentielle se déduisent assez facilement de celles de la fonction logarithme.
Proposition 29. La fonction exponentielle définit une bijection continue et strictement croissante de R
dans ]0, +∞[. On a
lim exp (x) = 0
lim exp x = +∞.
x→−∞
x→+∞
De plus la fonction exponentielle est dérivable sur R et on a :
0
(exp (x)) = exp (x).
14
Démonstration : La fonction logarithme est une fonction continue strictement croissante de ]0, +∞[
dans R. Donc elle admet une fonction réciproque continue strictement croissante de R dans ]0, +∞[.
Comme on a lim ln (x) = −∞ et lim ln x = +∞ on en déduit que
x→+∞
x→0
lim exp (x) = 0
x→−∞
lim exp x = +∞.
x→+∞
Enfin la fonction logarithme est dérivable sur ]0, +∞[, de dérivée strictement positive 1/x. Par conséquent
sa fonction réciproque est dérivable sur R de dérivée :
0
(exp (x)) =
1
=
ln (exp (x))
0
1
1
exp (x)
= exp (x).
Voici d’autres propriétés qui se déduisent directement des propriétés analogues pour la fonction logarithme. 8
Proposition 30. Soient a et b deux réels
exp (a + b) = exp (a) exp (b)
1
exp (−a) =
exp (a)
exp (a)
exp (a − b) =
exp (b)
n
exp (n a) = (exp (a)) pour tout n ∈ Z
Remarque
La dernière propriété se généralise à tous les réels. En effet, si a et α sont deux réels quelconques :
exp (α a) = (exp (a))
α
Ceci permet d’écrire, pour tout réel x
exp (x) = ex
avec e = exp (1).
On obtient facilement le tracé de la fonction exponentielle à partir de celui de la fonction logarithme.
y
50
f (x) = exp(x)
40
30
20
10
-2
-1
0
1
2
3
4 x
Remarque
Pour a un réel strictement positif, il est possible de définir la fonction exponentielle de base a de R
dans R par
ax = exp (x ln (a)).
Attention, il ne faut pas confondre avec la fonction puissance qui pour un réel b fixé, associe à tout réel
strictement positif x la valeur xb = exp (b ln (x)).
15
1.5
Croissances comparées
Les limites calculées dans les propositions suivantes sont très souvent utilisées dans les exercices. Il
faut les connaitre pour les employer sans hésitation.
Proposition 31. On a
lim
x→+∞
ln (x)
=0
x
lim
x→+∞
exp (x)
= +∞.
x
Démonstration : L’étude de la fonction f (x) = x − 1 − ln (x) permet de montrer que pour
√ tout
ln ( x)
x ∈]0, +∞[, ln (x) ≤ x − 1 ≤ x. On en déduit que pour tout réel strictement positif x, on a √
≤1
x
et par conséquent
√
√
2
ln (x)
ln ( x)
ln ( x)
0≤
=2
=2 √ 2 ≤ √
x
x
( x)
x
Puisque ce dernier terme tend vers 0 lorsque x → +∞, cet encadrement nous donne la première limite.
Pour la seconde, comme y = exp (x) → +∞ quand x → +∞, on a
lim
x→+∞
exp (x)
exp (x)
y
= lim
= lim
= +∞
x→+∞ ln (exp (x))
y→+∞ ln (y)
x
d’après la limite précédente (y et ln (y) sont positifs).
Proposition 32. Soient a et b deux réels tels que a > 1 et b > 0. On a
ln (x)
=0
xb
et
ax
= +∞
x→+∞ xb
et
lim
x→+∞
lim
lim xb ln (x) = 0
x→0
lim xn ax = 0
x→−∞
pour tout entier n ∈ N
Démonstration : Soit b > 0. Pour tout réel x > 0 on a ln (x) =
xb → +∞ quand x → +∞. D’où on obtient :
1
ln (xb ). Puisque b > 0, on a
b
ln (x)
1 ln (xb )
= lim
=0
b
x→+∞ x
x→+∞ b
xb
lim
d’après la première proposition ci-dessus. De même manière on a :
1 ln (1/x)b
b
lim x ln (x) = lim −
=0
x→0
x→0
b (1/x)b
d’après la première proposition et car (1/x)b → +∞ quand x → 0.
Pour la prochaine limite on fait la transformation suivante, comme a > 1 et b > 0 :
ax
exp (ln (ax ))
exp (x ln (a))
ln (x)
lim
=
lim
=
lim
=
lim
exp
x
ln
(a)
−
b
.
x→+∞ exp (ln (xb ))
x→+∞ exp (b ln (x))
x→+∞
x→+∞ xb
x
Or on sait que ln (x)/x → 0 quand x → +∞, donc le terme entre crochets converge vers ln (a). Comme
a > 1, ln (a) > 0 et donc on obtient le résultat.
Pour la dernière limite il faut faire attention à ce que l’on fait car x est négatif, on ne peut donc pas
prendre le logarithme de x ! Mais en fait ce n’est pas nécessaire. En effet :
lim xn ax = lim (−1)n
x→−∞
x→−∞
d’après la limite précédente car −x → +∞.
(−x)n
=0
a−x
16
1.6
Exercices
Exercice 1. Résoudre les équations
ln (x) = 4
ln (x) = −2
3 ln (x) = 2
ln (2x) + ln (5) − π = 0
Exercice 2. Ecrire plus simplement
ln (14) − ln (7);
ln (8) − ln (12) + ln (15);
5
2
ln
+ ln
2
5
;
ln (10000) − ln (0.01);
ln (100)
;
ln (10)
√
√
ln (3 + 2 2) + ln (3 − 2 2)
Exercice 3. Démontrer que pour tout x réel, on a : ln (1 + ex ) = x + ln (1 + e−x ).
Exercice 4. Résoudre dans R les équations :
ln (x) + ln (x − 1) = ln (2) + ln (3);
ln (x) + ln (4 − x) = ln (2x − 1) + ln (3)
Exercice 5. Résoudre dans R les équations :
ln (x2 + x) = 1
x+1
ln
= −1
x−1
ln (x) + ln (x + 1) = 1
ln (x + 1) = −1 + ln (1 − x)
Exercice 6. Résoudre les inéquations suivantes :
ln (x) < 1
2 ln (x) − 1 ≥ 0
ln (x) > ln (2x − 1)
ln (1 + ex ) > 0
ln (2x − 1) + 1 ≤ 0
1 + ex
≥1
ln
1 − ex
Exercice 7. Montrer que pour tout réel x > 0, ln (1 + x2 ) > x −
x2
2
Exercice 8. Déterminer les limites suivantes :
lim ln (1 +
x→+∞
p
1 + x2 );
lim
x→0
ln (x)
;
x
lim x +
x→0
1 ln (x)
+
.
x
x2
Exercice 9. Faire l’étude et la représentation graphique des fonctions suivantes :
1 + ln (x)
2+x
f1 (x) =
f2 (x) = ln (x) − 3(ln (x))2
f3 (x) = ln
.
x
2−x
Exercice 10. Ecrire plus simplement les expressions suivantes :
e2x e1−2x ;
e2x+3
;
ex−1
(ex + e−x )2 ;
e−2x −
e2x + 1
.
e2x
Exercice 11. Montrer que pour tout x ∈ R,
exp (x) ≥ x + 1.
Exercice 12. Résoudre dans R les inéquations suivantes :
exp (2x) − 1 > 0;
exp (x) + 3
> 2;
exp (x) + 1
exp (x) − exp (2x) ≤ 0;
17
exp (2x + 5) < exp (1 − x)
Exercice 13. Déterminer les limites suivantes :
2
a) lim ex
2
−3x−5
b) lim ex
x→+∞
−3x−5
c) lim 2 + 3e−x
x→−∞
e) lim 3xe−x
2ex − 5
x→+∞
3x
h) lim
f) lim (x + 1)ex
x→+∞
x→−∞
ex + e−x
x→−∞ 3 + ex
ex − 1
x→0
x3
g) lim
+1
x→+∞
ex + 1
x→+∞ e2x
d) lim
2
i) lim
Exercice 14. Résoudre dans R les équations suivantes :
e(2x+1) − 1 = 0;
ex+1 − e2x−3 = 0;
ex−1 e3x+5 = 1;
2ex + 1
= 2e3 + e−x .
ex
e2x + ex − 2 = 0;
Exercice 15. Déterminer les limites suivantes :
1. lim+
x→0
x+2
ln (x)
2. lim+ 2x ln (x +
x2
√
x)
x3 − 2x2 + 3
x→+∞
x ln (x)
3. lim
x→0
√
e x+1
4. lim
x→+∞ x + 2
5. lim+
x→0
2
ln
7. lim
x→−∞ x + 1
10. lim
x→0+
x3 + 4
1 − x2
x(xx − 1)
ln (x + 1)
ln (x)
13. lim (1 + x)
16. lim
x→+∞
ex + 1
x+2
(x + 1)x
x→+∞ xx+1
19. lim
6. lim+
x→0
xx − 1
ln (x + 1)
8. lim+ (x − 2)2 ln (x3 − 8)
9.
11. lim x ln (x) − x ln (x + 2)
12. lim
x→2
lim
x→(−1)+
(x2 − 1) ln (7x3 + 4x2 + 3)
2
x→+∞
14. lim
x→+∞
x→0+
ln (3x + 1)
2x
x+1
x−3
ex − ex
x→+∞ x2 − x
x
15. lim
x→+∞
1
x+1
x3 + 5
x2 + 2
x−1
1
17. lim (ln (1 + x)) ln (x)
x→0+
p
x ln (x2 + 1)
x→+∞
1 + ex−3
20. lim
18
x(x )
x
x→+∞ x(x )
18. lim
x+1
x2 +1
Chapitre 2
Primitives
2.1
Introduction
On considère la fonction affine f définie par f (x) = 2x + 1.
Soit D la droite représentant f dans un repère orthonormal, soient A et B deux points de D et soient
A0 et B 0 les projetés de A et B sur l’axe Ox parrallèlement à Oy.
10
D
y
B’
8
6
A’
4
A
2
-5
-4
-3
-2
1 A’ 2
-1
3 B’ 4
5 x
-2
-4
-6
-8
-10
On suppose que les abscisses respectives de de A et B sont x1 et x2 avec x1 < x2 , f (x1 ) > 0 et
f (x2 ) > 0 comme sur le graphique ci-dessus. L’aire du trapèze rectangle ABB 0 A0 est donnée par :
A=
AA0 + BB 0 0 0
AB
2
Comme A et B sont sur la droite D leurs ordonnées respectives sont f (x1 ) = 2x1 + 1 et f (x2 ) = 2x2 + 1.
On a donc : AA0 = f (x1 ), BB 0 = f (x2 ) et A0 B 0 = x2 − x1 . Par conséquent on obtient :
=
f (x1 ) + f (x2 )
2x1 + 1 + 2x2 + 1
(x2 − x1 ) =
(x2 − x1 )
2
2
(x1 + x2 + 1)(x2 − x1 ) = x22 + x2 − x21 − x1
=
x22 + x2 − (x21 + x1 )
A =
On appelle g la fonction définie par g(x) = x2 + x, on peut donc écrire A = g(x2 ) − g(x1 ).
On peut remarquer que g est une fonction dérivable sur R et que pour tout x ∈ R, on a g 0 (x) = 2x + 1 =
f (x). La fonction g est donc une fonction dont la dérivée est f . On dit que g est une primitive de f .
19
2.2
Primitive d’une fonction sur un intervalle
2.2.1
Généralités
Définition 1. Soit f une fonction définie sur un intervalle I. On appelle primitive de f sur I, toute
fonction F définie et dérivable sur I, dont la dérivée est f .
Exemple
Une primitive de la fonction f définie sur R par f (x) = 2x, est la fonction F définie sur R par F (x) = x2 .
En effet F est dérivable sur R et on a pour tout x ∈ R, F 0 (x) = 2x = f (x).
On peut remarquer qu’on aurait pu choisir pour F , F (x) = x2 + 1 ou F (x) = x2 − π ou plus généralement,
si k est une constante réelle, F (x) = x2 + k.
Une fonction n’a pas une seule primitive.
Théorème 2.
Si F0 est une primitive de f sur I, alors l’ensemble des primitives de f sur I est l’ensemble
des fonctions de la forme, pour tout x ∈ I, F (x) = F0 (x) + k, avec k ∈ R. Autrement dit, deux
primitives d’une même fonction diffèrent d’une constante.
Démonstration : Soit F une primitive de f sur I et k une constante réelle. Si G = F + k alors G est
dérivable sur I en tant que somme de deux fonctions dérivables sur I. Comme la dérivée d’une constante
est nulle, on a G0 = F 0 = f . La fonction G est donc une primitive de f sur I.
L’ensemble des fonctions F + k, avec k ∈ R, est donc contenue dans l’ensemble des primitives de f sur I.
Réciproquement si G est une primitive de f sur I, alors G est dérivable sur I et on a G0 = f . Comme on
sait que F est une primitive de f sur I, on a aussi F 0 = f . On en déduit que G0 = F 0 , donc G0 − F 0 = 0
c’est-à-dire (G − F )0 = 0. La dérivée de la fonction G − F est nulle sur I, donc G − F est constante.
C’est-à-dire G − F = k, k ∈ R, ou encore G = F + k avec k ∈ R.
L’ensemble des primitives de f sur I est donc contenu dans l’ensemble des fonctions G = F + k, avec
k ∈ R. D’où on en déduit le résultat.
Corollaire 3. Soit f une fonction admettant des primitives sur un intervalle I et soit x0 ∈ I et y0 ∈ R.
Il existe une et une seule primitive F de f sur [a, b] telle que F (x0 ) = y0 .
Démonstration : Soit F0 une primitive de f sur I. Si F est une autre primitive de f sur I, on a
pour tout x dans I, F (x) = F0 (x) + k. On veut que F (x0 ) = y0 pour un certain x0 ∈ I. On en déduit que
F0 (x0 ) + k = y0 , c’est-à-dire k = y0 − F (x0 ). L’application F (x) = F0 (x) − F0 (x0 ) + y0 est une primitive
de f sur I qui vérifie le résultat, de plus elle est unique par construction.
Le théorème suivant est admis.
Théorème 4.
Toute fonction continue sur un intervalle I a des primitives sur I.
Remarque
Certaines fonctions non continues peuvent aussi avoir des primitives.
2.2.2
Quelques primitives usuelles
Z
Soit f : I → R continue. On notera
f (x)dx = F (x) + C où F est une primitive de f . Si f n’est pas
définie sur I on prend le plus grand sous-intervalle sur lequel elle est définie. La formule peut-être vraie sur
Z b
plusieurs intervalles, mais la relation
f (t)dt = F (b) − F (a) ne peut-être utilisée que sur un intervalle
où f est définie.
a
20
Fonction
Primitives
Z
1
x
Z
xα , α 6= −1
1
dx = ln |x| + C
x
xα dx =
xα+1
+C
α+1
Z
exp (x)dx = exp (x) + C
exp (x)
Z
exp (mx), m 6= 0
exp (mx)dx =
1
exp (mx) + C
m
Z
cos (x)dx = sin (x) + C
cos (x)
Z
sin (x)dx = − cos (x) + C
sin (x)
Z
tan (x)
1
cos2
(x)
= 1 + tan2 (x)
tan (x)dx = − ln | cos (x)| + C
Z
1
cos2
(x)
dx = tan (x) + C
Ces primitives ont été obtenues à partir des dérivées classiques.
2.2.3
Propriétés
Proposition 5. Soit I un intervalle de R.
Si F est une primitive de f sur I et G une primitive de g sur I alors F + G est une primitive de f + g
sur I. Si F est une primitive de f sur I et a un réel alors aF est une primitive de af sur I.
Remarque
Ces résultats se déduisent directement des résultats similaires pour la dérivation. Attention, une primitive
d’un produit ne sera pas obtenu en prenant le produit des primitives, puisque la dérivée d’un produit n’est
pas le produit des dérivées.
Proposition 6. Soit u une fonction dérivable.
• Une fonction de la forme u0 un avec n ∈ Z/−1 a pour primitives les fonctions de la forme
avec C ∈ R.
1
un+1 + C
n+1
u0
• Une fonction de la forme
a pour primitives les fonctions de la forme ln |u| + C avec C ∈ R sur tout
u
intervalle ou la fonction u ne s’annule pas.
√
u0
• Une fonction de la forme √ a pour primitives les fonctions de la forme 2 u + C avec C ∈ R sur tout
u
intervalle ou la fonction u est strictement positif.
• Une fonction de la forme u0 exp (u) a pour primitives les fonctions de la forme exp (u) + C avec C ∈ R.
Démonstration : On ne démontre que le premier résultat. Les autres qui se retrouvent par des
méthodes identiques sont laissées au lecteur.
21
La formule de dérivation des fonctions composées permet de calculer la dérivée de un+1 lorsque n est un
entier relatif différent de −1. On a (un+1 )0 = (n + 1)u0 un . Donc un+1 est une primitive de (n + 1)u0 un .
1
1
1
est une constante,
un+1 est une primitive de
(n + 1)u0 un = u0 un .
Comme
n+1
n+1
n+1
22
2.3
Exercices
Exercice 1. On note f une fonction définie sur R. Trouver dans chacun des cas suivants une primitive de
f.
a) f (x) = 2
b) f (x) = x
c) f (x) = 5x
d) f (x) = −4x2
e) f (x) = x2 − 3x + 2
Exercice 2. Pour chacune des fonctions f donner l’ensemble des primitives de f sur l’intervalle I.
a) f (x) = 3x2 + 2x + 1
b) f (x) = −x2 + 1
c) f (x) = x1
d) f (x) = exp (x)
I
I
I
I
=R
=R
=]0, +∞[
=R
1
Exercice 3. Soit f définie sur I =]0, +∞[ par f (x) = x − 2 . Déterminer les primitives de f sur I.
x
Existe-t-il une primitive de f prenant la valeur 2 pour x = 1 ?
Exercice 4. Pour chacune des fonctions f ci-dessous, donner un intervalle I sur lequel f a des primitives
et donner toutes les primitives de f sur cet intervalle.
x4 + 1
1
c) f (x) =
a) f (x) = x7
b) f (x) = 3
x
x2
Exercice 5. Pour chacune des fonctions f ci-dessous, donner un intervalle I sur lequel f a des primitives
et donner toutes les primitives de f sur cet intervalle.
2
exp (x) + 4
a) f (x) = 5x2 + x +
b) f (x) = 3 sin (x) + 2 cos (x)
c) f (x) =
x
3
Exercice 6. Donner une primitive de la fonction f en précisant sur quel intervalle elle est définie.
a) f (x) = 2(2x + 1)3
b) f (x) = (3x + 1)−5
c) f (x) = (−2x + 1)5
d) f (x) =
2x + 1
x2 + x + 1
e) f (x) = sin (x) cos3 (x) f ) f (x) =
g) f (x) =
2x
x2 + 1
h) f (x) =
1
2x + 1
j) f (x) = x exp (x)
k) f (x) = exp (3x + 1)
1
m) f (x) = √
x+1
3x
n) f (x) = 2
x +1
23
1
(ln x)2
x
x+2
x2 + 4x + 3
1
1
l) f (x) = 2 exp
x
x
i) f (x) =
1
o) f (x) = 2
x
r
1+
1
x
Chapitre 3
Intégrales
3.1
Définition de l’intégrale
Définition 1. Soit f une fonction continue et positive sur un intervalle [a, b]. Soit (C) sa courbe repréZ b
sentative dans un repère orthogonal. On appelle intégrale de a à b de la fonction f , et on note
f (t)dt,
a
le réel mesurant l’aire, en unités d’aires, de la partie du plan limitée par la courbe (C), l’axe (Ox) et les
droites x = a et x = b c’est-à-dire l’ensemble des points M (x, y) tels que
a≤x≤b
0 ≤ y ≤ f (x)
y
4
(C)
2
Z
b
f (t) dt
a
−2
2
x
4
a
6
b
8
−2
Z
Exemple : Si f est une fonction constante positive k alors
Z b
On a
k dt = k(b − a).
b
f (t) dt correspond à l’aire d’un rectangle.
a
a
Proposition 2. Soit f une fonction continue et positive sur un intervalle I. Alors pour tous réels a, b et
c dans l’intervalle I on a
Z b
Z c
Z b
f (t) dt =
f (t) dt +
f (t) dt.
a
a
c
Cette relation est appelée relation de Chasles pour l’intégrale.
Remarque
Si c appartient à l’intervalle [a, b] ce résultat se comprend bien, comme on peut le voir sur le graphique
ci-dessous :
24
(C)
a
b
Z
c
Z
a
b
b
Z
f (t) dt =
On a
c
f (t) dt +
f (t) dt. On en déduit que :
a
c
c
Z
Z
Z
f (t) dt −
f (t) dt =
a
b
a
b
f (t) dt.
c
Pour que la relation de Chasles reste vraie quelque soit l’ordre des réels a, b et c on adopte la convention :
Z
−
b
Z
f (t) dt =
c
Z
b
Z
f (t) dt =
On a alors
a
c
c
f (t) dt.
b
b
Z
f (t) dt +
f (t) dt pour tous les reéls a, b et c dans un intervalle I sur lequel
a
c
f est continue et positive.
Pour l’instant nous n’avons travaillé qu’avec des fonctions qui sont toujours positives. Mais que se
passe-t-il pour les fonctions négatives ou pour celles qui changent de signe ?
Définition 3. Soit f une fonction continue et négative sur un intervalle [a, b]. Soit (C) sa courbe repréZ b
sentative dans un repère orthogonal. On appelle intégrale de a à b de la fonction f , et on note
f (t) dt,
a
l’opposé du nombre réel mesurant l’aire, en unités d’aires, de la partie du plan limitée par la courbe (C),
l’axe (Ox) et les droites x = a et x = b.
a
b
Z
b
f (t) dt = −A
a
(C)
Par extension on peut donc définir l’intégrale d’une fonction continue qui change de signe.
Définition 4. Soit f une fonction continue (qui peut changer de signe) sur un intervalle [a, b]. Soit (C)
sa courbe représentative dans un repère orthogonal. On appelle intégrale de a à b de la fonction f , et on
Z b
note
f (t) dt, la différence entre l’aire obtenue lorsque f est positive et le nombre correspondant à l’aire
a
obtenue lorsque f est négative.
25
(C)
A1
A3
a
b
A2
A4
b
Z
f (t) dt = A1 − A2 + A3 − A4
a
Remarque
La relation de Chasles pour l’intégrale reste vraie pour une fonction continue sur un intervalle, négative
ou qui change de signe.
3.2
Intégrale et primitive
Le résultat suivant, que l’on admet, est essentiel en analyse.
Théorème 5.
Soit f une fonction continue sur un intervalle I. Si a ∈ I alors la fonction F : I → R définie
par :
Z x
∀x ∈ I, F (x) =
f (t) dt
a
est l’unique primitive de f qui s’annule en a.
Remarque
Z
a
f (t) dt = F (a) = 0.
Cela signifie en particulier que :
a
Corollaire 6. Si f est une fonction continue sur un intervalle I, alors pour tous réels a et b de I on a :
Z
b
f (t) dt = F (b) − F (a)
a
où F est une primitive quelconque de F sur I.
Remarque
Z
On note aussi
b
f (t) dt = [F (t)]ba = F (b) − F (a).
a
Z
Démonstration : D’après le théorème 5, si a ∈ I, x 7→ G(x) =
x
f (t) dt est l’unique primitive de
a
f sur I qui s’annule en a. Soit F une primitive de f sur I, on a donc F (x) = G(x) + C ou C est une
constante réelle. Donc on obtient :
Z b
F (b) − F (a) = G(b) + C − G(a) − C = G(b) =
f (t) dt
a
car G s’annulle en a.
Dans la proposition suivante nous regroupons différentes propriétés. Certaines ont déjà été vues.
Proposition 7. Soit f et g deux fonctions continues sur un intervalle I ; a, b et c étant trois éléments de
26
I et λ un réel, on a :
Z
a
f (t) dt = 0
(1)
a
Z
a
b
Z
f (t) dt = −
f (t) dt
b
Z
b
c
f (t) dt =
a
Z
b
Z
f (t) dt +
f (t) dt
a
b
Z
b
Z
Z
λf (t) dt = λ
a
b
g(t) dt
f (t) dt +
(4)
a
a
a
b
(3)
c
(f (t) + g(t)) dt =
Z
(2)
a
Z
b
f (t) dt
(5)
a
Z
b
f (t) dt ≥ 0
si f ≥ 0 sur [a, b] alors
(6)
a
Z
b
Z
si f ≥ g sur [a, b] alors
f (t) dt ≥
a
Z
Z
b
b
|f (t)| dt
f (t) dt ≤
a
a
b
g(t) dt
(7)
a
(8)
Démonstration : Les trois premières propriétés ont déjà été démontrées.
Pour la quatrième, on note F une primitive de f sur I et G une primitive de g sur I. Alors on sait que
F + G est une primitive de f + g sur I. On a alors :
Z b
Z b
Z b
(f + g)(t) dt = (F + G)(b) − (F + G)(a) = F (b) − F (a) + G(b) − G(a) =
f (t) dt +
g(t) dt.
a
a
a
La cinquième propriété se démontre de la même manière.
Pour la propriété suivante cela provient de la définition de l’intégrale d’une fonction continue et positive,
qui est égale à une aire donc un réel positif.
La septième propriété se déduit directement de celle que l’on vient de démontrer en appliquant le résultat
Z b
à la fonction f − g. En effet, si f ≥ g alors f − g ≥ 0 et et donc on a
(f − g)(t) dt ≥ 0. On en déduit
a
le résultat en utilisant la propriété (4).
Il ne reste plus qu’à démontrer la dernière propriété. Rappelons d’abord que si A est un nombre réel on a
−|A| ≤ A ≤ |A|. En appliquant ceci à la fonction f on obtient pour tout t ∈ I :
−|f (t)| ≤ f (t) ≤ −|f (t)|
Comme la fonction valeur absolue est continue, la composée de la fonction f et de la fonction | | est une foncZ b
Z b
Z b
tion continue sur I on peut donc calculer son intégrale. Par conséquent on a −
|f (t)| dt ≤
f (t) dt ≤
|f (t)| dt
a
c’est-à-dire
a
a
Z
Z
b
b
f (t) dt ≤
|f (t)| dt.
a
a
3.3
Intégration par parties
Théorème 8.
Soient f et g deux fonctions dérivables sur un intervalle I dont les dérivées sont continues sur
I. Soient a et b deux éléments de I. On a
Z b
Z b
f (t)g 0 (t) dt = [f (t)g(t)]ba −
f (t)g 0 (t) dt.
a
a
27
Démonstration : Soient f et g deux fonctions dérivables sur un intervalle I, dont les dérivées f 0 et
g sont continues sur I. La formule de dérivation d’un produit, permet d’écrire pour tout t ∈ I
0
(f (t)g(t))0 = f 0 (t)g(t) + f (t)g 0 (t).
Les fonctions étant continues on a pour a ∈ I et b ∈ I :
Z
b
f (t)g 0 (t) dt
b
Z
(f (t)g(t))0 dt −
=
a
a
=
Z
b
f (t)g 0 (t) dt,
a
Z
[f (t)g(t)]ba −
b
f (t)g 0 (t) dt.
a
Remarque
Après avoir fait une intégration par parties, la nouvelle intégrale que l’on à calculer doit être plus simple
que la première. Si ce n’est pas le cas, il faut peut-être modifier le choix de f et g 0 .
On pourra si besoin est, utiliser plusieurs fois l’intégration par parties.
Z π2
x cos (x) dx. On pose f (x) = x et g 0 (x) = cos (x). On
Exemple : On souhaite calculer l’intégrale
0
a alors f 0 (x) = 1 et g(x) = sin (x). Les fonctions f et g sont dérivables et leurs dérivées sont continues sur
[0, π/2]. On a par conséquent :
Z
π
2
[x sin (x)]0 −
x cos (x) dx =
sin (x) dx =
0
0
π
π
π
sin ( ) − [− cos (x)]02
2
2
π
−1
2
=
3.4
π
2
Z
π
2
Changement de variables
Théorème 9.
Soit f une fonction continue sur un intervalle I de R. Soit u une fonction dérivable à valeurs
dans I et de dérivée continue sur [a, b]. Alors on a :
Z
b
Z
0
u(b)
f (u(x))u (x) dx =
a
f (x) dx.
u(a)
Remarque
Z
En pratique il arrive souvent que l’on doive effectuer le changement de variable v dans
b
f (t) dt. On
Ra
commence en général par faire le changement de variable v dans la calcul de la primitive
f (t) dt. Pour
R
ce faire on effectue les transformations successivement sur chacun des composants de f (t) dt. A cet effet,
on écrit la table du changement de variable, où chaque symbole de la première colonne est remplacé par
le symbole de la deuxième colonne. On note u la fonction réciproque de v ( c’est-à-dire u(v(x)) = x).
R
t
u(t)
dt
u0 (t) dt
f (t)
f (u(t))
f (t) dt
R
f (u(t))u0 (t) dt
28
R
On calcule ensuite la primitive G égale à f (u(t))u0 (t) dt et une primitive de f est alors donnée par
G(v(x)).
Il est évident qu’un changement de variable doit amener à un calcul de primitive plus simple que le
calcul initial, sinon il faut faire un autre choix de changement de variable !
29
3.5
Exercices
1
Exercice 1. On considère la fonction f définie sur R par f (x) = x + 2.
2
Z 4
1) Représenter graphiquement f . Calculer l’intégrale
f (t) dt sans chercher une primitive de f .
−2
Z 4
f (t) dt = F (4) − F (−2)
2) Déterminer une primitive F de f sur R et vérifier que
−2
Exercice 2. Calculer chacune des intégrales suivantes :
Z 3
Z 1
Z
a)
(t + 4) dt
b)
(2t2 − 1) dt
c)
−1
0
Z
0
(4x − x ) dx
e)
1
−1
Z
2
Z
3
(3x ) dx
f)
4
2
1
g)
2
2
Z
1
√ dt
t
π
sin (x) dx
d)
0
Z
1
dt
t6
h)
0
√
2
x
x2
+1
dx
1
2
x
Exercice 3. Soit n un entier naturel non nul. On pose un =
exp −
dx.
n
0
1) En déterminant un encadrement de la fonction intégrée, donner un encadrement de un .
2) Montrer que la suite (un ) est monotone.
3) En déduire que la suite (un ) est convergente et déterminer sa limite.
Z
Exercice 4. Exprimer le produit cos (x) cos (3x) cos (5x) comme une somme au moyen de sin (9x), sin (7x),
Z π/2
sin (3x) et sin (x). En déduire
cos (x) cos (3x) cos (5x) dx.
0
Exercice 5. Soit f une fonction continue
sur un Zintervalle [−a, a] avec a > 0.
Z a
a
1 Montrer que si f est paire on a
f (t) dt = 2
f (t) dt.
−a
0
Z a
2 Montrer que si f est impaire on a
f (t) dt = 0.
−a
Z
π/3
Exercice 6. Soient n ∈ Z, Fn =
Z
n
π/6
n
π/3
(sin (t)) cos (t) dt et Gn =
n
5
(sin (t)) (cos (t)) dt.
π/6
1) Montrer que (sin (t)) cos (t) est de la forme u(x)u0 (x) pour une fonction u convenable. En déduire Fn .
n
4
n
n+2
n+4
2) Montrer que (sin (t)) (cos (t)) = (sin (t)) − 2 (sin (t))
+ (sin (t))
.Calculer Gn .
3
0
3) Montrer que (cos (t)) est de la forme (1 − u(x))u (x) pour une fonction u convenable. En déduire
Z π/3
3
Gn =
(cos (t)) dt.
π/6
Exercice 7. En effectuant une intégration par parties, calculer chacune des intégrales suivantes :
Z π
Z 2
Z 1
a)
x sin (x) dx
b)
x ln (x) dx
c)
(2x + 1) exp (x) dx
1
0
Z x
Z x
Z0 e
ln (x)
e)
ln (t) dt (x > 0) f)
(x3 + 1) ln (x) dx
d)
x2
1
1
1
Z
3
ln (x)
dx.
xn
2
Z π4
Z π4
2
Exercice 9. On pose I =
(2x + 1) cos (x) dx et J =
(2x + 1) sin2 (x) dx.
Exercice 8. Soit n ∈ N, calculer l’intégrale suivante :
0
0
1) Calculer I + J (sans calculer I et J).
2) Calculer I − J à l’aide d’une intégration par parties.
3) En déduire les valeurs de I et J.
Exercice 10. En effectuant deux intégrations par parties, calculer chacune des intégrales suivantes :
Z 1
Z 0
Z π
a)
(x + 1)2 exp (−x) dx
b)
x2 sin (2x) dx
c)
exp (2x) sin x dx
Z−1
Z −π
Z 0x
x
e
ln (x)
e)
ln (t) dt (x > 0)
f)
(x3 + 1) ln (x) dx
d)
x2
1
1
1
30
Exercice 11. En posant le changement de variable u =
ln (2)
Z
0
p
exp (x) − 1 montrer que
p
π
exp (x) − 1 dx = 2 − .
2
Exercice 12. Calculer les intégrales suivantes en faisant le changement de variable indiqué
√
a)
R3
,
u(x) =
b)
R2
,
u(t) = exp (t)
c)
R8
,
u(x) =
√dx
2 x x+1
dt
1 exp (t)−exp (−t)
5
√
ln ( 3 x − 1
Z
Exercice 13. Calculer l’intégrale I =
1
1+x
√
3
x
p
1 − x2 dx en effectuant le changement de variable qui consiste
1
à remplacer x par cos (t) (on fera attention à bien définir l’intervalle de variation de t de manière à avoir
un changement de variable bijectif).
31
Chapitre 4
Nombres complexes
Dans ce chapitre, nous présenterons les complexes des deux façons qui permettent de les appréhender.
Les nombres complexes furent d’abord introduits sous forme algébrique, mais c’est le point de vue géométrique de Gauss qui a convaincu de leur intérêt. C’est ce point de vue que nous présenterons dans un
premier temps.
4.1
Point de vue géométrique
Définition 1. Soit un repère orthonormé (O, Ox, Oy). Un nombre complexe est un nombre de la forme
x + iy, où x et y sont des réels. À chaque point du plan M de coordonnées (x, y), qui sont aussi les
−−→
coordonnées du vecteur OM , on associe le nombre complexe x + iy, et on dit alors que x + iy est l’affixe
de M .
Remarque
Les nombres réels font partie des nombres complexes, ce sont ceux qui s’écrivent x + i0. Ils correspondent
géométriquement aux points de l’axe des abscisses. Les nombres sur l’axe des ordonnées sont appelés
nombres imaginaires purs et s’écrivent sous la forme iy.
Un vocabulaire propre aux nombres complexes, et correspondant à chaque notion géométrique de base,
est présenté dans ce tableau, et illustré par la figure 4.1 :
Nom
module de z
argument de z
partie réelle de z
partie imaginaire de z
axe des réels
axe des imaginaires
(complexe) conjugué de z
plan complexe
Signification
longueur r de z
angle θ de z
abscisse du point d’affixe z
ordonnée du point d’affixe z
ensemble des nombres réels
ensemble des nombres imaginaires
symétrique de z par rapport à l’axe des réels
ensemble des nombres complexes
Notation
|z|
arg(z)
<(z)
=(z)
R
iR
z
C
Selon le point de vue géométrique, on définit l’addition de deux nombres complexes comme l’affixe du
−−→
−−→
vecteur somme. Si z1 et z2 sont les affixes respectives des vecteurs OM et ON , alors z1 + z2 est définie
−−→ −−→
comme l’affixe du vecteur OM + ON . Le produit de deux nombres complexes est défini de telle sorte que
les arguments des deux complexes s’additionnent. De plus, les modules sont également multipliés. Si z1 z2
−−→
est l’affixe du vecteur OP , alors OP = OM × ON et arg(z1 z2 ) = arg(z1 ) + arg(z2 ), où arg(z1 z2 ) est l’angle
−−→
entre OP et l’axe des réels positifs.
L’écriture algébrique x + yi des nombres complexes n’est pas adaptée à leur multiplication. C’est
pourquoi on choisit d’utiliser un autre système de coordonnées pour définir un point du plan complexe, et
donc une autre notation.
Définition 2. Soit un repère orthonormé d’origine O, et un point M du plan. L’écriture polaire de l’affixe
−−→
z de M est donnée par z = (r, θ) ou z = r∠θ, où r est la distance OM et θ l’angle entre le vecteur OM
et l’axe des réels positifs. On a z = |z| ∠ arg(z).
32
Figure 4.1 – Illustration des notions liées à un nombre complexe.
axe des imaginaires
z = x + iy = r∠θ
|z |
y = =(z)
r=
θ = arg(z)
0
axe des réels
x = <(z)
C
z = x − iy
Avec cette écriture, la multiplication de deux nombres complexes devient :
(r∠θ) × (r0 × θ0 ) = (rr0 )∠(θ + θ0 )
Exemple. Soit i = 0 + i1 le nombre complexe traditionnel. On voit, géométriquement, que le vecteur
correspondant à i est de longueur 1 et forme un angle de π2 avec l’axe des réels, donc i = 1∠ π2 . Avec cette
définition de la multiplication, on a
π
π
i2 = i × i = (1∠ ) × (1∠ ) = 1∠π = −1,
2
2
donc i2 = −1 : le nombre i est une racine carrée de −1 ! Vous pouvez vérifier que −i est l’autre racine
carrée de −1.
Remarques
√
– Plus généralement, tout nombre complexe a une racine carrée : une racine carrée de R∠θ est R∠ θ2 .
– Les nombres réels s’écrivent sous la forme r∠0 ou r∠π selon qu’ils sont positifs ou négatifs. Les
π
nombres imaginaires purs sont de la forme r∠ ± .
2
– Les angles étant définis à 2π près, on a r∠θ = r∠(θ + 2π) = r∠(θ − 2π) = . . ..
Proposition 3. Soit z = x + iy un nombre complexe non nul. Alors,
tan(arg(z)) =
y
,
x
z = R∠θ = R cos(θ) + iR sin(θ).
Preuve. Soit z un nombre complexe non nul, on l’écrit z = R∠θ. Alors, les relations de trigonométrie
dans le triangle T donnent
cos(θ) =
côté adjacent
x
= ,
hypoténuse
R
donc x = R cos(θ), y = R sin(θ) et tan(θ) =
sin(θ)
cos(θ)
sin(θ) =
= xy .
côté opposé
y
= ,
hypoténuse
R
√
Exemple 1. On a 1 + i = 2∠ π4 . En effet, tan(arg(1 + i)) = 1 = tan π4 , donc arg(1 + i) = π4 à un
multiple de π près (la fonction tangente est périodique de période π), donc arg(1 + i) = π4 ou 5π
4 . Mais
33
Figure 4.2 – Addition et produit (géométriques) de deux nombres complexes.
P (z + z 0 )
M (z)
N (z 0 )
O
P (zz 0 )
|z | ×
0
|z |
M (z)
N (z 0 )
O
1 + i est dans le quadrant supérieur droit du plan, donc son argument ne peut pas être
forme, il est aisé de voir que (1 + i)4 = −4, car
√
2∠
5π
4 .
Sous cette
π 4 √ 4
π
= 2 ∠4 · = 4∠π = −4.
4
4
√
3
1
Exemple 2. On a 1∠ 2π
3 = 2 + i 2 . Notons que cet exemple a été choisi parce que la forme polaire
permet de voir très aisément que ce nombre élevé à la puissance 3 donne 1. On a montré, à peu de frais,
√
3
que 23 + i 12
= 1 : il y a d’autres nombres complexes que 1 qui, élevés à la puissance 3, donnent 1,
alors qu’il n’y a qu’un seul nombre réel à le vérifier. Plus généralement, l’équation z n = 1 a exactement n
solutions au sein des nombres complexes.
Remarque. On peut montrer géométriquement que pour tout nombre complexe non nul z, il existe un
nombre complexe z 0 tel que zz 0 corresponde au point de coordonnées (1,0) (autrement dit, zz 0 = 1). On
note z1 ce nombre. Par exemple, 1i = −i. On définit alors la division d’un nombre complexe z par un
nombre complexe z 0 comme le produit z × z10 , noté zz0 .
4.2
Point de vue algébrique
On a déjà vu l’écriture algébrique (ou cartésienne) des nombres complexes : a + ib.
Définition 4. Soient deux nombres complexes z1 = x1 + iy1 et z2 = x2 + iy2 . Alors
z1 + z2 = (x1 + x2 ) + i(y1 + y2 )
et
z1 z2 = (x1 x2 ) + i(x1 y2 + y1 x2 ) + i2 (y1 y2 ) = (x1 x2 − y1 y2 ) + i(x1 y2 + y1 x2 )
Exemple. On a vu dans la section précédente que (1 + i)4 = −4 avec le produit géométrique. On peut
aussi le démontrer grâce au produit algébrique, mais c’est moins direct :
(1 + i)4 = (1 + i)2
2
= (1 + 2i + |{z}
i2 )2 = (2i)2 = 22 i2 = −4.
=−1
34
Proposition 5.Soit z = x + iy un nombre complexe. On a les égalités suivantes :
<(z) =
z+z
,
2
=(z) =
z−z
z−z
= −i
,
2i
2
|z|2 = zz = x2 + y 2 ,
z
1
= 2.
z
|z|
Figure 4.3 – Interprétation géométrique de la proposition 5.
z−z
i=(z)
z
z
<(z)
z+z
−z
0
z
z
Preuve. Par définition des parties réelle et imaginaire, si z = x + iy, on a x = <(z) et y = =(z). Alors,
(x + iy) + (x − iy)
2x
z+z
=
=
= x = <(z),
2
2
2
et de même :
z−z
(x + iy) − (x − iy)
2iy
=
=
= y = =(z).
2i
2i
2i
Montrons que zz = x2 + y 2 . On a :
+
zz = (x + iy)(x − iy) = (x2 − y · (−y)) + i(
−xy
xy)
= x2 + y 2 .
L’égalité |z|2 = x2 + y 2 provient (géométriquement) du théorème de Pythagore.
Enfin, partant de z1 , la multiplication aux numérateur et dénominateur par z donne le résultat voulu.
Remarque 1. Cette proposition donne une nouvelle identité remarquable : a2 + b2 = (a + ib)(a − ib)
(on applique la proposition à z = a + ib).
Remarque 2. Grâce à ces formules, on peut voir que si z = R∠θ, alors
1
z
=
1
R∠
− θ : on a
1
1
1
1
= z × 2 = (R∠ − θ) × ( 2 ∠0) = ∠ − θ.
z
|z|
R
R
En effet, |z| étant une distance, c’est en particulier un réel positif, donc son argument est nul.
Remarque 3. On a montré que si z = x + iy, alors
forme algébrique.
1
z
=
1
x+iy
=
x
x2 +y 2
y
− i x2 +y
2 : on sait mettre
1
z
sous
Corollaire 6.Un nombre complexe z est réel si, et seulement si z = z. Il est imaginaire pur si, et seulement
si z = −z.
Preuve. Un nombre complexe z est réel si, et seulement si =(z) = 0, si et seulement si
seulement si z = z. On procède de même pour les autres égalités.
z−z
2i
= 0, si et
Corollaire 7.Deux nombres complexes z et z 0 sont égaux si, et seulement si leurs parties réelle et imaginaire sont égales.
35
Preuve. Il est clair que si <(z) = <(z 0 ) et =(z) = =(z 0 ), alors z = z 0 . Inversement, si z = z 0 , alors
z = z 0 (ce sont les mêmes coordonnées que z et z’ au signe près), donc
<(z) =
z0 + z0
z+z
=
= <(z 0 ),
2
2
et de même pour =(z).
Enfin, on résume rapidement les propriétés vérifiées par la conjugaison et le module.
Proposition 8. Propriétés de la conjugaison. Soient z et z 0 deux nombres complexes. On a z = z,
z + z 0 = z + z 0 , zz 0 = zz 0 , et |z| = |z|.
Proposition 9. Propriétés du module. En plus de la propriété |z|2 = zz déjà citée, on a pour tous
nombres complexes z et z 0 :
– |zz 0 | = |z| · |z|0 , et si z 0 6= 0, zz0 = |z|z|0 | ;
– |z| = 0 si, et seulement si z = 0 ;
– |z ± z 0 | ≤ |z| + |z 0 | (inégalité triangulaire).
Preuve. Seule l’inégalité triangulaire est difficile à démontrer algébriquement, et découle de <(zz 0 ) ≤
|z| · |z 0 |.
Figure 4.4 – Inégalité triangulaire.
z + z0
z
z|
|z |
0
+
|z
z0
0
|z |
O
4.3
Exponentielle complexe
Définition 10. Il existe une unique fonction f dérivable, définie sur R, telle que pour tout x réel, f 0 (x) =
i · f (x), et f (0) = 1. On note x 7→ eix , la fonction vérifiant ces conditions.
Les propriétés de l’exponentielle réelle sont encore valables pour l’exponentielle complexe :
Proposition 11.Soient φ et θ deux réels. On a ei(φ+θ) = eiφ eiθ .
Alors, le théorème suivant permet de laisser de côté la notation R∠θ pour une bien meilleure (la forme
exponentielle).
Théorème 12.
Formule d’Euler Soit θ un nombre réel. On a
eiθ = cos(θ) + i sin(θ).
36
Figure 4.5 – Formule d’Euler illustrée.
π
ei 2 = i
reiθ
eiθ
θ
eiπ = −1
ei2π = 1
π
e−i 2 = −i
Preuve. La preuve revient à démontrer l’unicité annoncée dans la définition, on va la démontrer. Soit
eiθ
f (θ) = cos(θ)+i
sin(θ) . La fonction f est dérivable en tant que quotient de fonctions dérivables (à noter que
le dénominateur ne s’annule jamais). On a
f 0 (θ)
=
=
=
i · eiθ (cos(θ) + i sin(θ)) − eiθ (− sin(θ) + i cos(θ))
(cos(θ) + i sin(θ))2
+ i2 sin(θ) + sin(θ) − i cos(θ))
eiθ (
i cos(θ)
(cos(θ) + i sin(θ))2
iθ
e (− sin(θ) + sin(θ))
= 0.
(cos(θ) + i sin(θ))2
Donc f est une fonction constante, toujours égale à f (0) = 1. Ceci prouve que eiθ = cos(θ) + i sin(θ). Remarque
Avec cette représentation, la formule de multiplication géométrique pour les nombres complexes devient
presque évidente :
(Reiφ ) × (reiθ ) = Rrei(θ+φ) .
Figure 4.6 – Illustration de la formule eiθ eiφ = ei(θ+φ) .
eiφ
eiθ
φ
ei(θ+φ)
θ
θ
Les formules très intéressantes de l’exponentielle en induisent d’autres avec grande facilité. Une conséquence importante de la formule d’Euler est qu’en fait, les fonctions cosinus et sinus peuvent être définies
à partir de la fonction exponentielle. Plus précisément, les formules <(z) = z+z
et =(z) = z−z
2
2i vues
−iθ
précédemment donnent, grâce à la relation eiθ = e
:
Proposition 13.Pour tout réel θ, on a cos(θ) =
eiθ +e−iθ
,
2
Avant de conclure ce chapitre, plusieurs remarques :
37
et sin(θ) =
eiθ −e−iθ
.
2i
Figure 4.7 – Liens entre cos, sin et exp.
eiθ
0
θ
−θ
eiθ
2 cos(θ)
e−iθ
0
θ
−θ
2i sin(θ)
e−iθ
– On a évidemment, presque par définition, que arg(Reiθ ) = θ (le R compte pour du beurre, pourvu
qu’il corresponde bien au module d’un nombre complexe, c’est-à-dire à une quantité positive). Ainsi,
on peut retrouver plusieurs propriétés de l’argument en écrivant d’abord
les nombres complexes
évalués sous forme exponentielle. Par exemple, pour retrouver que arg z1 = − arg(z), on écrit que
z = Reiθ , et on utilise les propriétés de l’exponentielle pour trouver que
1 −iθ
1
1
= arg
= arg
e
= −θ = − arg(z).
arg
z
Reiθ
R
De la même manière, on retrouve que arg(zz 0 ) = arg(z) + arg(z 0 ), ou arg zz0 = arg(z) − arg(z 0 ).
– Dans les calculs, il est bon de savoir écrire zeiθ , où z est un nombre complexe, sous la forme
exponentielle Reiφ , en écrivant z sous sa forme exponentielle. Ça peut parfois simplifier des calculs ;
on tombe par exemple très souvent sur −eiθ (qui se réécrit ei(θ+π) ), ou ieiθ (qui se réécrit ei(θ+π/2) ).
38
4.4
4.4.1
Exercices
Entraînement au calcul de nombres complexes
Exercice 1. Soient z = 2 + 3i et z 0 = i − 5. Calculer et écrire sous forme algébrique z + z 0 , z − z 0 , 2z − 3z 0 ,
zz 0 , z 2 .
Exercice 2. Placer dans le plan complexe les points d’affixe
z1 = 2 + 3i, z2 = 3 + i, z3 = −1 + 2i, z4 = 2 − i, z5 = i,
z6 = −i, z7 = 1, z8 = −i − 3, z9 = 2z1 − 3z2 , z10 = z3 (z4 − z2 ).
Exercice 3.
a) Calculer (3 + 2i)(3 − 2i). En déduire la forme algébrique de
1
.
3 + 2i
1
1
1
,
et .
b) Déterminer la forme algébrique des nombres complexes
1+i 3−i
i
Exercice 4.
a) Écrire sous forme algébrique les nombres complexes suivants :
z1 =
2−i
1
4
i
2+i
, z3 =
, z2 = √
, z4 =
, z5 =
.
2 + 7i
5 + 3i
1 − 3i
i
3−i
b) Résoudre l’équation (1 + i)z = 3 − 2i, donner la solution sous forme algébrique.
c) Ecrire plus simplement le nombre complexe
√
√
7 + 5i
2 7 − 2i
+ √
z6 = √
2 7 − 2i
7 + 5i
Exercice 5. Conjugaison. Soit z = 3 + 5i et z 0 = −2 + 3i. Calculer z, z 0 , z + z 0 , z + z 0 , z + z 0 , zz 0 , zz 0 ,
zz 0 .
Exercice 6.
a) Calculer le module de chacun des nombres complexes
2
z1 = 3 + 4i, z2 = 1 − i, z3 = 5 − , z4 = 3
i
√
√
2
2
z5 = i − 4, z6 = i, z7 = −5, z8 =
+
i.
2
2
b) Donner les formes trigonométriques de
√
√
z1 = 1 + i, z2 = 3 + i, z3 = 1 − i 3, z4 = i.
Exercice 7. On considère les nombres complexes z1 = eiπ/3 , z2 = eiπ/4 et Z = zz21 .
a) Donner la forme exponentielle de Z.
b) Donner les formes algébriques de z1 et
. En déduire
π la forme algébrique de Z.
πz2
et sin
.
c) En déduire les valeurs exactes de cos
12
12
4.4.2
Exponentielle complexe et trigonométrie
Exercice 8.
a) Rapeller la forme trigonométrique du nombre complexe eiθ .
b) En utilisant les exponentielles complexes, retrouver les formules de développement de cos(θ + ϕ) et
sin(θ + ϕ).
Exercice 9.
a) En utilisant les exponentielles complexes, développer cos(3θ) et sin(3θ) respectivement en fonction de
cos(θ) et sin(θ). Pour rappel, (a + b)3 = a3 + 3a2 b + 3ab2 + b3 .
b) A l’inverse, exprimer (cos(θ))4 et (sin(θ))4 en fonction de cos(4θ) et cos(2θ). Pour rappel : (a + b)4 =
a4 + 4a3 b + 6a2 b2 + 4ab3 + b4 .
Exercice 10. Soit z = 1 + i tan(θ). Quel est l’argument de z ? En développant z 3 , déterminer tan(3θ).
39
4.4.3
Utilisation des complexes pour la géométrie 2D
On utilisera dans les prochains exercices les propositions suivantes, qui permettent de faire de façon
simple de la géométrie en quelques opérations sur des nombres complexes.
Proposition 1. Affixe d’un vecteur. Soient A et B deux points du plan, d’affixes respectives a et b.
−−→ −−→
Alors, on a AB = OM pour M d’affixe b − a.
−−→
Autrement dit, si on veut travailler sur le vecteur AB avec le point de vue des nombres complexes, on
−−→
doit traduire AB en b − a.
−−→ −−→
−−→ −→ −−→
−→ −−→
−→
Preuve. Si OM = AB, alors OM = AO + OB = −OA + OB par la relation de Chasles. Comme OA a
−−→
−−→
pour affixe a, et OB pour affixe b, on en déduit que OM a pour affixe −a + b.
−−→
Proposition 2. Norme d’un vecteur. Soient A et B deux points du plan. Alors, la norme de AB est
|b − a|.
Preuve. C’est évident, grâce à la proposition précédente et la définition du module d’un nombre complexe.
→
−
→
−
Proposition 3. Angle entre deux vecteurs
Soient u et v deux vecteurs, d’affixes a et b. Alors,
−
−
l’angle orienté entre →
u et →
v est égal à arg b = arg(b) − arg(a).
a
−
−
Preuve. On peut toujours supposer que →
u et →
v ont pour extrémité
O. Un dessin rend alors clair que
→
−
→
−
l’angle entre u et v égale arg(b) − arg(a), et ceci égale arg ab grâce aux propriétés de la multiplication
complexe.
Figure 4.8 – Angle entre deux vecteurs.
~v
arg(b) − arg(a)~u
arg(b)
arg(a)
Enfin, il est souvent utile de savoir reconnaitre l’équation d’un cercle.
Proposition 4. Équation d’un cercle. Soit I un point d’affixe ω, et R un réel positif. Les points M
d’affixe z qui sont sur le cercle de centre I et de rayon R vérifient :
|z − ω| = R.
Preuve. Être sur un tel cercle signifie que IM = R, et donc, grâce à la proposition 2, que |z − ω| = R.
√
√
Exercice 11. Soient les points A, B et C d’affixes respectives a = 1 + 3 + 2i, b = 1 − 3 + 2i et c = 1 − i.
−−→ −→
a) Déterminer les affixes des vecteurs AB et AC, ainsi que leurs modules. Que dire du triangle ABC ?
−−→ −→
b) Calculer l’angle entre les vecteurs AB et AC. Que dire du triangle ?
Exercice 12. Soient les points A, B et C d’affixes −1 − i, 3 − 2i et 7 − 3i. Montrer que ces points sont
alignés.
Exercice 13.Soit j = ei2π/3 .
a) Montrer que
1 + j + j2 =
j3 − 1
= 0.
j−1
b) Soient M1 , M2 et M3 les points d’affixes 1, j et j 2 . Que dire du point O par rapport au triangle
M1 M2 M3 ?
40
On se propose de montrer dans la suite de l’exercice que si a, b et c sont les affixes distinctes de trois
points A, B et C, alors on a :
ABC est un triangle équilatéral ⇔ a + bj + cj 2 = 0
c) Donner les conditions nécessaire et suffisante sur le complexe
équilatéral.
d) Montrer que
c + a(eiπ/3 − 1) + bei4π/3 = 0.
c−a
b−a
pour que le triangle ABC soit
e) Montrer que eiπ/3 − 1 = j : i) en utilisant la forme algébrique. ii) en factorisant par l’exponentielle de
la moyenne des arguments (ici eiπ/6 ).
f) En se souvenant que j 3 = 1, retrouver l’équivalence recherchée.
Exercice 14. Soit Q un quadrilatère quelconque, et construisons des carrés sur les côtés de ce quadrilatère,
comme indiqué sur la figure 4.9.
Figure 4.9 – Un quadrilatère et ses carrés adjacents
P
O
2a
S
2d
2b
2c
Q
R
L’exercice est de prouver que les segments joignant les centres des carrés opposés sont perpendiculaires,
et sont de même longueur, comme cela semble être le cas sur la figure. On désigne par 2a, 2b, 2c et 2d
les affixes des vecteurs formant les côtés du quadrilatère. On fixe l’origine du repère au sommet où 2a
commence, c’est-à-dire le point O sur la figure.
a) Que dire de la somme a + b + c + d ?
b) Déterminer, en fonction de a, l’affixe du point P . Procéder de même pour déterminer les affixes des
points Q, R et S.
−→ −→
c) Calculer les affixes z1 et z2 des vecteurs P R et SQ.
d) Conclure.
41