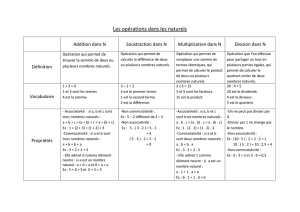
AXIOMES (ou REGLES) DE CALCUL

AXIOMES (ou REGLES) DE CALCUL
Dans tous les ensembles de nombres, naturels (N), entiers relatifs (Z), décimaux relatifs (D),
rationnels (les fractions ou Q) et réels ( R), quels que soient ses éléments a, b et c on a :
a + b = b + a la commutativité de l’addition
(a + b) + c = a + b + c = a + (b + c) l’associativité l’addition
0 + a = a 0 est appelé l’élément neutre additif
a · b = b · a la commutativité de la multiplication
(a · b) · c = a · b · c = a · (b · c) l’associativité de la multiplication
1 · a = a 1 est appelé l’élément neutre multiplicatif
la distributivité de la multiplication sur
l’addition, valable aussi bien pour la
soustraction a·(b – c) = a·b – a·c.
Lue de gauche à droite, on dit que l’on a développé le produit a·(b + c) en une somme a·b + a·c.
Lue de droite à gauche, on dit avoir factorisé la somme ou avoir mis en évidence le facteur a.
4 exemples d’utilisation pour réduire des expressions algébriques.
Si x et y représentent des nombres quelconques alors
2x + 3x = 2·x + 3·x = (2 + 3)·x = 5x par la distributivité
2x·3x = 2·3·x·x = (2·3)·(x·x) = 6·x2 par commutativité et associativité de ·
2x + 3y + 5x + 7y = 2x + 5x + 3y + 7y = par la commutativité et la distributivité
= (2 + 5)x + (3 + 7)y = 7x + 10y
3x + x = 3x + 1·x = (3 + 1)·x = 4·x utilisation élément neutre et distributivité
Dans l’ensemble des nombres relatifs (entiers, décimaux, rationnels et réels) tout élément n admet
un opposé noté -n qui vérifie la propriété n + (-n) = 0. À l’aide des règles précédentes on peut
démontrer :
-(-n) = n l’opposé de l’opposé d’un nombre = le nombre
a – b = a + (-b) soustraire un nombre (b) = additionner son opposé (-b)
-n = (-1)·n l’opposé d’un nombre = le produit du nombre par -1
Exemples d’utilisation pour réduire. Si a, b, x et y représentent des nombres quelconques alors
-a – b = (-1)·a + (-b) = (-1)·a +(-1)·b = (-1)·(a +b) = -(a + b)
(-a)·(-b) = (-1)·a·(-1)·b = (-1)·(-1)·a·b ={ (-1)[(-1)]}a·b = a·b
2x – 3y – 5x + 7y = 2x + (-3y) + (-5x) + 7y = 2x + (-5x) + (-3y) + 7y = = -3x + 4y
-(2x – 3y) – 5x = (-1)·[2x + (-3y)] + (-5x) = (-1)·2x + (-1)·(-3y) + (-5x) = -2x + 3y + (-5x)
= -2x + (-5x) + 3y = (-2 + -5)·x + 3y = -7x + 3y