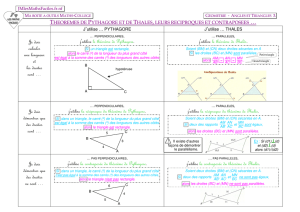
ch2-Le theoreme de Thales

Page 1 sur 7
C HAPITRE 2 Q UELQUES THEOREMES VUS EN 4
EME
L E THEOREME DE T HALES ET SA RECIPROQUE
I. Q UELQUES THEOREMES VUS EN 4
EME
 E XERCICE 1
ABC est un triangle rectangle en A. AB = 5 cm et BC = 6 cm
Calculer AC à 0,1 cm près.
Solution :
On sait que : …………………………………………………………
On utilise : ……………………………………………………………
On conclut : …………………………………………………………..
 E XERCICE 2
RST est un triangle tel que
RS = 6 cm, RT = 2,5 cm et ST = 6,5 cm.
Démontrer que ce triangle est rectangle.
Solution :
On sait que : ……………………………………………………………….
On utilise : ………………………………………………………………….
On conclut : ………………………………………………………………..

Page 2 sur 7
 E XERCICE 3
EFG est un triangle rectangle en E tel que EF = 5 cm et FG = 6 cm.
I est le milieu de [FG]. Calculer EI.
Solution :
On sait que : ………………………………………………………………..
On utilise : …………………………………………………………………...
…………………………………………………………………………………
………………………………………………………………………………….
On conclut : …………………………………………………………………
 E XERCICE 4
TUV est un triangle tel que TU = 4 cm, TV = 5 cm et UV = 6 cm.
I est le milieu de [TU] et J celui de [TV]. Calculer IJ
Solution :
On sait que : …………………………………………………………
On utilise : ……………………………………………………………
…………………………………………………………………………
………………………………………………………………………….
On conclut : ………………………………………………………..
 E XERCICE 5
RST est un triangle tel que RS = 8 cm, RT = 6 cm et ST = 7 cm.
M est le point du segment [RS] tel que SM = 5 cm.
La droite qui passe par M et qui est parallèle à (RT) coupe (ST) en N.
Calculer SN et MN.
Solution :
On sait que : …………………………………………………………
On utilise : ………………………………………………………….
On conclut : ………………………………………………………..

Page 3 sur 7
 E XERCICE 6
( c ) est un cercle de centre O et de rayon 3 cm.
[AB] est un diamètre de ( c ).
E est un point de ( c ) tel que AE = 5 cm.
Démontrer que ABE est un triangle rectangle.
Solution :
On sait que : …………………………………………………………
On utilise : ………………………………………………………….
…………………………………………………………………………..
………………………………………………………………………….
On conclut : ………………………………………………………..
II. L E THEOREME DE T HALES
A. T HEOREME ( ADMIS )
E ∈ [OA] O ∈ [EA]
F ∈ [OB] O ∈ [FB]
Dans les deux configurations :
SI les droites (EF) et (AB) sont parallèles ALORS les quotients OE
OA , OF OB et EF AB sont
égaux.
Autrement dit :
Si (EF) // (AB) alors OE
OA = OF OB = EF AB
Note : le sommet commun aux deux triangles (le point O) apparaît 4 fois dans les
quotients.

Page 4 sur 7
B. A PPLICATION
 Enoncé :
O ∈ [CB]
O ∈ [DA]
(CD) // (AB)
Calculer OB et OD
 Solution :
On sait que : O ∈ [CB] O ∈ [DA] et (CD) // (AB)
On utilise : le théorème de Thalès
On conclut : OC
OB = OD OA = CD AB
Appelons x et y les mesures en cm des longueurs OB et OD, on obtient :
5
x = y 9,5 = 4 6
Calcul de OB Calcul de OD
5
x = 4 6 y 9,5 = 4 6
4 × x = 5 × 6 y × 6 = 4 × 9,3
x = 5
× 6
4 y = 4
× 9,3
6
x = 7,5 y = 6,2
La longueur OB est égale à 7,5 cm. La longueur OD est égale à 6,2 cm.
III. R EGLES DES PRODUITS EN CROIX
A. R EGLE
a
b = c d est équivalent à a×
××
×d = b×
××
×c

Page 5 sur 7
B. A PPLICATIONS
 Application à la résolution d’équations :
Enoncé : Résoudre l’équation 3
x = 2 7
Solution : 3
x = 2 7
2 × x = 3 × 7
x = 3
× 7
2
x = 10,5
L’équation a une solution : 10,5
 Application à la comparaison de deux quotients:
Enoncé : Les quotients 6
14 et 9 21 sont-ils égaux ?
Solution : Calculons les deux produits en croix
6 × 21 = 126 et 9 × 4 = 126
Les produits en croix sont égaux donc les quotients aussi : 6
14 = 9 21 .
IV. R ECIPROQUE ET CONTRAPOSEE DU THEOREME DE THALES
A. U N PEU DE LOGIQUE
Théorème : Si A alors B
Réciproque : Si B alors A
Contraposée : Si non B alors non A
Les activités faites en classe on permis de montrer que :
- la contraposée d’un théorème est toujours vraie (en fait, la contraposée est une
autre formulation du théorème)
- la réciproque n’est pas toujours vraie : pour certains théorèmes elle est vraie, pour
d’autres elle est fausse.
Pour le théorème de Thalès, comme pour le théorème de Pythagore, la réciproque est
vraie (admis).