Exercice 1 Corrigé bac Blanc LUT S 2014 Exercice 2 - e

Exercice 1 Corrigé bac Blanc LUT S 2014
Exercice 2
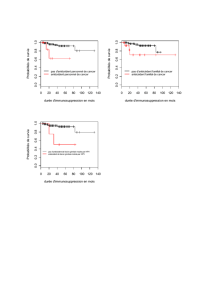
4. En moyenne, il devrait y avoir E(X) = np = 400x0,1= 40 personnes avec une malformation parmi ces 400 personnes

Exercice 3
Exercice 3
en +

Exercice 4 : 1°) Equation 2z² - 2z – 3 = 0 On a  = (-2)² - 4 (2) (-3) = 4+24= 28 = (2 )² > 0 donc 2 solutions réelles
z1 (ou x1) = et z2 (ou x2) =
2°) Soit f la fonction définie sur l’ensemble des nombres complexes par f(z) =
a) La fonction f admet-elle des valeurs interdites ? oui, il faut avoir 2z-1 0 donc z ½ . C’est la valeur
interdite. On notera K le point d’affixe ½
b) Image par f de z1 = 1+ i ? On a f(1+i) = = = = = -
et de z2 = 4i ? On a f(4i) = = = -
c) Points invariants par f ? On cherche donc les z tels que f(z) = z  z =  z(2z-1)= z+3  2z²-2z-3=0
D’après la première question, les points invariants sont donc z1 = et z2 =
3°) a) Antécédent de 0 par f ? On cherche donc les z tels que f(z) = 0  z+ 3 = 0 d’où z = -3
b) Antécédent de 1 par f ? On cherche donc les z tels que f(z) =1  = 1  z+3 = 2z – 1 z = 4
c) ½ a-t-il un antécédent par f ? On cherche donc les z tels que f(z) = ½  = ½  z + 3 = ½ (2z – 1) = z – ½
Cette équation n’a pas de solution donc ½ n’a pas d’antécédent par f.
4°) En posant z = x + iy, déterminer la partie réelle et la partie imaginaire de f(z).
On obtient f(z) = = = +
On a donc x’ = Re(f(z)) = et y’ = Im(f(z)) =
a) Ensemble E des points M(z) tel que f(z) soit réel : on doit avoir y’= 0 => -7y = 0 donc y = 0
E est donc la droite d’équation y = 0 (donc l’axe des x), privée du point K( ½ ), car c’est la valeur interdite.
b) Ensemble F des points M(z) tels que f(z) soit imaginaire pur :
on doit avoir x’= 0 => 2x² + 5x – 3 + 2y² = 0 soit, en divisant par 2 : x² + x + y² = puis
(x + )² - + y² = donc (x + )² + y² = + = = ( )²
F est donc le cercle C de centre ( - ; 0) et de rayon R = , encore privé du point K( ½ )
5°) a) b) zA = 2 – 2i son module est = = 2 d’où zA = 2 ( – i )= 2 ( cos(- ) + i sin(- ))
et zB = - 1 – i son module est = d’où zB = 2 ( ) = 2( cos(- ) + i sin(- ))
c) Distance AB = le module de zB- zA
Or zB- zA = - 1 – i - (2 – 2i ) = -3 + i( 2- ) donc
AB = = =
AB =
AB
Exercice 4