1. Présentation

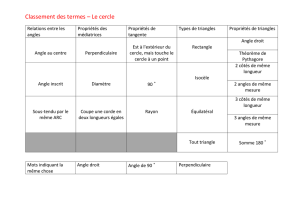
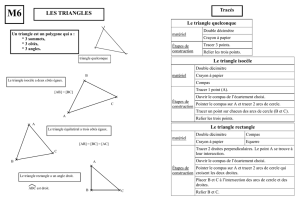
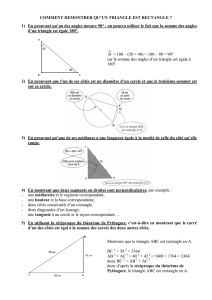
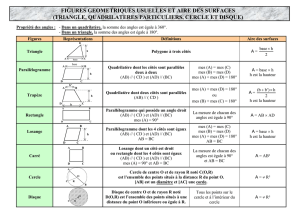
1. Présentation
1.1 Présentation et repères historiques
Les documents dont nous disposons à ce jour permettent de faire remonter
les recherches quantitatives sur les questions géométriques aux
Mésopotamiens et aux Egyptiens. Ainsi, le scribe égyptien Ahmès décrit
dans un document datant de 1650 avant J.C. une quadrature(1)
approximative du cercle, correspondant à un valeur de π proche de 3,16.
L'école de Platon a joué un rôle apparemment crucial dans les restrictions
imposées à la construction des figures, et particulièrement dans l'importance
accordée à l'usage préférentiel de la règle et du compas. On ne connaît pas
clairement les raisons qui ont imposé ce choix. Il se peut qu'une philosophie
basée sur l'idée que le cercle était une figure "parfaite" ait joué son rôle.
(1)
Quadrature du cercle : on réalise la quadrature du cercle en construisant un carré de même
aire qu'un cercle donné .
Les mathématiciens grecs ont laissé à la postérité notamment quatre problèmes célèbres : la duplication du
cube, la trisection de l'angle, la construction de polygones réguliers et la quadrature du cercle.
La duplication du cube constitue un problème très naturel puisque la
duplication du carré était un exercice de base et trouve sa source dans
une légende .
Pressé d’enrayer une épidémie de peste, l’oracle du temple d’Apollon
exigea la construction, à Délos, d’un temple double du précédent.
Eratosthène raconte que "Minos, voulant élever un monument à son fils
Glaucus, dit à l’architecte:
Tu as désigné certes un petit enclos pour la tombe d’un roi; qu’il soit
double; sans détruire ses belles proportions, double donc au plus tôt
chaque côté de la tombe.
Bien sur cette solution était fausse.
En clair, il s’agit de construire un volume V2 double d’un volume V1
donné.
Le problème de la trisection de l'angle s'ensuivait simplement de la construction de
la bissectrice.
La construction de polygones réguliers était peut-être issu de considérations pythagoriciennes; il semble en
effet que la pentagone régulier était un symbole mystique pour les pythagoriciens, qui connaissaient peut-être sa
construction à la règle et au compas; celle-ci était en tout cas connue d'Euclide au troisième siècle avant J.C. La
construction de polygones réguliers est bien sûr liée au calcul du nombre π ; c'est d'ailleurs ainsi qu'Archimède
obtient ses approximations.
Le problème de la quadrature du cercle relève de la même préoccupation : il est
facile de vérifier qu'elle équivaut à la construction à la règle et au compas de deux
segments dont le rapport des longueurs est π.
En 1796, Gauss montre que le polygone à 17 côtés est constructible à la règle et
au compas. Sa méthode algébrique ouvre l'étude moderne de ces questions.
En 1837, Wantzel caractérise les coordonnées des points que l'on peut construire à la
règle et au compas: les longueurs constructibles sont celles qui s'expriment à partir
des entiers à l'aide des 4 opérations et de l'extraction de racines carrées.
Wantzel en déduit que la duplication du cube et la trisection de l'angle sont impossibles à la règle et au
compas.
Enfin en 1882 Lindemann montre l'impossibilité de la quadrature du cercle.
1.2 Principes de bases
Les seuls outils de géométrie autorisés dans cette partie du cours étant la règle (non graduée) et le compas , les
seuls opérations permises à partir d'éléments de départ indiqués sont :
tracer une droite (ou une demi-droite ou un segment) passant par deux points connus ;
tracer un cercle (ou un arc de cercle) dont le centre est un point connu et passant par un point connu ;
prendre un écartement au compas égal à la distance entre deux points connus ;
tracer un point sur une droite (ou une demi-droite ou un segment)connue ;
tracer un point sur un cercle (ou un arc de cercle) connu ;
tracer le point d'intersection de deux droites connues ;
tracer un point d'intersection d'une droite et d'un cercle connus ;
tracer un point d'intersection de deux cercles connus .
2. Constructions élémentaires à partir de deux points de bases A et B
2.1 Droite (AB) , demi-droite [AB) ou segment [AB]
Deux points distincts A et B sont donnés .
On peut à l'aide de la règle seule tracer la droite (AB) ou la demi-droite [AB) ou le segment [AB] .
Droite (AB)
Demi-droite [AB)
2.2 Cercle de centre A passant par B
Deux points distincts A et B sont donnés .
On peut à l'aide du compas seul tracer le cercle de
centre A passant par B .
Segment [AB]
2.3 Cercle de centre A et de rayon BC
Trois points distincts deux à deux A , B et C sont
donnés .
On peut à l'aide du compas seul tracer le cercle de
centre A et de rayon BC .
2.4 Propriété caractéristique de la médiatrice d'un segment
Etant donnés deux points distincts A et B , la
médiatrice du segment [AB] est la droite
perpendiculaire à (AB) et passant par le milieu du
segment [AB] .
On peut également la caractériser comme l'ensemble
des points équidistants de A et de B.
Autrement dit , si un point M est équidistant de A et de B , il
appartient à la médiatrice de [AB] .
Réciproquement , si M un point M appartient à la médiatrice de
[AB] , il est équidistant de A et de B .
B
A
B
A
Conséquence : à partir de deux points distincts A et B , on peut tracer la médiatrice du segment [AB] en
traçant deux points M et M' , chacun étant point d'intersection de deux cercles de centres respectifs A et B et de
même rayon .
Exemple d'utilisation : étant donnés deux points distincts A et B du plan , tracer la perpendiculaire à (AB)
passant par A .
3. Constructions élémentaires à partir de trois points de bases
3.1 Bissectrice d'un angle
Soient A , B et C trois points non alignés du plan
et D un point du plan distincts de A , B ou C .
On dit que la droite (AD) est la bissectrice de l'angle

BAC si les angles 
BAD et 
DAC sont égaux .
3.2 Bissectrice et distance
Si un point M appartient à la bissectrice de 
BAC , il est équidistant des
droites (AB) et (AC) .
3.3 Bissectrices d'un triangle , cas du triangle isocèle
Dans un triangle , les bissectrices sont concourantes en un point I appelé centre du
cercle inscrit au triangle .
Si ABC est un triangle isocèle en A , la bissectrice de l'angle est également la
médiatrice de [BC] , la hauteur issue de A et la médiane issue de A .
3.4 Conséquence : construction de la bissectrice d'un angle à la règle et au compas .
Pour construire la bissectrice de l'angle 
BAC , on peut procéder comme suit :
Trois points A , B et C sont donnés .
Toujours à l'aide du compas , on trace un point P3 équidistant
de P1 et P2 .
A l'aide du compas , on trace deux points P1 et P2 situés sur (AB)
et (AC) respectivement et équidistants de A .
A l'aide de la règle , on peut tracer la droite (AP3) qui est la
bissectrice de l'angle 
BAC .
3.5 Triangles isométriques
On dit que deux triangles ABC et DEF sont isométriques si leurs côtés sont
égaux chacun à chacun (c'est-à-dire que AB = DE , BC = EF et CA = FD) .
Deux triangles isométriques ont leurs angles égaux chacun à chacun
 D
 ; B=
 E et C = F ) .
(c'est-à-dire que A=
3.6 Conséquence : «report» d'un angle à la règle et au compas.
Trois points A , B et C sont donnés .On considère un point D .
On peut construire à la règle et au compas deux points E et F tels que : 
BAC =
EDF comme suit :
A l'aide du compas , on tracer le cercle (C1) de centre D et de
rayon AB
On construit un point E sur ce cercle
A l'aide du compas , on trace le cercle (C2) de centre E et de
rayon BC et le cercle (C3) de centre D et de rayon CA .
On construit le point F comme point d'intersection de (C2) et (C3)
.
Exemple d'utilisation :
On donne un triangle ABC isocèle en A et D un point extérieur à ce triangle .
Tracer à la règle et au compas le point D ' , image de D par la rotation de centre A qui envoie B sur C .
4. Utilisations des propriétés sur les angles
4.1 Angle au centre
Soit (C) un cerce de centre O .
On considère trois points A , B et C situés sur ce cercle .
L'angle 
AOC est le double de l'angle 
ABC .
4.2 Angle inscrit
Un cercle (C) est donné .
On considère deux points A et B situés sur ce cercle .
Si M et N sont deux points situés sur un même arc de cerce
d'extrémités A et B , alors les angles 
AMB et 
ANB sont
égaux .
4.3 Conséquence : construction d'un point M tel que 
BAC =
BMC à partir de
trois points A , B et C .
On donne trois points A , B et C non alignés .
On peut construire à la règle et au compas un point M tel que 
ACB=
AMB comme suit :
On trace la médiatrice d'un côté du triangle ABC
... puis d'un deuxième
Le point d'intersection de ces deux droites est le centre du cercle
circonscrit au triangle ABC .
En prenant M sur l'arc de cercle d'extrémités A et B contenant le
point A , on obtient 
BAC=
BMC .
5. Utilisation du théorème de Thalès et des triangles semblables
5.1 Construction de la parallèle à une droite (D) passant par un point A
Une droite (D) et un point A n'appartenant pas à (D) sont donnés .
On peut construire à la règle et au compas la parallèle à (D) passant par A comme suit :
On trace un point M sur la droite (D)
On trace le point d'intersection N de (D) et du cercle de centre M
passant par A
On trace le point d'intersection P des cercles de centres A et N
et de rayon AM
Le quadrilatère AMNP étant un losange , les droites (AP) et (D)
sont bien parallèles .
5.2 Théorème de Thalès
On considère cinq points A , B , C , D et E .
On suppose que :
les droites (BC) et (DE) sont parallèles
les points A , B , D et les points A , C , E sont alignés dans le même ordre .
Les hypothèses indiquées ci-dessus reviennent à dire que l'on a l'une des figures-clé ci-dessus .
On sait d'après le théorème de Thalès que
AB AC BC
=
=
AD AE DE
.
5.3 Exemple d'utilisation : partager un segment [AB] donné en n segments de même
longueur
On peut partager un segment [AB] en n segments isométriques de la façon suivante :
On trace un point M1 à n'appartenant pas à la droite (AB) .
On trace n–1 points M2 , M3 , ... , Mn tels que chaque segment
Mp-1Mp ait pour longueur AM1.
On trace la droite (BMn) , puis les parallèles à (BMn) passant
par M1 , M2 , .....
En traçant les points d'intersections de ces droites avec le
segment [AB] , on obtient bien n segments de même longueur
5.4 Triangles semblables
On dit que deux triangles ABC et A’B’C’ sont semblables s’ils ont
la même forme , ce qui signifie que les angles de l’un sont égaux aux
angles de l’autre chacun à chacun .
Exemples :
l Deux triangles équilatéraux sont nécessairement semblables .
l Deux triangles rectangles et isocèles sont nécessairement
semblables .
Si deux triangles ABC et A’B’C’ sont semblables , alors leurs côtés homologues sont proportionnels ,
A' B' A' C'
B'C'
c’est-à-dire que les rapports
;
et
sont tous égaux à un même réel k .
AB
AC
BC
l Réciproquement , si deux triangles ABC et A’B’C’ ont leurs côtés homologues proportionnels , ils sont
semblables .
Dans tous les cas , le coefficient de proportionnalité k est appelé rapport de similitude .
Remarque : n si 0 < k < 1 , A’B’C’ est une réduction du triangle ABC .
n si k > 1 , A’B’C’ est un agrandissement du triangle ABC .
n si k = 1 , A‘B’C’ et ABC sont isométriques .
l
5.5 Angles de même mesure
Soient (D) et (D') deux droites parallèles
et (D2) une droite sécantes à (D) et (D') .
Les angles indiqués sur la figure ci-contre ont même mesure .
angles correspondants
angles alternes internes
angles alternes externes
5.6 Construction d'un triangle DEF semblable à un triangle ABC
Un triangle ABC est donné.
On considère deux points D et E situés à l'extérieur du triangle ABC .
On peut construire un triangle DEF semblable au triangle ABC comme suit :
On trace un point E' sur la droite (DE) tel que DE' = AB
On construit le point F' tel que E'F' = BC et DF' = AC.
Les triangles DE'F' et ABC sont donc isométriques .
Grâce aux propriétés des triangles isométriques , on sait que les
angles aux sommets sont identiques dans ces deux triangles .
Le point F est obtenu en construisant le point d'intersection de
(DF') et de la parallèle à (E'F') passant par E .
6. Utilisation des transformations usuelles
6.1 Isométries
On appelle isométrie une transformation du plan qui conserve les longueurs .
Les transformations usuelles (translation , symétrie axiale , réflexion , rotation) sont des isométries .
6.2 Images de figures usuelles
L'image d'une figure F (triangle , cercle , parallélogramme , losange , rectangle , carré , ...) par une isométrie est
une figure (F') superposable à la figure initiale.
Elles sont donc de même nature et de même dimensions , donc de même aire .
Les isométries conservent le parallélisme , l'orthogonalité et les angles géométriques.
(C') est l'image de (C) par la translation de T ' est l'image de T par la symétrie centrale
vecteur 
de centre O
AB .
P' est l'image du carré P par la rotation de
centre O et d'angle 60° .
Exemple d'utilisation : On se donne trois droites parallèles (D1) , (D2) et
(D3) . On veut construire un triangle ABC équilatéral de telle sorte que A
appartienne à (D1) , B à (D2) et C à (D3) .
On raisonne à partir d'une figure déjà construite :
Dire que ABC est équilatéral revient à dire que le point C est l'image du point B par la rotation r de centre A et d'angle 60° .
Comme B appartient à (D2) , son image C par r appartient à l'image de (D2) par r .
Comme C appartient également à (D3) , il est le point d'intersection de (D3) et de r(D2) .
On trace le point A sur la droite (D1) , deux points M et N sur (D2)
On trace deux triangles équilatéraux AMM' et ANN' ;
la droite (M'N') est l'image de (D2) par r : elle coupe la droite (D3)
en C .
On construit alors le point B , troisième sommet du triangle
équilatéral ABC .
6.3 Image d'une intersection
On considère deux figure (F1) et (F2) transformées respectivement en (F1') et (F2') par une isométrie .
Si un point M appartient à l'intersection de (F1) et de (F2) , alors son image M' appartient à l'intersection de (F1')
et de (F2') .
7. Nombres constructibles
7.1 Définition
Le plan est rapporté à un repère orthonormal O ; i ; j  .
Un nombre réel est dit constructible si c'est l'une des coordonnées d'un point M constructible à la règle et au
compas .
Exemples :
Comme les poins M1 et M2 ont pour coordonnées
respectives (3 ; 0) et (0 ; -2) , 3 et -2 sont
constructibles .
De façon générale , tout nombre entier est
constructible .
Le point M3 a pour coordonnées   2 ; 0 donc
 2 est constructible .
Remarque : si a est constructible , son opposé est
également constructible .
7.2 Somme et différence de deux nombres constructibles .
Si a et b sont deux nombres constructibles , alors :
a + b est constructible .
a - b est constructible .
Justification : supposons que a et b soient les abscisses de deux points A et B respectivement .
On peut construire un point M1 de coordonnées (a + b ; 0) et un point M2 de coordonnées (a - b ; 0) comme
suit :
7.3 Produit de deux nombres constructibles
Si a et b sont deux nombres constructibles , alors le produit a×b est constructible .
Justification : supposons que a et b soient des coordonnées de 2 points A et B respectivement (a > 0 , b > 0).
On peut construire un point M1 de coordonnées (a×b ; 0) comme suit :
On construit le point A' de coordonnées (a ; 0) et le point B' de
coordonnées (0 ; b) .
On trace la droite (d) la parallèle à (A'J) passant par B' .
Le point d'intersection de (OI) et (d) a pour
coordonnées (a×b ; 0) .
7.3 Inverse d'un nombre constructible non nul .
Soit a un nombre non nul .
Si a est un nombre constructible , alors l'inverse de a est également constructible .
Justification : supposons que a soit un nombre constructible strictement positif , abscisse d'un point A .
1
; 0 comme suit :
On peut construire le point M de coordonnées
a
 
On construit le point A' de coordonnées (a ; 0)
On construit le point M' d'intersection de la parallèle à (A'J)
passant par I et de l'axe des ordonnées .
Le point d'intersection du cercle de centre O et de
1
;0 .
rayon OM' a pour coordonnées
a
 
7.4 Racine carrée d'un nombre constructible
Soit a un nombre réel positif .
Si a est constructible , alors  a est également constructible .
Justification : On suppose que a soit l'abscisse d'un point A constructible à la règle et au compas .
Il suffit de construire dans l'ordre :
le point A' projeté orthogonal de A sur l'axe des abscisses ;
le point K tel que OK = 1 sur la partie de (OA') ne contenant pas
A' ;
un demi-cercle de diamètre [A'K] ;
l'intersection F de ce demi-cercle et de l'axe des ordonnées .
Le point F a pour coordonnées
0 ; a 
.
7.5 Grandeurs ou segments commensurables
On dit que deux segments sont commensurables si le rapport de leurs longueurs est un nombre rationnel , ce
qui revient à dire que l'on peut choisir une unité de longueur dans laquelle chaque segment a pour longueur un
nombre entier .
Exemple :
Sur la figure ci-contre , tous les cercles ont le même
rayon.
Les segments [AB] et [BC]s ont commensurables .