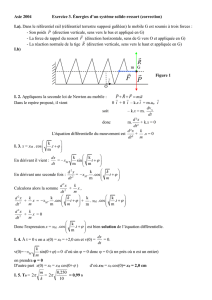
Chapitre 18
publicité
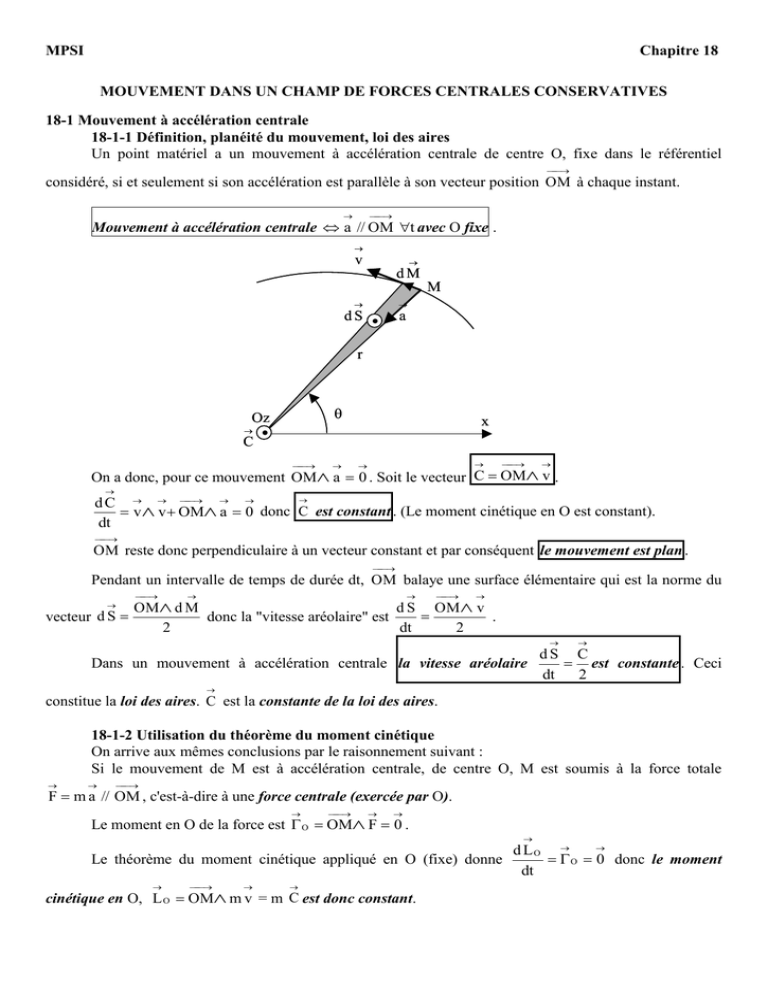
MPSI Chapitre 18 MOUVEMENT DANS UN CHAMP DE FORCES CENTRALES CONSERVATIVES 18-1 Mouvement à accélération centrale 18-1-1 Définition, planéité du mouvement, loi des aires Un point matériel a un mouvement à accélération centrale de centre O, fixe dans le référentiel considéré, si et seulement si son accélération est parallèle à son vecteur position OM à chaque instant. Mouvement à accélération centrale a // OM t avec O fixe . v dM M dS . a r Oz . C x On a donc, pour ce mouvement OM a 0 . Soit le vecteur C OM v . d C v v OM a 0 donc C est constant . (Le moment cinétique en O est constant). dt OM reste donc perpendiculaire à un vecteur constant et par conséquent le mouvement est plan . Pendant un intervalle de temps de durée dt, OM balaye une surface élémentaire qui est la norme du OM d M d S OM v vecteur d S donc la "vitesse aréolaire" est . 2 dt 2 dS C Dans un mouvement à accélération centrale la vitesse aréolaire est constante . Ceci dt 2 constitue la loi des aires. C est la constante de la loi des aires. 18-1-2 Utilisation du théorème du moment cinétique On arrive aux mêmes conclusions par le raisonnement suivant : Si le mouvement de M est à accélération centrale, de centre O, M est soumis à la force totale F m a // OM , c'est-à-dire à une force centrale (exercée par O). Le moment en O de la force est O OM F 0 . d LO Le théorème du moment cinétique appliqué en O (fixe) donne O 0 donc le moment dt cinétique en O, L O OM m v = m C est donc constant. 18-1-3 Formules de Binet On utilisera les coordonnées cylindriques de M (r,,z = 0) avec Oz dans la direction et dans le sens de C. C L On a donc C C e z OM v r u r r e r r e r 2 e z constant donc 2 = O2 . r mr Pour simplifier les expressions, on posera u 1 du d2u , u' et u ' ' 2 . On a donc Cu 2 r d d u u' On a donc r 2 2 = – Cu' donc v Cu' e r Cu e . u u 2 2 2 2 D'où la première formule de Binet : v C u u' . En dérivant la vitesse on obtient a Cu' ' e r Cu e r les termes en e s'éliminent car a // OM . 2 2 D'où la deuxième formule de Binet : a C u u u ' ' e r . 18-2 Cas d'une force centrale conservative du type F Fr (r ) e r 18-2-1 Énergie potentielle, conservation de l'énergie mécanique Dans ce cas, le travail élémentaire de la force s'écrit W = F d M Fr (r ) e r . dr e r rd e F(r )dr et W = – dEp = Fr(r) dr donc l'énergie potentielle n'est fonction que de r . La constante d'intégration est toujours choisie pour que lim Ep 0 . r L'énergie mécanique de M est E = Ep(r) + 1 mv 2 , elle est constante. 2 18-2-2 Énergie potentielle effective, énergie cinétique radiale 2 2 La vitesse de M est v r e r r e et son carré est v 2 r r 2 avec C L0 = donc r 2 mr 2 2 C2 1 2 mC 2 E mr Ep (r ) , elle est la somme de deux donc l'énergie mécanique de M est 2 r2 2r 2 termes : l'un qui ne dépend que de r, comme Ep(r) et que l'on appelle "énergie potentielle effective" et l'autre v2 r qui serait l'énergie cinétique si la vitesse était radiale (// OM ) que l'on appelle "énergie cinétique radiale". Énergie cinétique radiale : Ec rad 1 2 m r . On a donc Ecrad 0 . 2 2 L mC 2 Ep (r ) O 2 . Énergie potentielle effective : Ep eff Ep (r ) 2 2r 2mr Énergie mécanique : E Ec rad Ep eff . On a donc Ep eff E 18-2-3 Différents types de mouvements La condition Ep eff E , si l'on connaît l'expression de Epeff en fonction de r, permet de déterminer le type de mouvement de M suivant la valeur de l'énergie mécanique (constante), donc suivant la valeur initiale de E, et suivant la valeur initiale de r : On a de toute façon lim Ep eff 0 et, en général lim Ep eff . r r 0 Supposons par exemple que Epeff (r) ait l'allure ci-dessous. Epeff État de diffusion E1 E2 État lié État de diffusion 0 r E3 État lié E0 Pour E = E1, r [r1 , ] , M peut s'éloigner indéfiniment de O, il n'est pas lié à O. Pour E = E2, deux cas sont possibles suivant la valeur initiale de r : r [r2m , r2M ] si initialement r est dans cet intervalle, M est lié à O, il reste à une distance finie de O. r [r2 , ] si initialement r r2, M n'est pas lié à O. Pour E = E3, r [r3m , r3M ] , M est lié à O. Pour E = E0, r = r0, M est lié )à O et a un mouvement circulaire autour de O. Si M peut s'éloigner indéfiniment de O, on parle d'état de diffusion. Si M reste à une distance finie de O, on parle d'état lié. Bien entendu, un état lié n'est possible que si la force exercée par O sur M est attractive. 18-2-4 Obtention de l'équation de la trajectoire en coordonnées polaires On peut utiliser la deuxième loi de Newton F Fr (r ) e r = m a , et la deuxième formule de Binet. 1 Fr étant une fonction de r est aussi une fonction de u = , donc u en fonction de est solution de r 2 L l'équation différentielle Fr (u) mC 2u 2 u u' ' ou Fr (u ) 0 u 2 u u ' ' 0 . m La constante C ou la constante L0 est déterminée avec les conditions initiales. 1 : interaction gravitationnelle, interaction électrostatique r2 18-3-1 Expression de l'énergie potentielle, potentiel électrostatique, potentiel gravitationnel Si M de masse m est attiré par la masse m0 placée en O fixe, M subit la force d'attraction m m m m gravitationnelle F G O 3 OM G O2 e , son travail élémentaire est W = – dEp = Fr dr donc r OM r m m m m dEp G O2 dr et, avec lim Ep 0 , Ep G O . r r r m Le potentiel gravitationnel en M est V, défini par Ep = m V donc V G O . r 18-3 Cas des forces centrales en Si M de charge électrique q est attiré ou repoussé par la charge qO placée en O fixe, M subit la force qOq qOq électrostatique F OM e , son travail élémentaire est W = – dEp = Fr dr donc 40 OM 3 40 r 2 r dEp q q qOq dr et, avec lim Ep 0 , Ep O . 2 r 40 r 40 r qO . 40 r Dans les deux cas, la force est centrale et inversement proportionnelle au carré de la distance au K K centre, l'énergie potentielle est de la forme Ep et on a Fr 2 avec : r r q q K G m 0 m pour une interaction gravitationnelle et K O pour une interaction électrostatique. 40 K > 0 pour une force de répulsion électrostatique entre deux charges de même signe. K < 0 pour une force d'attraction électrostatique entre deux charges de signes opposés ou pour une force d'attraction gravitationnelle. Le potentiel électrostatique en M est V, défini par Ep = q V donc V 18-3-2 Énergie potentielle effective, différents types de mouvements 2 K LO K mC 2 Dans ces deux cas, on a donc Ep eff . r 2mr 2 r 2r 2 Si K > 0 : Epeff décroît de à 0 quand r croît de 0 à . Il n'y a que des états de diffusion. Epeff r [ r1 , ] E1 r1 r mC 2 dEp eff K mC 2 r 2 3 0 pour r = 0 Si K < 0 : Epeff passe par un minimum négatif car , K dr r r K2 mC 2 r0 r . alors Epeff = E 0 . On remarque aussi que Ep = 0 pour eff 2mC 2 2K 2 Il y a donc différents cas : Si E > 0 : états de diffusion. Si E < 0 : états liés, avec le cas particulier E = E0 pour lequel le mouvement de M est circulaire, de rayon r0. Epeff r [ r1 , ] E1 0 E2 r1 rm r0 r0 2 r [ rm , rM ] rM r E0 18-3-3 Équation de la trajectoire en coordonnées polaires Elle est donnée par l'équation différentielle Fr (u) mC 2u 2 u u' ' . K K Avec Fr 2 Ku 2 l'équation différentielle s'écrit : u ' ' u et sa solution générale est de la mC 2 r K A cos( 0 ) (avec le choix de 0 tel que A soit positif) d'où : forme u mC 2 mC 2 1 1 K r . K u AmC 2 A cos( 0 ) 1 cos( 0 ) mC 2 K Cas d'une force attractive p Pour une force attractive, K < 0 , on a affaire à une conique d'équation r avec : 1 e cos( 0 ) AmC 2 mC 2 , et l'excentricité est e , (p et e sont > 0). K K Si e = 0 : cercle. Si e ] 0;1[ : ellipse. Si e = 1 : parabole. Si e > 1 : branche d'hyperbole. le cercle et les ellipses correspondent aux états liés, la parabole et les branches d'hyperbole correspondent aux états de diffusion. La parabole correspond au cas limite. le paramètre est p B A M a O' b c a p p x O P 0 x 0 O P Dans le cas d'une branche d'hyperbole, il s'agit de celle pour laquelle O est du côté de sa concavité. (On le démontre en tenant compte de r > 0). O' p M 0 P x O Cas d'une force répulsive Pour une force répulsive, K > 0 , il ne peut y avoir que des états de diffusion et la trajectoire ne peut être qu'une branche d'hyperbole puisque le cas limite de la parabole n'existe pas. p AmC 2 mC 2 On a donc e et p , l'équation de la trajectoire s'écrit r . 1 e cos( 0 ) K K La branche d'hyperbole décrite par M est celle pour laquelle O est du côté de sa convexité. (On le démontre en tenant compte de r > 0). O' P 0 x O Dans tous les cas :le paramètre est p mC 2 K et l'excentricité est e AmC 2 . K 18-3-4 Énergie mécanique K v2 mC 2 2 m Ku u u'2 E = Ep + Ec = r 2 2 1 e cos( 0 ) e sin( 0 ) Si K < 0 : mC2 = – Kp , u et u ' donc p p K K 2 2 E 2 2e cos( 0 ) 1 e cos( 0 ) e sin( 0 ) 1 e2 2p 2p 1 e cos( 0 ) e sin( 0 ) Si K > 0 : mC2 = Kp , u et u ' donc p p K K K 2 2 E 2 2e cos( 0 ) 1 e cos( 0 ) e sin( 0 ) 1 e2 1 e2 . 2p 2p 2p Dans tous les cas : E e 2p K 2 1 . Pour une trajectoire circulaire ou elliptique, donc pour un état lié : e < 1 donc E < 0 . Pour une trajectoire parabolique : e = 1 donc E = 0 . Pour une trajectoire hyperbolique : e > 1 donc E > 0 . 18-4 Attraction gravitationnelle par un astre 18-4-1 Cas général Si l'astre attracteur a sa masse mO répartie suivant une symétrie sphérique de centre O, on démontre avec le théorème de Gauss (voir cours d'électrostatique) que la force d'attraction qu'il exerce sur le point matériel M est la même que si toute la masse mO se trouvait en O. On supposera que les forces exercées par les autres astres sur M sont négligeables devant celle qu'exerce O et que le repère d'origine O dont les axes sont orientés vers des étoiles lointaines constitue un référentiel galiléen. On a donc K G m O m . C2 p AC 2 avec p et e G mO 1 e cos( 0 ) G mO constantes A et C sont déterminées par les conditions initiales sur la position et sur la vitesse. G m O m (e 2 1) G 2 m O 2 m (e 2 1) . L'énergie mécanique de M est E 2p 2C 2 G m O m1 e cos( 0 ) L'énergie potentielle est Ep . p G m O m e 2 2e cos( ) 1 L'énergie cinétique est Ec E Ep 0 2p r M décrit une conique d'équation . Les 18-4-2 Trajectoire circulaire Dans ce cas e = 0 (A = 0) et r = p = r0 est constant. Si l'on note v 0 la vitesse initiale, on a v OM donc C = r0 v0 = r0 v donc v = v0 est constante, le mouvement est uniforme. 2 2 r0 v 0 On a donc r0 . Pour que le mouvement soit circulaire, il faut que v 0 OM 0 et que G mO v0 mOG . r0 Par exemple, pour un satellite artificiel sur une orbite basse, r0 R T 6,37.10 6 m (rayon terrestre), avec G = 6,67.1011 N.m2.kg–2 et m0 = MT 5,97.10 24 kg on obtient v0 = 7,9 km.s–1. C'est la première vitesse cosmique : v I MTG 7,9 km.s 1 . RT L'énergie mécanique est E G mO m G mO m , l'énergie potentielle est Ep et l'énergie 2r0 r0 G mO m . On a donc Ep = 2 E et E = – Ec. Il en résulte que pour un satellite, l'atmosphère 2r0 (raréfiée) dans laquelle il est plongé diminuant par frottement son énergie mécanique, sa distance r0 au centre de la Terre diminue, il perd de l'altitude, mais sa vitesse croît car Ec = – E croît. cinétique Ec 3 r0 m 0G 2r0 r0 La période de révolution est T donc 2 . 2r0 T 4π 2 v0 m OG 18-4-3 Trajectoires elliptiques Voir le dessin de l'ellipse du 18-3-3. P est le péricentre (périgée, périhélie, périastre suivant l'attracteur) et A est l'apocentre (apogée, aphélie ou apoastre suivant l'attracteur). Le grand axe d'une ellipse est 2 a = PO + OA = PO + PO' = BO + BO' = MO + MO' = PO + PO' car l'ellipse est l'ensemble de points d'un plan dont la somme des distances aux deux foyers (O et O') est constante. p p OP = r pour = 0 donc OP = et OA = r pour = 0 + donc OA . 1 e 1 e p 1 2p 1 2a = p donc a 2 1 e2 1 e 1 e 1 e c O' P OP OA OP p 1 1 pe e ae donc l'excentricité est . a 2 2 2 1 e 1 e 1 e2 p . On a donc aussi b2 = pa . b a 2 c2 a 1 e2 2 1 e c O L'aire de la surface de l'ellipse est S = ab . Donc S = a2 1 e 2 . L'énergie mécanique de M sur une trajectoire elliptique est E La vitesse aréolaire est constante et vaut (en norme) Donc a 2 1 e 2 T G m 0 a (1 e 2 ) 2 G G mO m mOm 2 (e 1) soit E . 2a 2p dS S C C2 avec p = a (1 – e2). dt T 2 G m0 . a 3 mOG : T2 4 2 le cube du demi grand axe de l'orbite d'une planète est proportionnel au carré de sa période de révolution. La première loi de Kepler affirme que les orbites sont des ellipses dont le Soleil est un foyer et la deuxième est la loi des aires. Après simplification, en élevant au carré, on obtient la troisième loi de Kepler 18-4-4 Trajectoire parabolique, vitesse de libération p Si la trajectoire est parabolique, e = 1 et r . 1 cos( 0 ) p . 2 G m O m1 cos( 0 ) L'énergie mécanique est E = 0 donc Ep = – Ec = Ep . p Lorsque r , Ep 0 et E = 0 donc Ec 0 . Alors que pour une trajectoire hyperbolique la vitesse ne tend pas vers 0. mv 2 K G mOm On a donc . Pour un vaisseau spatial se trouvant prés de la Terre la vitesse 2 r r nécessaire pour avoir une trajectoire parabolique est la vitesse de libération ou seconde vitesse cosmique : La distance minimale d'approche est atteinte au péricentre : OP v II 2G m 0 = vI 2 = 11,2 km.s–1. RT