Cours de 4ème

Cours de 4ème – M. ARDHUIN – Collège Fénelon à Cambrai
1 | P a g e
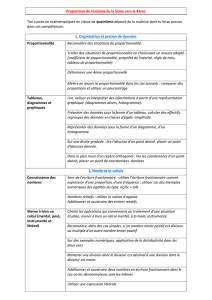
Chapitre G1 : Transformations de figures
1/ Rappels : symétrie axiale et symétrie centrale
2/ Transformer une figure par translation
3/ Transformer une figure par rotation
4/ Frises, pavages et rosaces
1/ Rappels : symétrie axiale et symétrie centrale
a/ La symétrie axiale
b/ La symétrie centrale

Cours de 4ème – M. ARDHUIN – Collège Fénelon à Cambrai
2 | P a g e
2/ Transformer une figure par translation
a/ Définition
b/ Propriété
3/ Transformer une figure par rotation
a/ Définition
b/ Propriété
La figure F2 est obtenue à partir de la figure F1
par un glissement rectiligne qui amène A en A’.
On dit que La figure F2 est l’image de la figure F1
par la translation qui transforme A en A’.

Cours de 4ème – M. ARDHUIN – Collège Fénelon à Cambrai
3 | P a g e
4/ Frises, pavages et rosaces

Cours de 4ème – M. ARDHUIN – Collège Fénelon à Cambrai
4 | P a g e
Chapitre G2 : Triangles égaux
1/ Triangles égaux
2/ Cas d'égalité des triangles
1/ Triangles égaux
Définition : Des triangles égaux sont des triangles qui ont des côtés deux à deux de
même longueur.
Remarque : Des triangles égaux sont superposables et, par conséquent, ont des angles deux
à deux égaux.
2/ Cas d'égalité des triangles

Cours de 4ème – M. ARDHUIN – Collège Fénelon à Cambrai
5 | P a g e
Chapitre G3 : L’égalité de Pythagore
1/ L’égalité de Pythagore
a/ Hypoténuse d’un triangle rectangle
b/ Propriété : le théorème de Pythagore
c/ Conséquence
d/ Application pratique
2/ Comment savoir si un triangle est rectangle ?
1/ L’égalité de Pythagore
a/ Hypoténuse d’un triangle rectangle
Dans un triangle rectangle, l’hypoténuse est le côté opposé à l’angle droit.
b/ Propriété (Théorème de Pythagore)
Si un triangle est rectangle, alors le carré de l’hypoténuse est égal à la somme des carrés
des deux autres côtés.
BC² = AB² + AC²
Egalité de Pythagore
c/ Conséquence
Dans un triangle rectangle, l’hypoténuse est le plus long côté.
d/ Application pratique
L’égalité de Pythagore permet, dès que l’on connaît les longueurs de deux des côtés d’un
triangle rectangle, de calculer la longueur du troisième.
Exemples :
Notez bien : Pour déterminer le nombre positif dont on connaît le carré, on utilise la touche
(racine carrée) d’une calculatrice.
A
B
C
Hypoténuse