fonctions usuelles - Gérard Lavau

© 2013 - Gérard Lavau - http://lavau.pagesperso-orange.fr/index.htm
Vous avez toute liberté pour télécharger, imprimer, photocopier ce cours et le diffuser gratuitement. Toute diffusion à
titre onéreux ou utilisation commerciale est interdite sans accord de l'auteur.
Si vous êtes le gestionnaire d'un site sur Internet, vous avez le droit de créer un lien de votre site vers mon site, à
condition que ce lien soit accessible librement et gratuitement. Vous ne pouvez pas télécharger les fichiers de mon site
pour les installer sur le vôtre.
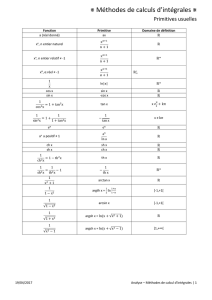
FONCTIONS USUELLES
PLAN
I : Fonctions exponentielles
1) Exponentielles et logarithmes
2) Fonctions trigonométriques hyperboliques
II : Fonctions circulaires
1) Fonctions trigonométriques
2) Réciproque des fonctions trigonométriques
Annexe : trigonométrie
I : Fonctions exponentielles
1– Exponentielles et logarithmes
1
❑ ln(x) est la primitive de définie sur ]0, +∞[ et s'annulant en x = 1. Autrement dit :
x
x
1
ln(x) = ⌠
 t dt
⌡
1
1
Sa dérivée étant strictement positive, ln est donc strictement croissante. La dérivée de ln(ax) valant
x
a 1
= , ln(ax) est égal à ln(x) + Cte. La valeur de Cte est obtenue en prenant x = 1, ce qui donne la
ax x
relation célèbre :
ln(ax) = ln(x) + ln(a)
Cette relation, transformant produit en somme, a permis, depuis le XVIIème et jusqu'à l'introduction
des calculatrices à bas prix vers 1980, d'accélérer notablement les possibilités de calcul des
mathématiciens. Ainsi Laplace s'émerveille-t-il "des logarithmes, admirable instrument, qui, en
réduisant à quelques heures le travail de plusieurs mois, double si l'on peut dire la vie des
astronomes, et leur épargne les erreurs et les dégoûts inséparables des longs calculs". En prenant
1
a = , on obtient :
x
1
ln( ) = – ln(x)
x
Etant strictement croissante, ou bien
lim ln(x) = +∞ ou bien lim ln(x) = l limite finie.
x → +∞
x → +∞
n
Comme, pour n entier, ln(2 ) = nln(2) (récurrence facile) et que cette quantité tend vers +∞ quand n
tend vers +∞, la seule conclusion possible est :
lim ln(x) = +∞
x → +∞
1
Et donc, en considérant :
x
-1-
lim ln(x) = –∞
x→0
ln réalise donc une bijection de ]0, +∞[ sur ]–∞, +∞[. Sa réciproque est l'exponentielle :
t = ln(x) ⇔ x = et
e
1
Le nombre e est tel que 1 = ln(e) soit ⌠
 t dt = 1. e vaut environ 2,71828...
⌡1
Les limites relatives à ln se traduisent pour l'exponentielle de la façon suivante :
lim ex = +∞
x → +∞
lim ex = 0
x → –∞
La règle de dérivation d'une fonction réciproque (cf le chapitre Dérivation dans le fichier
DERIVEE.PDF) conduit à :
(ex)' = ex
x+y
x y
On a également e = e e puisqu'en prenant les logarithmes des deux membres, on obtient d'une
part :
ln(ex+y) = x + y
et d'autre part :
ln(ex ey) = ln(ex) + ln(ey) = x + y
❑ Pour tout a strictement positif et b, on posera ab = eln(a)b. Cette définition est compatible avec le
calcul des puissances de a, puisque, pour n entier, on a :
eln(a)n = eln(a) + ln(a) + ... + ln(a) avec n exposant ln(a)
= eln(a) × eln(a) × ... × eln(a)
= a × a × ... × a
= an
On a alors ln(ab) = b ln(a), et également (ex)y = exy obtenu en prenant a = ex et b = y dans la formule
donnant ab. On a enfin, pour a > 0 et différent de 1 :
ln(x)
x = at ⇔ x = eln(a)t ⇔ ln(x) = ln(a)t ⇔ t =
ln(a)
ln(x)
at est l'exponentielle de t en base a et
est le logarithme de x en base a. Le logarithme le plus
ln(a)
utilisé en dehors du logarithme en base e (dit népérien) est le logarithme décimal, pour lequel a = 10,
et que l'on note souvent log10, voire même log. On rencontre aussi en informatique le logarithme en
base 2.
Si u est une fonction strictement positive, et v une fonction quelconque, on a :
u(x)v(x) = ev(x) ln(u(x))
La deuxième forme peut servir à dériver la fonction ou à en calculer les limites.
❑ Un certain nombre de limites usuelles doivent être connues :
ln(x)
ln(x)
(i) lim
= 0 et plus généralement lim
a = 0 pour tout a > 0
x → +∞ x
x → +∞ x
(ii) lim xln(x) = 0 et plus généralement lim xaln(x) = 0
x→0
x→0
x
e
ex
(iii) lim
= +∞ et plus généralement lim
a = +∞ pour tout a > 0
x → +∞ x
x → +∞ x
-2-
lim xex = 0 et plus généralement lim xaex = 0 pour tout a > 0
x → –∞
x → –∞
ln(x)
1 – ln(x)
Montrons (i). Soit f(x) =
. f admet pour dérivée f '(x) =
qui est négative pour x > e,
x
x2
donc f est décroissante strictement positive sur [e, +∞[. Elle admet donc une limite l positive ou nulle
ln(y)
en +∞. Cette limite est aussi celle de
avec y = x2, soit :
y
ln(x2)
=l
lim
2
x → +∞ x
2ln(x)
⇒
lim
=l
2
x → +∞ x
ln(x) 1
⇒
lim 2 ×
× =l
x
x
x → +∞
⇒
2×l×0=l
⇒
l=0
(iii)
Toutes les autres limites s'en déduisent. En remplaçant x par xa, on obtient :
ln(xa)
aln(x)
ln(x)
0 = lim
= lim
⇒ lim
a
a
a = 0
x
x
x → +∞
x → +∞
x → +∞ x
(ii) En changeant dans (i) x en 1/x avec x tendant vers 0, on obtient :
ln(1/x)
0 = lim
= lim – xln(x) ⇒ lim xln(x) = 0
x → 0 1/x
x→0
x→0
En remplaçant x par xa, on obtient lim xaln(x) = 0
x→0
x
ex
(iii) En changeant dans (i) x par ex, on obtient lim
lim
= +∞. En élevant à la
x = 0 ou
x → +∞ e
x → +∞ x
eax
eax
a
puissance a, on obtient lim
=
+∞
⇒
lim
a
a a = +∞ en divisant par a et enfin, en
x
a
x
x → +∞
x → +∞
ex
remplaçant ax par x, on obtient bien lim
a = +∞.
x → +∞ x
(iv) Remplacer x par –x dans (iii).
2– Fonctions trigonométriques hyperboliques
a) sh(x) et ch(x) :
On pose :
ex – e–x
––
2
(sinus hyperbolique)
ex + e–x
2
(cosinus hyperbolique)
sh(x) =
ch(x) =
On vérifie facilement que :
ex = sh(x) + ch(x)
sh est impair.
ch est pair et strictement positif.
(sh et ch sont respectivement la partie paire et impaire de l'exponentielle)
sh' = ch donc sh est strictement croissante, et du signe de x.
ch' = sh donc ch est décroissant sur ]–∞,0] et croissant sur [0,+∞[.
-3-
sh(x) ∼ ch(x) ∼
(La notation
ex
au voisinage de +∞.
2
∼
est définie dans le chapitre Limites et Continuité qu'on trouvera dans le fichier
f(x)
LIMITES.PDF. f ∼ g au voisinage de x0 signifie que lim
= 1)
g(x)
x → x0
sh(x) ∼ x au voisinage de 0 (car sh'(0) = 1).
ch(x) ∼ 1 au voisinage de 0.
x2
x
ch(x) – 1 ∼ car on vérifiera que ch(x) – 1 = 2 sh2( )
2
2
Il existe des formules de trigonométries hyperboliques, en particulier :
ch2(x) – sh2(x) = 1
On consultera sur ce point l'annexe, donnant une comparaison des formules de trigonométries
circulaires et hyperboliques.
y
ch
sh
o
x
sh étant continue strictement monotone de
sur , elle admet donc une réciproque qu'on peut
calculer explicitement :
ey – e–y
x = sh(y) =
2
2y
y
⇔
e – 2e x – 1 = 0
⇔
ey = x ± x2+1
La seule racine positive est x + x2 + 1 . On a donc :
y = ln(x + x2 + 1)
-4-
On vérifiera que sa dérivée vaut
de
1
. En calcul intégral, on pourra donc utiliser comme primitive
x +1
2
1
la fonction ln(x + x2 + 1).
x +1
2
De même, ch étant continue strictement monotone de [0,+∞[ sur [1,+∞[, elle admet une réciproque :
ey + e–y
x = chy =
et y ≥ 0
2
⇔
e2y – 2eyx + 1 = 0
⇔
ey = x ± x2 – 1
Les deux racines sont positives, mais la seule racine supérieure ou égale à 1 est x + x2 – 1. On a
donc :
y = ln(x + x2 – 1)
En fait, il peut être parfois utile d'étendre cette fonction à l'intervalle ]–∞,–1] en considérant
1
ln x + x2 – 1 , dont on vérifiera en exercice qu'elle est impaire. Sa dérivée vaut 2
. Ainsi, en
x –1
1
calcul intégral, on pourra utiliser comme primitive de 2
la fonction ln x + x2 – 1 .
x –1
b) th(x) :
th(x) =
sh(x) ex – e–x e2x – 1
=
=
ch(x) ex + e–x e2x + 1
(tangente hyperbolique)
On a :
th est impaire.
1
th'(x) = 2 = 1 – th2(x) > 0 donc th est strictement croissante.
ch (x)
lim th(x) = 1 et lim th(x) = –1
x→+∞
x→–∞
th(x) ∼ x au voisinage de 0 (car th'(0) = 1).
-5-
y
th
o
th est continue strictement monotone de
e2y – 1
x = th(y) = 2y
e +1
x
+
1
⇔
e2y =
1–x
1 x+1
⇔
y = ln
.
2 1–x
x
sur ]–1,1[. Elle admet donc une réciproque :
Il est parfois utile d'étendre cette fonction à
– {–1,1} en considérant
1
x+1
ln
. Sa dérivée vaut
2
1–x
1
.
1 – x2
II : Fonctions circulaires
1– fonctions trigonométriques
J'ose espérer qu'aucun lecteur n'ignore ce que sont les fonctions sinus, cosinus et tangente. Il
convient d'apprendre les formules trigonométriques situées en fin de ce chapitre .
2– Réciproque des fonctions trigonométriques
a) arcsin :
sin : [– π, π] → [–1,1] est continue strictement monotone. Elle admet donc une réciproque notée
2 2
arcsin. On a donc :
θ = arcsin(x) ⇔ θ ∈ [– π, π] et x = sin(θ)
2 2
-6-
(On fera un rapprochement dans la formulation avec l'équivalence :
y = x ⇔ y ≥ 0 et x = y2)
Voici un tableau de valeurs :
x
–1
3
2
–
–
2
2
arcsin(x)
–π
–π
–π
2
3
4
1
2
0
1
2
–π
6
0
π
6
–
2
2
π
4
3
2
π
3
1
sinθ
π
2
θ
arcsin est strictement croissante, impaire :
❑ arcsin(–x) = – arcsin(x)
❑ ∀ x ∈ [–1,1], sin(arcsin(x)) = x
❑ ∀ θ ∈ [–π/2,π/2], arcsin(sin(θ)) = θ
MAIS cette dernière relation est fausse si θ appartient à un autre intervalle.
2 π
)=
4
2
(On fera un rapprochement dans la formulation des relations précédentes avec :
∀ x ∈ +, ( x)2 = x
EXEMPLE : arcsin(sin(3π/4)) = arcsin(
∀y∈
+
, y2 = y
MAIS pour y quelconque dans
, y2 = y
❑ cos(arcsin(x)) = 1 – x2
car cos est positif sur [– π, π], et dans ce cas, cos(θ) = 1 – sin2(θ)
2 2
1
(voir le chapitre Dérivation dans le fichier DERIVEE.PDF pour
1 – x2
savoir comment dériver la réciproque d'une fonction).
La dérivée d'arcsin(x) est
-7-
y
arcsinus
sinus
o
x
b) arccos :
cos : [0, π] → [–1, 1] est continue strictement monotone. Elle admet donc une réciproque notée
arccos. On a donc :
θ = arccos(x) ⇔ θ ∈ [0, π] et x = cos(θ)
Voici un tableau de valeurs :
x
–1
3
2
–
–
2
2
arccos(x)
π
5π
3π
6
4
1
2
0
1
2
2π
3
π
2
π
3
–
2
2
π
4
arccos est strictement décroissante :
❑
arccos(–x) = π – arccos(x)
En effet, θ = arccos(–x) ⇔ –x = cos(θ) et θ ∈ [0, π]
⇔ x = –cos(θ) = cos(π – θ) et π–θ ∈ [0, π]
⇔ π – θ = arccos(x)
❑ ∀ x ∈ [–1, 1], cos(arccos(x)) = x
❑ ∀ θ ∈ [0, π], arccos(cosθ) = θ
MAIS cette dernière relation est fausse si θ appartient à un autre intervalle.
2
EXEMPLE : arccos(cos(– π)) = arccos( ) = π
2
4
4
❑ sin(arccos(x)) = 1 – x2
car sin est positif sur [0, π], et dans ce cas, sin(θ) = 1 – cos2(θ)
-8-
3
2
π
6
1
cosθ
0
θ
π
2
❑ arcsin(x) + arccos(x) =
π π
En effet, θ = arcsin(x) ⇔ θ ∈ [– , ] et sin(θ) = x
2 2
π
π
⇔ x = cos( – θ) et – θ ∈ [0,π]
2
2
π
⇔ – θ = arccos(x)
2
La dérivée de arccos(x) est –
1
1 – x2
y
arccosinus
o
x
cosinus
c) arctan :
tan : ]– π, π[ →
2 2
On a donc :
est continue strictement monotone. Elle admet donc une réciproque notée arctan.
θ = arctan(x) ⇔ θ ∈ ]– π, π[ et x = tan(θ)
2 2
Voici un tableau de valeurs :
x
–∞
– 3
–1
–π
2
–π
4
arctan(x)
–π
3
1
3
–π
6
–
0
0
arctan est strictement croissante, impaire :
-9-
1
3
π
6
1
π
4
3
π
3
+∞
tanθ
π
2
θ
❑ arctan(–x) = – arctan(x)
❑ ∀ x ∈ , tan(arctan(x)) = x
❑ ∀ θ ∈ ]–π/2,π/2[, arctan(tan(θ)) = θ
MAIS cette dernière relation est fausse si θ appartient à un autre intervalle.
Exemple : arctan[tan(3π/4)] = arctan(–1) = – π
4
1
1 + x2
1
car cos est positif sur [– π, π], et dans ce cas, cos(θ) =
2 2
1+tan2(θ)
x
❑ sin(arctan(x)) =
1 + x2
❑ cos(arctan(x)) =
1
❑ arctan(x) + arctan( ) = π sgn(x) où sgn(x) = 1 si x > 0
x 2
= –1 si x < 0
Les deux membres étant des fonctions impaires de x, il suffit de le montrer pour x > 0. Dans ce cas,
on a :
1
1
π
θ = arctan( ) ⇔ = tan(θ) et θ ∈ ]0, [
x
2
x
1
⇔x=
= tan(π – θ) et π – θ ∈ ]0, π[
2
2
2
tan(θ)
π
⇔ – θ = arctan(x)
2
1
La dérivée d'arctan(x) est
.
1 + x2
- 10 -
y
tan
arctan
o
x
- 11 -
Annexe : trigonométrie
eix + e–ix
2
ix
e – e–ix
sin(x) =
2i
sin(x)
tan(x) =
cos(x)
ex + e–x
2
x
e – e–x
sh(x) =
2
sh(x)
th(x) =
ch(x)
cos(x) =
ch(x) =
FORMULES
2
2
cos (x) + sin (x) = 1
cos(a+b) = cos(a) cos(b) – sin(a) sin(b)
cos(a–b) = cos(a) cos(b) + sin(a) sin(b)
cos(2x) = cos2(x) – sin2(x)
1 + cos(2x)
cos2(x) =
2
sin(a+b) = sin(a) cos(b) + cos(a) sin(b)
sin(a–b) = sin(a) cos(b) – cos(a) sin(b)
sin(2x) = 2 sin(x) cos(x)
1 – cos(2x)
sin2(x) =
2
tan(a) + tan(b)
tan(a + b) =
1 – tan(a) tan(b)
tan(a) – tan(b)
tan(a – b) =
1 + tan(a) tan(b)
2 tan(x)
tan(2x) =
1 – tan2(x)
1
cos(a) cos(b) = [cos(a + b) + cos(a – b)]
2
1
sin(a) sin(b) = – [cos(a + b) – cos(a – b)]
2
1
sin(a) cos(b) = [sin(a + b) + sin(a – b)]
2
p+q
p–q
cos(p) + cos(q) = 2 cos
cos
2
2
p+q
p–q
cos(p) – cos(q) = – 2 sin
sin
2
2
p+q
p–q
sin(p) + sin(q) = 2 sin
cos
2
2
ch2(x) – sh2(x) = 1
ch(a+b) = ch(a) ch(b) + sh(a) sh(b)
ch(a–b) = ch(a) ch(b) – sh(a) sh(b)
ch(2x) = ch2(x) + sh2(x)
1 + ch(2x)
ch2(x) =
2
sh(a+b) = sh(a) ch(b) + ch(a) sh(b)
sh(a–b) = sh(a) ch(b) – ch(a) sh(b)
sh(2x) = 2 sh(x) ch(x)
ch(2x) – 1
sh2(x) =
2
th(a) + th(b)
th(a + b) =
1 + th(a) th(b)
th(a) – th(b)
th(a – b) =
1 – th(a) th(b)
2 th(x)
th(2x) =
1 + th2(x)
1
ch(a) ch(b) = [ch(a + b) + ch(a – b)]
2
1
sh(a) sh(b) = [ch(a + b) – ch(a – b)]
2
1
sh(a) ch(b) = [sh(a + b) + sh(a – b)]
2
p+q p–q
ch(p) + ch(q) = 2 ch
ch
2
2
p+q p–q
ch(p) – ch(q) = 2 sh
sh
2
2
p+q p–q
sh(p) + sh(q) = 2 sh
ch
2
2
x
pour t = tan( )
2
2t
sin(x) =
1 + t2
1 – t2
cos(x) =
1 + t2
2t
tan(x) =
1 – t2
x
pour t = th( )
2
2t
sh(x) =
1 – t2
1 + t2
ch(x) =
1 – t2
2t
th(x) =
1 + t2
- 12 -
DERIVEES
ch'(x) = sh(x)
sh'(x) = ch(x)
1
th'(x) = 2
= 1 – th2(x)
ch (x)
cos'(x) = –sin(x)
sin'(x) = cos(x)
1
tan'(x) =
= 1 + tan2(x)
cos2(x)
PARAMETRAGES
2
2
x
y
+
=1
a2 b2
y = b sin(t)
x2 y2
–
=1
a2 b2
y = b sh(t)
paramétrage de l'ellipse
paramétrage de l'hyperbole
x = a cos(t)
x = a ch(t)
EQUIVALENTS au voisinage de 0
sin(x) ~ x
cos(x) ~ 1
tan(x) ~ x
sh(x) ~ x
ch(x) ~ 1
th(x) ~ x
1 – cos(x) ∼ x
2
ch(x) – 1 ∼ x
2
2
2
DEVELOPPEMENTS LIMITES au voisinage de 0
n
sin(x) = ∑ (–1)k
k=0
n
x2k+1
+ o(x2n+2)
(2k+1)!
sh(x) = ∑
x2k
+ o(x2n+1)
(2k)!
ch(x) = ∑
cos(x) = ∑ (–1)k
k=0
n
k=0
n
k=0
◆
- 13 -
x2k+1
+ o(x2n+2)
(2k+1)!
x2k
+ o(x2n+1)
(2k)!