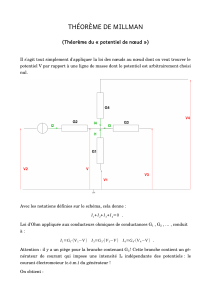
résumé de cours

Nombres réels
I — Ensembles de nombres
Définition 1.1 — On appelle R l’ensemble des nombres rationnels Q auquel on
adjoint toutes les limites des suites convergentes de rationnels.
II — Les opérations usuelles
Proposition 2.1 — Propriétés de l’addition et de la multiplication
– elle sont associatives ( et peuvent donc être notée sans parenthèses)
∀(x,y,z)∈R3,(x+y) + z=x+ ( y+z)
et (x y)z=x(yz)
– elle sont commutatives
∀(x,y)∈R2,x+y=y+xet x y =y x
– elles possèdent chacune un élément neutre
∀x∈R,x+0=xet ∀x∈R,x×1=x
– chaque élément de Rpossède un opposé
∀x∈R,∃x0∈R,x+x0=0
(cet opposé est unique, il est noté −x) ;
– chaque élément de R∗possède un inverse
∀x∈R∗,∃x∗∈R,x×x∗=1
(cet inverse est unique, il est noté 1/x) ;
– la multiplication est distributive sur l’addition
∀(a,x,y)∈R3,a×(x+y) = a×x+a×y
Définition 2.2 — Puissances entières positives
Par définition on note
∀n∈N,∀x∈N,xn=1×x×x×···× x
| {z }
nfois
Théorème 2.3 — Propriété caractéristique de la notation puissance
∀x∈R,∀(n,m)∈N2xnxm=xn+m
Propriété 2.4 —
1) Pour x∈Ret (n,m)∈N2(xn)m=xnm = (xm)n.
2) Pour (x,y)∈R2et n∈N(x y)n=xnyn.
Définition 2.5 — Puissances entières négatives
Soit x∈R∗et n∈N∗. Par définition on note x−1=1/xet x−n= (x−1)n

III — Relation d’ordre 2
Théorème 2.6 — Propriété caractéristique de la notation puissance
Pour (x,y)∈(R∗)2et (n,m)∈Z2on a
xn+m=xnxm(xn)m=xnm (x y)n=xnyn
III — Relation d’ordre
Proposition 3.1 — Propriété de la relation d’ordre dans R
Soit (a,b,c,d)∈R4.
1) si a¶bet c¶dalors a+c¶b+d(addition terme à terme) ;
2) si a¶bet 0¶calors ac ¶bc.
3) si a¶bet c¶0alors bc ¶ac.
4) si 0¶a¶b et 0¶c¶d alors 0¶ac ¶bd (multiplication terme à
terme d’inégalités positives).
5) 0¶a¶b=⇒a2¶b2(croissance de x7→ x2sur R+) ;
6) a¶b¶0=⇒a2¾b2(décroissance de x7→ x2sur R−).
Définition 3.2 — Minorant, majorant
Soit Eune partie de R.
On dit que m∈Rest un minorant de Esi et seulement si ∀x∈E,m¶x.
On dit que M∈Rest un majorant de Esi et seulement si ∀x∈E,M¾x.
Définition 3.3 — Plus petit élément, plus grand élément
Soit Eune partie de R.
On dit que x0est le plus petit élément de Esi et seulement si
x0∈E,et ∀x∈E,x0¶x
On le note alors min(E).
On dit que x0est le plus grand élément de Esi et seulement si
x0∈E,et ∀x∈E,x0¾x
On le note alors max(E).
Définition 3.4 — Borne supérieure, borne inférieure
Si l’ensemble des majorants de E admet un plus petit élément, on dit que c’est la
borne supérieure de E. Notation : sup(E).
Si l’ensemble des minorants de E admet un plus grand élément, on dit que c’est la
borne inférieure de E. Notation : inf(E).

IV — Valeur absolue 3
IV — Valeur absolue
Définition 4.1 — Valeur absolue
La fonction valeur absolue est définie par
∀x∈R,|x|déf. =xx¾0et |x|déf. =−xx<0
Si x et y sont deux réels, |x−y| s’interprète comme la distance, sur la droite
réelle, entre xet y.
y x
|x−y|
Propriété 4.2 — Soit (x,y)∈R2et n∈N
–|x|¾0;
–|x|=0⇐⇒ x=0;
–|x|=|−x|
–|x|2=x2 et donc
px2=|x|
;
–|x y|=|x||y|et |xn|=|x|n;
–|1/y|=1/|y| et |x/y|=
|x|/|y|;
Théorème 4.3 — Inégalités et valeur absolue
Soit (x,y)∈R2
–|x|¶y⇐⇒ −y¶x¶y;
–∀x∈R,x¶|x|
–∀(x,y)∈R2,|x+y|¶|x|+|y|(inégalité triangulaire);
–∀(x,y)∈R2,|x−y|¶|x|+|y|;