QCM sur la trigonométrie Vestibular

QCM sur la trigonométrie Vestibular
Fuvest 2009
Exercice 1
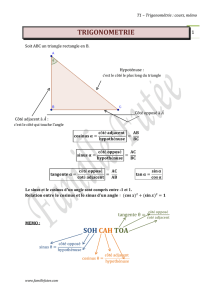
Sur la figure ci-dessous, B,Cet Dsont trois points distincts d’un cercle de centre O.
Aest un point extérieur à ce cercle.
De plus,
•A,Bet Csont alignés ;
•A,Oet Dsont alignés ;
•AB =OB ;
•
\
COD mesure αradians.
A O
D
C
B
Dans ces conditions, la mesure de l’angle
\
ABO, en radians, est :
1) π−
α
4
2) π−
α
2
3) π−2α
3
4) π−3α
4
5) π−3α
2
D. LE FUR 1/ 24

QCM sur la trigonométrie Vestibular
Exercice 2
Les longueurs des côtés d’un triangle ABC forment une progression arithmétique.
On sait de plus que le périmètre de ce triangle vaut 15 et que son angle b Amesure 120o.
Alors, le produit des longueurs de côtés est égal à :
1) 25
2) 45
3) 75
4) 105
5) 125
D. LE FUR 2/ 24

QCM sur la trigonométrie Vestibular
Exercice 3
Un angle θformé par deux plans αet βest tel que tan θ=√5
5.
Le point Pappartient au plan αet est à une distance 1du plan β.
Alors, la distance de Pà la droite d’intersection de αet βest égale à :
1) √3
2) √5
3) √6
4) √7
5) √8
D. LE FUR 3/ 24

QCM sur la trigonométrie Vestibular
Fuvest 2008
Exercice 1
Pour calculer la hauteur d’une tour, on utilise le procédé suivant : un appareil de hauteur négligeable est placé au
sol à une certaine distance de la tour, et émet un rayon en direction du sommet de la tour.
L’angle lu entre le sol et le rayon est de α=π
3radians.
Ensuite, on déplace l’appareil de 4mvers la tour. L’angle ainsi obtenu est de βradians, avec tan β= 3√3.
On peut affirmer que la hauteur de la tour est :
1) 4√3
2) 5√3
3) 6√3
4) 7√3
5) 8√3
αβ
D. LE FUR 4/ 24

QCM sur la trigonométrie Vestibular
Exercice 2
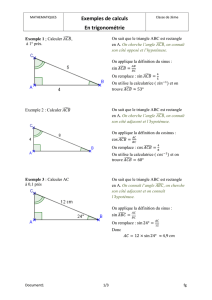
Le triangle ACD est isocèle de sommet principal A.
Le segment [OA]est perpendiculaire au plan contenant le triangle OCD, comme le montre la figure suivante :
O
C
D
A
Sachant que OA = 3,AC = 5 et sin
\
OCD =1
3, alors, l’aire du triangle OCD est :
1) 16√2
9
2) 32√2
9
3) 48√2
9
4) 64√2
9
5) 80√2
9
D. LE FUR 5/ 24