Formule trigo

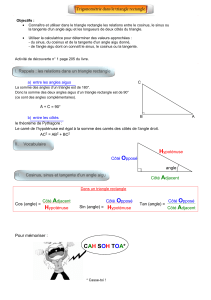
Formule trigonométrique : cosinus
En 4ème, on a découvert un nouvel outil appelé « cosinus ».
Cet outil s’utilise uniquement dans les triangles rectangles.
Le cosinus d’un angle aigu est égal au rapport :
Ce rapport ne dépend que de la mesure de l’angle considéré.
La valeur du cosinus d’un angle est toujours comprise entre 0 et 1.
Avant de commencer ….
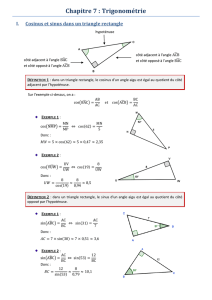
Dans chaque cas, l’hypoténuse du triangle rectangle est surlignée en couleur.

Dans chaque cas, le côté adjacent de l’angle indiqué est surligné en couleur.
J’utilise ma calculatrice ….
Avant d’utiliser la calculatrice, il faut vérifier qu’elle est bien en mode degrés.
Voici un exemple de tableau montrant quelques valeurs de cosinus.
Les mesures d’angles sont arrondies à 1° près et les valeurs de cosinus sont arrondies à 0,01 rès :

Activité : préliminaires
OAB est un triangle rectangle en A .
On place un point C sur le segment [OA], puis on trace la perpendiculaire à (OA) passant par C,
elle coupe [OB] en D.
1) Faire une figure à main levée.

2) Que peut-on dire des droites (AB) et (CD) ? Justifier.
On sait que :
• les droites (AB) et (CD) sont perpendiculaires à une même droite (OA)
Or :
si deux droites sont perpendiculaires à une même droite alors elles sont parallèles entre elles
Donc :
(AB) // (CD)
Activité : un nouveau rapport
3) Montrer que :

En déduire que :
On sait que :
• les points O, C, A sont alignés ainsi que les points O, D, B
• (AB) // (CD)
Or :
d’après la propriété de Thalès, on a :
On a donc :
On utilise enfin le « produit en croix » :
Puis on divise les deux membres par OD ×OB :
En simplifiant, on obtient donc :