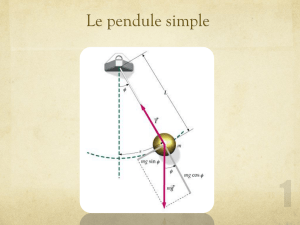
Aspect énergétique de la mécanique du point

Aspect énergétique de la mécanique du point
I Travail d’une force. Théorème de l’énergie cinétique
A) Puissance – travail élémentaire

On considère un référentiel (R) et un point matériel, soumis à une force F , qui se

déplace de M à M’ infiniment voisins. Travail de F sur ce déplacement :



W ( F )  F  MM '  F  d OM

d OM  v M /( R )  dt

 
Donc W ( F )  F  v M /( R )  dt

Puissance (instantanée) de F :

 W ( F )  
P( F ) 
 F  vM /( R )
dt
W   J ; P  W
B) Travail d’une force
B
d OM
M
A

M se déplace de A vers B, soumis à une force F dépendant éventuellement de la
position et du temps.




WAB ( F ) "  W(F) "    W(F)    F ( M )  d OM
AB
M allant de
Aà B
AB

Travail de F pour un déplacement de A à B

 

W ( F )  F  vM /( R )  dt  P( F )dt



tB
Donc WAB ( F )    P( F )dt   P( F )dt
AB
tA
C) Exemples
1) Forces perpendiculaires au déplacement

R

g

P


Travail élémentaire de R :

 
 
W ( R)  R  vM /( R )  dt  0 car R  vM /( R )


Donc WAB ( R)    W(R)  0
AB
O fixe dans (R)

l

T
M(m)

P

e

e






W (T )  T  d OM  T  l  d .e  0 car e  T
2) Force constante

On considère une force F indépendante de la position et du temps
(exemple : le poids à petite échelle)





B
WAB ( F )   F
  d OM  F   d
 OM  F  OM A  F  AB
AB
AB
 
3)


F  .v M /( R )


 
2

W ( F )  F  d OM  F  v M /( R ) dt   v M /( R ) dt  .v 2 dt
Supposons que M se déplace à module de vitesse constante :

v M /( R )  v0


L  A B  Longueur de A B

AB L
tB  t A 

v0
v0

W AB ( F )   - .v 02 dt  -.v 02 (t B  t A )  .v0 L

AB

Donc le travail de F dépend du chemin suivi et de la vitesse.

Remarque : F n’est constante que si M se déplace à vecteur vitesse



constant, et ainsi WAB ( F ) vérifie aussi WAB ( F )  F  AB
4) Energie cinétique
a) Définition
Dans un référentiel (R), on considère un point matériel M de masse m,
2

1
1 
de vitesse vM /(R ) . Alors EC  m.v M2 /( R )  m v M /( R )
2
2
b) Théorème de l’énergie cinétique
On considère un référentiel (R) galiléen, un point matériel M de masse

m soumis à une résultante des forces F .
On a :


dEC /( R ) 1  dv M /( R ) 
dv M /( R ) 



  m.a M /( R )  vM /( R )
 m
 v M /( R )  vM /( R ) .
dt
2  dt
dt 
(R) est galiléen.


Donc, d’après la relation fondamentale de la dynamique, F  m.a M /( R )

 
dEC /( R )
 P( F )
 F  v M /( R ) 
dt
dt

 

Ou dEC /( R )  F  v M /( R ) .dt  F  d OM soit dEC /( R )  W ( F )
Donc
dEC /( R )
Forme intégrale :


1
EC ( B)  EC ( A)  WAB ( F ) , ou m(v B2  v A2 )  W AB ( F )
2
5) Application du théorème de l’énergie cinétique
a) Saut à ski
A

g
B
Un skieur part de A avec une vitesse nulle. Avec quelle vitesse décolle
t’il en B ? (On néglige les frottements)
 

1
ECB  EC A  m.v B2  W AB ( R  P)  W AB ( P)
2
1
m.v B2  mgh (avec h  z A  z B )
2
Donc v B  2 gh
b) Tir balistique

g
z
zflèche
A

v0

x
x  v0 cos  indépendante du temps.
D’après le théorème de l’énergie cinétique appliqué à M entre O et A :

1
1
m.v A2  m.vO2  WO A ( P )   mg ( z A  z 0 )   mgzflèche
2
2

et v A  v0 cos  car v A // Ox
1
1
m.v02 cos 2   m.vO2   mgzflèche
2
2
2
2
v sin 
Soit z flèche  0
2g
Donc
II Energie potentielle
A) Force conservative


F est dite conservative lorsque, pour tous points A et B de l’espace, W AB ( F ) ne


dépend que de A et B et non pas de A B , soit W AB ( F )  f ( A, B)
Cas particulier :
A

Pour une boucle fermée, W A A ( F )  0
Exemple : le poids, une force constante.

Contre-exemple : frottement (pour une boucle, v  cte , et sinon dépend du chemin)
B) Energie potentielle

On considère une force F conservative, et O fixe dans (R).
B
A
O

F est conservative.





Donc WAB ( F )  WAO ( F )  WOB ( F )  WAO ( F )  WBO ( F )  f ( A, O)  f ( B, O)
On définit la fonction EP : M  EP (M )  f (M , O)

Ainsi, W AB ( F )  f ( A, O)  f ( B, O)  E P ( A)  E P ( B)

EP est l’énergie potentielle de M dans le champ de force F .

(On dit que F dérive de l’énergie potentielle EP )
Soit E P ' une autre fonction énergie potentielle. Soit A un point de l’espace.

Pour tout M de l’espace, on a : W AM ( F )  E P ( A)  E P ( M )  E P ' ( A)  E P ' ( M )
Donc E P ' ( M )  E P ( M )  ( E P ' ( A)  E P ( A))

cte indépendante de M
Donc EP '  EP  cte
Définition différentielle : Pour un déplacement infinitésimal de M à M’, on a :



WM M ' ( F )  F  MM '  F  d OM
 EP ( M )  EP ( M ' )  dEP ( M )

Donc l’énergie potentielle est la fonction telle que W ( F )  dE P ( M )
Méthode : On calcule W . Si on peut écrire W sous la forme W  dE P , alors

F est conservative et EP (cte) est une énergie potentielle.
C) Exemples
1) Energie potentielle de pesanteur Epp.






W ( P)  P  d OM  mgk  (dx  i  dy  j  dz  k )  mgdz  dmgz
Donc EPP  mgz  cte
2) Energie potentielle élastique
O
k,l0

x

e
M e

On note r  OM
M se déplace dans le plan.

T : tension du ressort



T  k (l  l 0 )  e   k (r  l 0 )  e 





1
W (T )  T  d OM  T  (dr  e   rd  e )  k (r  l 0 )dr  d ( k (r  l 0 ) 2 )
2
1
1
Donc E PE  k (r  l 0 ) 2  cte  kX 2  cte
2
2
III Energie mécanique
A) Définition
E pi

M est soumis dans (R) galiléen à Fi forces conservatives d’énergies potentielles

et F j forces non conservatives.
On pose Em  EC   E Pi
i
B) Théorème de l’énergie mécanique
D’après le théorème de l’énergie cinétique appliqué à M dans (R) galiléen, on a :


dEC   W ( Fi )   W ( F j )


 j
i
  dEPi

 dEC   dE Pi   W ( F j )
i
j

 d ( EC   E Pi )   W ( F j )
i

 dEm   W ( Fj )
j
j

dE m
  P( F j )
dt
j
En intégrant la première relation, on obtient :

Em  Em ( B)  Em ( A)  WAB ( F j )
Ou
j
Cas particulier : un système est dit conservatif lorsque E m  cte
C) Intégrale première du mouvement
L’intégrale première du mouvement, c’est l’équation différentielle du premier
ordre obtenue par application du théorème de l’énergie mécanique pour un système
conservatif.
1) Ressort horizontal
O
A
M
x
l0
x  OM  l  l 0

OM  x  i
Bilan des forces :



P  mg  mgk


R  R z k (pas de frottement s)



T  k (l  l 0 )  i  kx  i
On a :
1
1
E m  mx 2  mgz  kx 2
2
2

k

i
D’après le théorème de l’énergie mécanique,

dE m  W ( R)  0
1 2
1
mx  mgz  kx 2
2
2
L’altitude z ne change pas.
1
1
Donc E m  mx 2  kx2  cte (intégrale première du mouvement)
2
2
On a donc :
dEm
1
1
 0  m(2 xx)  k (2 xx)  0  mxx  kxx  0
dt
2
2
L’équation différentielle du mouvement est donc :
mx  kx  0 (cas x  0 sans intérêt)
Donc E m  cte 
2) Pendule simple
A fixe dans (RT) galiléen

l

g

T 
u
M(m)
 
P uR








AM  l  u R ; P  mg ; v M /( RT )  l  u ; T // AM , T  TR u R

1
1
m  v M2 /( RT )  E PP  m  l 2   2  mgz
2
2
On a z  AH  l cos
1
Donc E m  m  l 2   2  mg  l cos 
2
D’après le théorème de l’énergie mécanique :

 
dEm
 P(T )  0 (car T  v )
dt
Donc m  l 2      mg  l   sin   0
 l 2    g  l sin   0 (cas   0 sans intérêt)
Em 
IV Utilisation de l’énergie potentielle pour l’étude du mouvement
Dans cette partie, on ne considère que des systèmes conservatifs
A) Applications
- M a un mouvement rectiligne uniforme sur un axe (Ox , résultante des forces


F  F ( x)  i
On a :




W ( F )  F  d OM  ( F ( x)  i )  (dx  i )  F ( x)dx

et W ( F )  dE P
dE
Donc F ( x)   P
dx
- M décrit un mouvement circulaire de centre O, de rayon R, repéré par un angle  .
O
R


u
M

uR



F  FR ( )  u R  F ( )  u

OM  R  u R

d OM  Rd   u
On a :


W ( F )  F  d OM  F ( ) Rd

et W ( F )  dE P
1 dE P
Donc F ( )  
R d
B) Diagramme d’énergie potentielle
Graphe de E p (x) :
EP
 
F 0

F dirigée dans le même sens que le

F dirigée dans le sens
x
opposé au mouvement
mouvement
C) Position d’équilibre et stabilité
dE P
 0  la courbe de E p
dx
présente une tangente horizontale en cette position d’équilibre.
Stabilité d’une position d’équilibre x 0 :


F
F'
M est à l’équilibre dans (R) galiléen  F ( x)  0 
x2
x0
(équilibre stable)
x1
dE P
0
dx
dE P
Si x 2  x0 , F ( x)  0, c' est à dire
0
dx
Si x1  x0 , F ( x)  0, c' est à dire
dE P
dx
x0
d 2 EP
dEP
est croissante si, et seulement si
0
dx
dx 2
Donc :
d 2 EP
Lorsque
 0 , l’équilibre est stable.
dx 2
d 2 EP
Lorsque
 0 , l’équilibre est instable.
dx 2
d 2 EP
Lorsque
 0 , on ne peut pas conclure.
dx 2
Stable
Instable
Instable
Indifférent
D) Etude qualitative du mouvement
1 2
1
mv  E P ( x)  mv 2  E m  E P ( x)  0
2
2
Donc E m  E P ( x)
Em 
Ep
Em
x
x0
Donc x  x0 ; x0 correspond à une barrière de potentiel que x ne peut pas dépasser
Ep
Em
x1
x2
x
E P ( x)  Em  x  x1 ; x2  .
On a donc un mouvement borné : cuvette ou point de potentiel.
E) Etude de petits mouvements autour d’un équilibre stable
1) Développement de Taylor d’une fonction n fois dérivable
Soit F : x  F ( x) n fois dérivable, de dérivée n-ième continue en x 0 .
Développement limité de F en x 0 à l’ordre n, formule de Taylor :
F ( x0  h)  F ( x0 )  hF ' ( x0 ) 
h2
h n (n)
F ' ' ( x0 )  ... 
F ( x 0 )  h n  ( h)
2
n!
où  (h) h
 0
0
Cas particuliers :
n  0 : F ( x)  F ( x0 )   ( x  x0 )
n  1 : F ( x)  F ( x0 )  ( x  x0 ) F ' ( x0 )  ( x  x0 ) ( x  x0 )
n  2 : F ( x)  F ( x0 )  ( x  x0 ) F ' ( x0 ) 
( x  x0 ) 2
F ' ' ( x0 )  ( x  x0 ) 2  ( x  x0 )
2
Exemple :
ex  1 x 
x2 x3
xn

 ... 
 x n  ( x)
2
3!
n!
2) Développement limité de l’énergie potentielle au voisinage de x0, position
d’équilibre stable.
Formule de Taylor à l’ordre 2 au voisinage de x 0 :
E P ( x)  E P ( x0 )  ( x  x0 )
( x  x0 ) 2 d 2 E P
dE P
( x0 ) 
( x 0 )  o( x )
2
dx
2
dx




 0 car position
d'équilibre
0
Ainsi, au voisinage de x 0 :
( x  x0 ) 2 d 2 E P
1 2

E m  mx  E P ( x0 ) 
( x0 )
2
2
dx 2
On pose h  x  x0 on a alors h  x ; h  x
On a :
dE m
 0 (système conservati f)
dt
1 d 2 EP
 mxx 
( x0 )  2( x  x0 ) x  0
2 dx 2
d 2 EP
 mhh 
( x0 )  hh  0
dx 2


d 2 EP
 h mh 
( x0 )  h   0
2
dx


2
1 d EP
( x0 )  h  0 ; h   2  h  0
Donc h 
2
m 
dx 



0
 2
Donc h(t )  A cos .t  B sin .t on a donc un mouvement borné.
A et B sont déterminés par les conditions initiales :
h(0)  x(0)  x0
h(0)  x (0)
Les caractéristiques du mouvement sont donc déterminées par les propriétés
locales de l’énergie potentielle.
Remarque :
d 2 EP
 dE P

Si
( x0 )  0  et
( x0 )  0, c' est à dire que l' équilibre est instable 
2
dx
dx


2
1 d EP
On aura
( x0 )  0
2
m
dx




  2
Donc h vérifie h  2 h  0
Donc h(t )  Ae t  Be t . On a ainsi un mouvement non borné (du moins
tant que l’approximation du développement limité reste valable)
F) Application : le pendule simple
A

g

O
l
M(m)
E P  mgz  mgl(1  cos  )  mgl cos   mgl
EC 
1 2 1 2 2
mv  ml 
2
2
E P ( )
2mgl

2

Positions d’équilibre et stabilité :
dE P
 mgl sin 
d
dE P
à l’équilibre,
 0 , soit   0  
d
d 2 EP
 mgl cos 
d 2
d 2 EP
Pour   0 2 ,
 mgl  0 l' équilibre est donc stable
d 2
d 2 EP
Pour    2 ,
 mgl  0 l' équilibre est donc instable
d 2
Etude qualitative du mouvement :
Pour des conditions initiales données  (0)   0    ;   ; (0)  0 ,
1
E m (t )  mgl (1  cos  0 )  ml 202
2
1er cas : E m  2mgl  deux barrières de potentiel en 1 et  1 . Le pendule
oscille entre ces deux valeurs (mouvement oscillatoire borné)
A
 1 1
M(m)
2ème cas : Em  2mgl  pas de barrière de potentiel.
1 2
mv  E m  E P ( )

2
2 mgl

 2 mgl  2 mgl
Donc v  0, t . Donc  garde un signe constant à tout instant.
On a alors un mouvement de type fronde :

t
Ici,   0,  0  0
Petits mouvements autour des positions d’équilibre stable
Le seul équilibre stable est pour  0  0 (il y a une position d’équilibre en  0  
mais instable)
Développement de EP ( ) au voisinage de  0 :
dE P
d 2 EP
E P ( )  mgl(1  cos  ) ;
 mgl sin  ;
 mgl cos 
d
d 2
dE P
 2 d 2 EP
Donc E P ( )  E P (0)  
(0) 
(0)  o( 2 )
d
2 d 2
dE P
d 2 EP
E P (0)  mgl(1  cos 0)  0 ;
(0)  mgl sin 0  0 ;
(0)  mgl
d
d 2
Donc E P ( ) 
2
2
mgl (pour  proche de 0)
1 2 2
2
E m  ml   mgl
2
2
dE m
g
 0  ml 2  mgl  0      0 (  0)
dt
l
g
On a donc une solution sinusoïdale de pulsation  
l
V Portrait de phase
A) Définition
On suppose M en mouvement rectiligne, d’équation horaire x(t ) (conditions
initiales données). La trajectoire de phase est la courbe d’équation paramétrique :
 X  x(t )

 Y  x (t )
Plan de phase :
Le portrait de phase est l’ensemble des trajectoires de phases pour des conditions
initiales différentes.
B) Propriétés
x
Trajectoire de gauche à droite
x (t )
x
x(t)
Minimum local de x
Tangente horizontale
Maximum local de x
Trajectoire de droite à gauche
A un instant t, si x (t )  0 , x est croissante au voisinage de t
Pour t '  t (si x reste positive), x(t ' )  x (t ) . Ainsi, dans le plan d’ordonnées
positives, les trajectoires vont de gauche à droite. Inversement, dans le plan d’ordonnées
négatives, les trajectoires vont de droite à gauche.
Si x  0 , x admet un extremum (c'est-à-dire une tangente verticale pour la
trajectoire de phase), ou une tangente horizontale.
Il n’y a pas en général d’intersections, au même instant t, entre les trajectoires de
phase associées à des conditions initiales différentes : s’il y a une intersection en
M ( x1 , x1 ) , alors l’équation différentielle x  f (x) aurait deux solutions si on prend
( x1 , x1 ) comme conditions initiales, ce qui et impossible. (Mais on peut avoir une
intersection si les deux trajectoires ne se coupent pas au même instant).
Si la trajectoire est fermée, cela signifie que le point matériel a un mouvement
périodique.
Pour un mouvement avec frottements, (le système est alors non conservatif),
l’énergie mécanique diminue.
La trajectoire de phase donne :
C) Application au portrait de phase d’un pendule simple
Petites oscillations autour de  0  0 :
   2  0 , avec  
g
l
Donc   A cos(.t   ) ;    A sin( .t   ) (A : amplitude des oscillations)
On a alors :
  A cos(.t   )
 /   A sin( .t   )
2
  
Donc     2  A 2 ; la trajectoire est un cercle de rayon A :
 
 / 
M(t)
O
A
θ
En faisant varier A, on obtient un autre cercle de centre O.
En faisant varier  , on obtient le même cercle décalé dans le temps.
Si Em  2mgl : on a un mouvement de type fronde,  garde un signe constant :
 / 
Sens trigonométrique
0

2

Sens horaire
(Les courbes ne sont pas forcément exactement sinusoïdales)
Cas particulier Em  2mgl . E c s’annule donc pour    2  (ensuite, soit le
pendule continue, soit il fait demi-tour)
Cas E m  2mgl : on a un mouvement circulaire borné :
 / 
0

Les trois graphiques regroupés forment le portrait de phase :