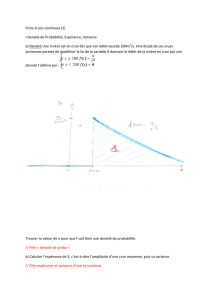
Probabilités, MATH 424 Feuille de travaux dirigés 5 : Variables

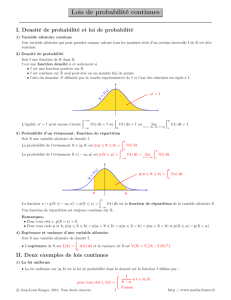
Probabilités, MATH 424
Feuille de travaux dirigés 5 : Variables aléatoires à densité (Solutions)
Solution 1. On considère une variable aléatoire X de densité
2
cx 0 ≤ x ≤ 3
f (x) =
0
sinon
1. La fonction f est continue par morceaux, positive et intégrable sur R. Cette fonction est une densité de probabilité si
Z
f (x)dx = 1.
R
Or
Z
R
1
f (x)dx = cx3
3
3
= 9c.
0
On conclut donc que f est une densité si et seulement si c = 19 .
Rx
2. La fonction de répartition F de X est par définition la fonction x 7→
Par conséquent :
– Si x ≤ 0, F(x) = 0.
1 3
– Si x ∈ [0, 3] alors F(x) = 27
x
– Si x ≥ 3 alors F(x) = 1.
−∞
f (t)dt.
3. La probabilité P(1 < X < 2) est donnée par la formule
P(1 < X < 2) = F(2) − F(1) =
4. Nous avons
Z
E(X) =
x f (x)dx =
R
Nous avons
E(X 2 ) =
Z
x2 f (x)dx =
R
1
9
Z 3
1
9
Z 3
0
7
.
27
9
x3 dx = .
4
x4 dx =
0
27
.
5
Solution 2 (Loi uniforme). Soit X une variable aléatoire qui suit une loi uniforme sur le segment [0, 1].
1. La fonction de répartition de X est la fonction
x 7→
Z x
Z
f (t)dt =
−∞
donc
1dt
]−∞,x]∩[0,1]

x≤0
 0 si
x si x ∈ [0, 1] .
F(x) =

1 si
x≥1
2. La moyenne de X est donnée par
Z 1
Z
E(X) =
x f (x)dx =
0
R
1
xdx = .
2
La variance de X est donnée par la formule
2
2
Var(X) = E(X ) − E(X) =
Z 1
0
1
x2 dx −
1
1
= .
4 12
3. Soit n ∈ N. Par application du théorème de transfert l’espérance de la variable aléatoire X n est
E(X n ) =
Z 1
xn dx =
0
1
.
n+1
4. Soit a et b deux réels avec a < b. La loi uniforme sur [a, b] a pour densité de probabilité la fonction
f (x) = 0 si x ∈
/ [a, b]
1
f (x) = b−a
si x ∈ [a, b]
2
(b−a)
On a E(X) = a+b
2 et Var(X) = 12 .
Détaillons le calcul de la variance :
1
Var(X) =
b−a
Z b
a
1
x dx −
b−a
2
donc
1 1 3
1
Var(X) =
(b − a3 ) −
b−a 3
(b − a)2
donc
2
Z b
xdx
a
2
1 2
2
(b − a )
2
1
1
1
Var(X) = (b2 + ab + a2 ) − (a2 + 2ab + b2 ) = (b − a)2 .
3
4
12
Solution 3 (Loi exponentielle). Soit λ > 0 fixé. On dit que X suit une loi exponentielle de paramètre λ si X admet pour
densité la fonction
f (x) = λe−λx 1x≥0 .
On note alors X ∼ E (λ).
1. La fonction f est continue et positive sur R. Elle est nulle sur R− . Pour tout A > 0 nous avons
Z A
0
Par conséquent
R
R
f (x)dx = [−e−λx ]A0 = 1 − e−λA → 1.
A→+∞
f (x)dx = 1. Nous concluons donc que f est une densité sur R.
2. La fonction de répartition F est définie par
Z x
F(x) =
f (t)dt
−∞
Par conséquent
– si x ≤ 0 alors F(x) = 0 car f est nulle sur l’intervalle ] − ∞, x].
– si x ≥ 0 alors
Z
x
F(x) =
0
f (t)dt = [−e−λt ]x0 = 1 − e−λx .
3. Par définition, l’espérance de X est
Z
E(X) =
x f (x)dx
R
sous réserve que la fonction x 7→ x f (x) soit intégrable sur R.
Cette fonction est continue sur R, positive sur R et nulle sur ] − ∞, 0]. Soit A > 0, on calcule par intégration par parties
l’intégrale
Z A
Z A
1
1
1 − e−λA →
.
λxe−λx dx = [−xe−λx ]A0 +
e−λx dx = −Ae−λA +
A→+∞ λ
λ
0
0
Par définition la variance de X est
Z +∞
2
Z +∞
2
2
2 −λx
−λx
Var(X) = E(X ) − E(X) =
λx e dx −
xe dx ,
0
2
0
sous réserve que toutes ces intégrales de fonctions continues positives soient finies.
Classiquement, on montre l’intégrabilité au voisinage de l’infini de ces fonctions par comparaison avec la fonction
qui est intégrable au voisinage de +∞. On utilise pour cela le théorème de croissance comparée :
1
x2
lim x2 (x2 e−λx ) = 0 et lim x2 (xe−λx ) = 0
x→∞
x→∞
car λ > 0 donc x2 e−λx = o x2 et xe−λx = o x2 ce qui montre par les théorèmes de comparaison que ces intégrales
sont finies et donc que X admet une variance.
Néanmoins, comme nous Rdevons calculer la variance on peut procéder comme suit : soit A > 0, par double intégration
par partie nous calculons 0A x2 λe−λx dx :
A A
Z A
h
iA 2
2
2
x2 λe−λx dx = −x2 e−λx + − xe−λx + − 2 xe−λx → 2
0
λ
λ
λ
0
0
0
1
1
nous obtenons alors
Z A
Z
A
2
1
.
A→+∞ 0
λ2
0
Ceci remontre à postériori que ces intégrales sont finies et que la variable aléatoire admet effectivement une variance
qui vaut
1
Var(X) = 2 .
λ
4. Montrons que la loi exponentielle a la propriété d’abscence de mémoire :
lim
2
−λx
x λe
dx −
2
−λx
x λe
dx
=
∀(x,t) ∈ R+ × R+ , P(X > x + t | X > x) = P(X > t).
Soit (x,t) ∈ R+ × R+ . Nous avons
P(X > x + t | X > x) =
P(X > x + t et X > x) P(X > x + t) e−λ(x+t)
=
= −λx = e−λt = P(X > t).
P(X > x)
P(X > x)
e
On rappelle que pour tout x ≥ 0
P(X > x) = 1 − P(X ≤ x) = 1 − (1 − e−λx ) = e−λx .
5. La durée de vie en nombre d’années d’une télévision suit une loi de densité
1 t
f (t) = e− 8 1t≥0 .
8
(a) La durée de vie moyenne d’une télévision est donc l’espérance de cette variable aléatoire soit 8 années. L’écart
type de cette variable est 8 ans.
(b) La probabilité pour qu’une télévision ait une durée de vie supérieure à 8 ans est
P(X ≥ 8) = e−1 .
(c) Nous possédons une télévision depuis 2 ans, la probabilité que sa durée de vie soit encore d’au moins 8 ans est
donnée par
P(X ≥ 10 | X ≥ 2) = P(X ≥ 8) = e−1 .
Solution 4. (Loi normale). Un poète écrit des poèmes dont le nombre de vers suit une loi normale de moyenne 20 et d’écart
type 5. On ouvre son recueil au hasard et on choisit un poème. La densité de cette loi est donc la fonction
!
1 x − 20 2
1
.
f (x) = √ exp −
2
5
5 2π
Le graphe de cette fonction est symétrique par rapport à la droite d’équation x = 20. L’intégrale de cette fonction vaut 1. Par
conséquent
Z 20
Z +∞
1
f (x)dx =
f (x)dx = .
2
−∞
20
3
1. La probabilité pour que le poème fasse plus de 20 vers est
P(X ≥ 20) =
Z +∞
20
1
f (t)dt = .
2
2. La probabilité pour que le poème fasse moins de 20 vers est
P(X ≤ 20) =
Z 20
−∞
1
f (t)dt = .
2
3. La probabilité pour que le poème fasse plus de 25, 30, 35, 40 vers est
P(X ≥ 25) = 0.16, P(X ≥ 30) = 0.02, P(X ≥ 35) = 0.001, P(X ≥ 40) = 0.0003.
4. La probabilité pour que le poème fasse moins de 10 vers se calcule par symétrie du graphe de la densité par rapport à
la droite x = 20
P(X ≤ 10) = P(X ≥ 30) = 0.02.
5. On peut améliorer la modélisation en jouant sur l’écart type. Par exemple si on prend un écart type de 15 vers au lieu
de 5 vers nous obtenons les probabilités plus réalistes
P(X ≥ 25) ' 0.30, P(X ≥ 30) = P(X ≤ 10) ' 0.15, P(X ≥ 40) ' 0.01.
Ceci montre bien que plus l’écart type est grand, moins la masse est concentrée autour de la moyenne.
Soit X une variable aléatoire suivant une loi normale.
1. On suppose que la moyenne est 12 et la variance est 4. La valeur q telle que P(X > q) = 0.1 correspond à la valeur q
telle que
X −µ q−µ
≤
= 0.9.
P(X ≤ q) = 0.9 = P
σ
σ
On utilise la table de la loi normale centrée et réduite pour obtenir
q−µ
= 1.28.
σ
Ce qui donne avec les µ = 12 et σ = 2 : q = 14.56.
2. On suppose que la moyenne est 5. Déterminons la variance pour que P(X > 9) = 0.2. On raisonne de même :
X −5 4
P(X > 9) = 0.2 ⇔ P(X ≤ 9) = 0.8 ⇔ P
≤
= 0.8
σ
σ
On utilise la table de la normale normale centrée et réduite pour obtenir
4
4
σ
' 0.84 c’est à dire σ ' 4.76.
Solution 5 (Densité). Pour savoir si Y admet une densité on considère sa fonction de répartition
FY = P(Y ≤ y).
Notons tout d’abord que toutes les valeurs de Y sont positives. Par conséquent pour tout y < 0, FY (y) = 0.
Notons de plus que
FY (0) = P(X 2 = 0) = P(X = 0) = 0.
√
Soit y > 0 et notons x = y. Nous avons
2
2
FY (y) = P(X ≤ x ) = P(−x ≤ X ≤ x) =
Z
Z
1dt =
[−x,x]∩[0,1]
1dt.
[0,x]∩[0,1]
Par conséquent

y≤0
 0 si
√
y si 0 ≤ y ≤ 1 .
FY (y) =

1 si
y≥1
Ceci montre que si Y a une densité, cette densité est la fonction

y≤0
 0 si
1
√
si
0
<
y≤1
f : y 7→
 2 y
0 si
y≥1
Solution 6 (Simulation d’une loi). Soit X une variable aléatoire de fonction de répartition F à valeurs dans ]0, 1[ et bijective.
1. La fonction de répartition F est croissante car pour x ≤ y nous avons par additivité de la mesure de probabilité P
F(y) = P(X ≤ y) = P(X ≤ x) + P(x < X ≤ y) ≥ P(X ≤ x) ≥ F(x).
De plus par hypothèse la fonction F est bijective, elle est donc injective et donc strictement croissante.
2. Soit x et y deux éléments de ]0, 1[ avec x < y. Nous avons F(F −1 (x)) = x et F(F −1 (y)) = y. La fonction F étant
strictement croissante, on déduit de l’inégalité x < y l’inégalité F −1 (x) < F −1 (y). Ce qui montre bien que la fonction
inverse F −1 est strictement croissante.
3. Grâce à la touche “rand” de la calculatrice, on tire une variable uniforme U sur ]0, 1[. On considère la variable aléatoire
Y = F −1 (U). Pour déterminer la loi de Y on considère sa fonction de répartition. Soit y ∈ R.
FY (y) = P(Y ≤ y) = P(F −1 (U) ≤ y) = P(U ≤ F(y)).
La dernière égalité étant obtenue croissance de F. Ainsi, nous avons
FY (y) = FU (F(y)) = F(y).
Par conséquent X et Y ont la même fonction de répartition, elles suivent la même loi.
4. Pour simuler une loi X ayant une fonction de répartition F facilement inversible, on commence par simuler une loi
uniforme U sur ]0, 1[. La simulation induite par F −1 (U) sera une simulation de X.
5. Considérons une loi de Cauchy de densité f (x) =
répartition de X :
Z x
F(x) =
1
dt = lim
A→−∞
π(1
+ t 2)
−∞
Z x
A
1
.
π(1+x2 )
Pour la simuler il faut et il suffit d’inverser la fonction de
x
1
1
1 1
dt
=
lim
arctant
= + arctan(x).
A→−∞ π
π(1 + t 2 )
2 π
A
L’inverse de F est la fonction
π
F −1 : y 7→ tan πy −
.
2
Par conséquent pour simuler une loi de Cauchy, il suffit de simuler une loi uniforme sur ]0, 1[ puis d’appliquer la
fonction F −1 .
5
Solution 7. (Autour de l’indépendance).
Soit X = (X1 , X2 ) un couple de variables aléatoires définie sur un espace probabilisé (Ω, A , P).
1. On suppose que le couple suit une loi uniforme sur le carré [0, 1] × [0, 1]. Montrons que les variables aléatoires X1 et
X2 sont indépendantes et suivent chacune la loi uniforme sur [0, 1].
La loi marginale de la variable aléatoire X1 est donnée par la relation : pour tout intervalle I1 de R
P(X1 ∈ I1 ) = P((X1 , X2 ) ∈ I1 × R).
Par définition de la densité de la loi uniforme sur [0, 1] × [0, 1] nous obtenons l’égalité
P(X1 ∈ I1 ) =
Z
(x1 ,x2 )∈I1 ×R∩[0,1]×[0,1]
1dx1 dx2 .
Par le théorème de Fubini nous obtenons
P(X1 ∈ I1 ) =
Z 1
Z
x1 ∈I1 ∩[0,1] 0
Z
Z
dx1 dx2 =
x1 ∈I1 ∩[0,1]
dx1
0
1
dx2
Z
=
I1 ∩[0,1]
1dx1 .
Ce qui montre que la variable aléatoire X1 suit la loi uniforme sur [0, 1].
De même la variable aléatoire X2 suit la loi uniforme sur [0, 1].
Prouvons l’indépendance des deux variables X1 et X2 . Soit I1 et I2 deux intervalles de R, montrons que
P(X1 ∈ I1 et X2 ∈ I2 ) = P(X1 ∈ I1 )P(X2 ∈ I2 ).
Par définition nous avons
P(X1 ∈ I1 et X2 ∈ I2 ) =
Z
I1 ×I2 ∩[0,1]×[0,1]
1dx1 dx 2
Par le théorème de Fubini nous avons
P(X1 ∈ I1 et X2 ∈ I2 ) =
Z
Z
I1 ∩[0,1]
dx1
I2
dx2 = P(X1 ∈ I1 )P(X2 ∈ I2 ).
Remarquons aussi que :
• la densité de X1 est la fonction
f1 : x1 7→
Z
1[0,1]×[0,1] (x1 , x2 )dx2 = 1[0,1] (x1 ),
R
• la densité de X2 est la fonction
f2 : x2 7→
Z
1[0,1]×[0,1] (x1 , x2 )dx1 = 1[0,1] (x2 ),
R
• la densité du couple (X1 , X2 ) est égal au produit des densités (ce qui n’est pas toujours le cas !) :
1[0,1]×[0,1] = f1 f2 .
Ceci montre directement (par les théorèmes du cours) que les loi marginales sont des lois uniformes et qu’elles sont
indépendantes.
2. On suppose que le couple suit une loi uniforme sur le disque D(0, 1). La densité du couple est la fonction
f : x 7→
1
1
.
Aire(D(0, 1) D(0,1)
L’aire du disque est π.
Les lois marginales X1 et X2 admettent des densités données par
1
1D(0,1) (x1 , x2 )dx2 ,
Rπ
Z
f1 (x1 ) =
6
1
1D(0,1) (x1 , x2 )dx1 .
π
R
Z
f2 (x2 ) =
C’est à dire
f1 (x1 ) =
 √
q
R 1−x12 1

2

√
dx
=
1 − x12 si −1 < x1 < 1

2
2 π
π
−
1−x1



f2 (x2 ) =
0
sinon
 √
q
R 1−x2


 √ 2 2 π1 dx1 = π2 1 − x22 si −1 < x2 < 1
−



1−x2
0
sinon
Nous observons que le produit des densités f1 et f2 est différent de la densité du couple (X1 , X2 ) ce qui montre (par
le théorème du cours) que les variables aléatoires X1 et X2 ne sont pas indépendantes. On peut aussi considérer un
produit d’intervalles I × J de mesure non nulle et contenu dans le complémentaire du disque dans le carré unité. Nous
avons alors
P(X ∈ I × J) = 0
par définition de X. Alors que
P(X1 ∈ I)P(X2 ∈ J) 6= 0
ce qui montre que les variables aléatoires X1 et X2 ne sont pas indépendantes.
Par parité des densités f1 , f2 , f1 f2 nous observons que l’espérance des variables aléatoires X1 , X2 , X1 X2 est nulle. Cela
montre que la covariance du couple (X1 , X2 ) alors que les variables X1 et X2 ne sont pas indépendantes.
7