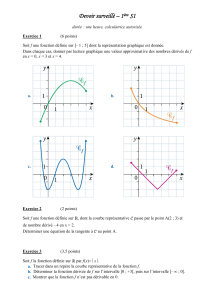
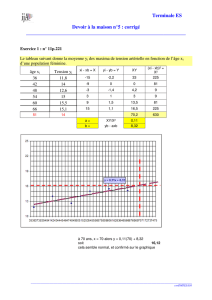
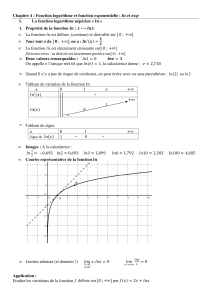
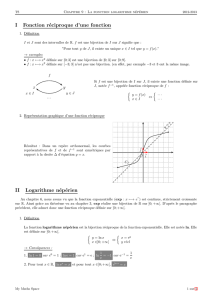
Fonctions usuelles

Fonctions usuelles
Rappels de BCPST 1
Généralités sur les fonctions
Dans ce qui suit, f désigne une fonction définie sur une partie D de l’ensemble R des
→
− →
−
réels et à valeurs dans R. Dans le plan muni d’un repère orthogonal (O, i , j ) l’ensemble des
points de coordonnées (x, f (x)) pour x variant dans D est appelé la courbe représentative de
f et sera noté Cf .
Parité, périodicité
Définition 1
On suppose que l’ensemble de définition D de f est tel que ∀x ∈ D, −x ∈ D.
• La fonction f est dite paire si ∀x ∈ D, f (−x) = f (x).
• La fonction f est dite impaire si ∀x ∈ D, f (−x) = −f (x).
Remarque La courbe représentative d’une fonction paire est symétrique par rapport à l’axe
des ordonnées ; celle d’une fonction impaire est symétrique par rapport à l’origine du repère.
Dans le cadre de l’étude d’une fonction, cette remarque permet de réduire le domaine d’étude
de la fonction.
Concrètement, pour obtenir la courbe représentative d’une fonction paire (resp. impaire), on
trace f sur D ∩ R+ et on complète par symétrie par rapport à l’axe des ordonnées (resp. par
rapport à l’origine).
Définition 2
Soit T ∈ R∗+ . On suppose que l’ensemble de définition D de f est tel que
∀x ∈ D, x + T ∈ D.
La fonction f est dite périodique de période T si ∀x ∈ D, f (x + T) = f (x).
Remarque Si une fonction est périodique de période T, elle est aussi périodique de période
2T, 3T, ... Généralement, on travaille avec la plus petite période possible. La périodicité d’une
fonction permet également de restreindre son domaine d’étude.
Concrètement, pour obtenir la courbe représentative d’une fonction périodique de période T,
on trace f sur D ∩ I où I est un intervalle de longueur T et on complète par les translations
→
−
de vecteur kT i pour k ∈ Z.
Fonctions majorées, minorées, borneés
Définition 3
• La fonction f est dite majorée si : ∃M ∈ R, ∀x ∈ D, f (x) 6 M.
• La fonction f est dite minorée si : ∃m ∈ R, ∀x ∈ D, f (x) > m.
• La fonction f est dite bornée si elle minorée et majorée ; ou, de façon équivalente,
si : ∃C ∈ R, ∀x ∈ D, |f (x)| 6 C.
1
Monotonie
L’étude de la monotonie d’une fonction permet de comprendre comment celle-ci varie.
Définition 4
• La fonction f est croissante (resp. strictement croissante) si :
∀(x, y) ∈ D 2 , x 6 y =⇒ f (x) 6 f (y) (resp. ∀(x, y) ∈ D 2 , x < y =⇒ f (x) < f (y)).
• La fonction f est décroissante (resp. strictement décroissante) si :
∀(x, y) ∈ D 2 , x 6 y =⇒ f (x) > f (y) (resp. ∀(x, y) ∈ D 2 , x < y =⇒ f (x) > f (y)).
• La fonction f est constante si : ∃k ∈ R, ∀x ∈ D, f (x) = k.
• Une fonction est alors dite monotone (resp. strictement monotone) sur D si elle
croissante sur D ou décroissante sur D (resp. strictement croissante sur D ou
strictement décroissante sur D).
Remarque Pour étudier la monotonie d’une fonction, on peut essayer de vérifier les définitions « à la main » ou bien, dans le cas d’une fonction dérivable, tenter de dériver la fonction
et d’étudier le signe de sa dérivée.
Opérations algébriques
Soient f et g deux fonctions définies sur une même partie D et à valeurs dans R. Soit λ
un réel. Il est possible de définir les opérations algébriques suivantes :
• la somme : h = f + g est la fonction définie sur D par
∀x ∈ D,
h(x) = f (x) + g(x)
• le produit par un scalaire : h = λf est la fonction définie sur D par
∀x ∈ D,
h(x) = λf (x)
• le produit : h = f g est la fonction définie sur D par
∀x ∈ D,
h(x) = f (x)g(x)
• le quotient : si g(x) 6= 0 pour tout x ∈ D, h =
∀x ∈ D,
f
est la fonction définie sur D par
g
h(x) =
f (x)
g(x)
Fonctions usuelles
Fonctions puissances d’exposant entier
On étudie ici les fonctions x 7→ xn pour n ∈ Z. Dans le cas n = 0, la fonction est constante
égale à 1 et l’étude est triviale. Nous allons discerner les cas où n > 0 et n < 0 (pour n < 0,
la fonction puissance a un problème de définition en 0).
2
Proposition 5
Soit n ∈ N∗ .
• La fonction f : x 7→ xn est définie et dérivable sur R de dérivée f 0 : x 7→ nxn−1 .
• Si n est pair, la fonction f est paire, strictement décroissante sur R− et strictement
croissante sur R+ .
• Si n est impair, la fonction f est impaire et constitue une bijection strictement
croissante de R sur lui-même.
Les représentations graphiques associées pour les cas n = 2, n = 4 et n = 3, n = 5 sont les
suivantes. Dans le cas pair, la courbe représentative est une parabole.
x2
x4
−2
4
4
3
3
2
2
1
1
−1
1
−2
2
−1
−1
−1
−2
−2
−3
−3
−4
−4
On rappelle que pour n > 0 et x ∈ R∗ , on pose x−n =
x5
x3
1
2
1
.
xn
Proposition 6
Soit n ∈ N∗ .
1
• La fonction f : x 7→ x−n = n est définie et dérivable sur R∗ de dérivée
x
−n
f 0 : x 7→ −nx−n−1 = n+1 .
x
• Si n est pair, la fonction f est paire, strictement croissante sur R− et strictement
décroissante sur R+ .
• Si n est impair, la fonction f est impaire, strictement décroissante sur R− et
strictement décroissante sur R+ .
Les représentations graphiques associées pour les cas n = 1 et n = 2 sont les suivantes. Dans
le cas impair, la courbe représentative est une hyperbole.
3
3
3
2
2
1
−2
1
x−1
−1
1
x−2
−2
2
−1
1
−1
−1
−2
−2
−3
−3
2
Fonction racine carrée
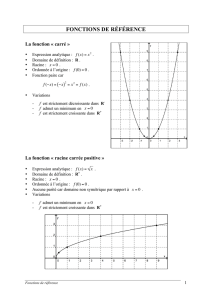
Proposition 7
La restriction de la fonction carré x 7→ x2 à R+ est une bijection strictement croissante de R+ sur R+ . Sa fonction réciproque est appelée fonction racine carrée et est
√
notée x 7→ x.
La fonction racine carrée est une bijection strictement croissante de R+ sur R+ ,
1
dérivable sur R∗+ de dérivée x 7→ √ .
2 x
Proposition 8
Soient x et y deux réels positifs.
√
√
• ( x)2 = x et
x2 = x
•
√
√ √
xy = x y
• Si y 6= 0,
r
√
x
x
= √
y
y
Remarque – Attention ! – Si x est un réel (pas nécessairement positif, cette fois),
√
x2 = |x|.
Les fonctions carré et racine carrée étant réciproques l’une de l’autre, leurs courbes représentatives sont symétriques par rapport à la droite d’équation y = x.
x2
y=x
3
√
2
1
0
1
2
3
4
4
5
x
Exponentielle et logarithme népérien
Définition 9
La fonction logarithme népérien, notée ln, est l’unique primitive sur R∗+ de la fonction
1
inverse x 7→ s’annulant en 1.
x
Z x
dt
∗
Autrement dit :
∀x ∈ R+ , ln(x) =
1 t
Proposition 10
1
.
x∗
• Le logarithme népérien est une bijection strictement croissante de R+ sur R.
• La fonction ln est définie et dérivable sur R∗+ de dérivée ln0 : x 7→
Proposition 11
Soient x et y deux réels strictement positifs.
1
x
• ln(xy) = ln(x) + ln(y)
• ln
x
y
= − ln(x)
• ln
= ln(x) − ln(y)
Remarque
On déduit immédiatement de cette proposition que si x ∈ R∗+ et n ∈ Z, on a
n
ln(x ) = n ln(x).
Définition 12
Le logarithme népérien réalisant une bijection de R∗+ sur R, on appelle fonction
exponentielle, notée exp, sa fonction réciproque.
Remarque Pour simplifier la notation, on introduit le nombre réel e = exp(1) et on notera,
pour tout réel x, exp(x) = ex .
Proposition 13
Soient x ∈ R et y ∈ R∗+ .
• ln(ex ) = x
• eln(y) = y
Proposition 14
• La fonction exponentielle est définie et dérivable sur R de dérivée exp0 : x 7→ exp x.
• La fonction exponentielle est une bijection strictement croissante de R sur R∗+ .
Remarque
Une exponentielle est toujours strictement positive : pour tout réel x, ex > 0.
Proposition 15
Soient x et y deux réels.
• ex+y = ex ey
• e−x =
5
1
ex
• ex−y =
ex
ey
Les fonctions logarithme népérien et exponentielle étant réciproques l’une de l’autre, leurs
courbes représentatives sont symétriques par rapport à la droite d’équation y = x.
y=x
ex
5
4
3
2
ln(x)
1
−1
1
2
3
4
5
−1
Pour le moment, nous connaissons les fonctions puissance x 7→ xn où n est un entier : si n > 0,
xn = x × . . . × x n fois et (si x 6= 0) x−n = 1/xn .
Il est naturel de vouloir étendre cette définition au cas où n est un réel. Cela est possible
si x > 0 à l’aide des fonctions exponentielle et logarithme népérien. En effet, les résultats
précédents suggèrent de poser, si x > 0 et b ∈ R,
xb = eb ln(x)
Remarque
Cette définition est cohérente avec la mise à la puissance n où n est entier. De
√
plus, si x ∈ R+ , x = x1/2
Fonctions exponentielles
Définition 16
Soit a ∈ R∗+ . La fonction exponentielle de base a est la fonction x 7→ ax = ex ln(a)
définie sur R.
Proposition 17
Soit a ∈ R∗+ \ {1} et f : x 7→ ax .
• La fonction f est définie et dérivable sur R de dérivée f 0 : x 7→ ln(a)ax .
• La fonction f est une bijection de R sur R∗+ strictement croissante si a > 1 et
strictement décroissante si 0 < a < 1.
Remarque
Si a = e ' 2, 71828, on retrouve que la fonction exponentielle f : x 7→ ex est
une bijection strictement croissante de R sur R∗+ de dérivée f 0 : x 7→ ex (puisque ln(e) = 1).
Les représentations graphiques associées dans les cas a = 1/2, a = 1 et a = 2 sont les
suivantes :
6
0, 5x
2x
5
4
3
2
1x
1
−5
−4
−3
−2
−1
1
2
3
4
5
Fonction logarithme décimal
Définition 18
La fonction logarithme décimal, notée log, est définie sur R∗+ par la formule
log(x) =
ln(x)
ln(10)
Proposition 19
• La fonction logarithme décimal est définie et dérivable sur R∗+ de dérivée
1
.
log0 : x 7→
x ln(10)
• La fonction logarithme décimal est une bijection strictement croissante de R∗+ sur
R.
Remarque
La fonction logarithme décimal ne différant de la fonction logarithme népérien
que d’un facteur 1/ ln(10), elle hérite des mêmes propriétés vis-à-vis du produit et du quotient
que le logarithme népérien (Proposition 11).
Proposition 20
La fonction logarithme décimal est la fonction réciproque de la fonction exponentielle
x 7→ 10x de base 10 : soient x ∈ R et y ∈ R∗+ ,
• log(10x ) = x
• 10log(y) = y
Fonctions puissances
Définition 21
Pour α ∈ R\Z, la fonction puissance d’exposant α est la fonction x 7→ xα = eα ln(x)
définie sur R∗+ .
7
Proposition 22
Soit α ∈ R\Z et f : x 7→ xα .
• La fonction f est définie et dérivable sur R∗+ de dérivée f 0 : x 7→ αxα−1 .
• La fonction f est une bijection de R∗+ sur R∗+ strictement croissante si α > 0 et
strictement décroissante si α < 0.
Les propriétés de calcul des fonctions puissances d’exposant entier s’étendent aux exposants
réels.
Proposition 23
Soient x et y deux réels strictement positifs et α et β deux réels.
• ln(xα ) = α ln(x)
• xα xβ = xα+β
xα
• β = xα−β
x
• (xy)α = xα y α
α β
αβ
• (x
)α= x α
x
x
= α
•
y
y
Les représentations graphiques associées dans les cas a = −0, 5, a = 1, 8, a = 1, a = 0, 6 et
a = 0 sont les suivantes :
x−0,5
x1,8
x
5
4
x0,6
3
2
x0
1
1
2
3
4
5
6
7
8
Fonction valeur absolue
Définition 24
La fonction valeur absolue, notée | · |, est la fonction définie pour tout x réel par
(
|x| =
x si x > 0
−x si x < 0
Proposition 25
• La fonction valeur absolue est définie sur R et dérivable sur R∗ de dérivée égale à
−1 sur R∗− et 1 sur R∗+ .
• La fonction valeur absolue est paire, strictement décroissante sur R− et strictement
croissante sur R+ .
8
La représentation graphique de la fonction valeur absolue est la suivante.
|x|
4
3
2
1
−4
−3
−2
−1
1
2
3
4
Fonction partie entière
Définition 26
Soit x un réel. La partie entière de x, notée bxc, est l’unique entier n vérifiant
n6x<n+1
Proposition 27
• La fonction partie entière est définie sur R et continue et dérivable sur R\Z de
dérivée nulle.
• La fonction partie entière est croissante.
La représentation graphique de la fonction partie entière est la suivante.
3
2
1
−4
−3
−2
−1
1
−1
−2
−3
9
2
3
4
Fonctions circulaires
Proposition 28
• La fonction cosinus, notée cos, est définie sur R, paire, 2π-périodique et dérivable
sur R avec cos0 = − sin.
• La fonction sinus, notée sin, est définie sur R, impaire, 2π-périodique et dérivable
sur R avec sin0 = cos.
[ π
π
• La fonction tangente, notée tan, est définie sur D =
− + kπ , + kπ ,
2
2
k∈Z
impaire, π-périodique et dérivable sur D avec
tan0 = 1 + tan2 =
1
cos2
Les fonctions cosinus et sinus sont « déphasées » de π/2.
1
cos x
−
−π
3π
2
−
π
2
π
2
−1
π
3π
2
sin x
La représentation de la fonction tangente est la suivante.
tan x
3
2
1
−
3π
2
−π
−
π
2
−1
π
2
π
3π
2
−2
−3
Il arrive fréquemment de connaître cos(x), sin(x) ou tan(x) et de vouloir en déduire le réel x
(en fait, les réels x, du fait de la périodicité des fonctions circulaires). Pour ce faire, on souhaite inverser les fonctions cosinus, sinus et tangente ; on définit donc les fonctions circulaires
réciproques Arccos, Arcsin et Arctan.
10
Fonctions circulaires réciproques
Définition 29
• La restriction de la fonction cosinus à [ 0 , π ] est une bijection strictement décroissante de [ 0 , π ] sur [ −1 , 1 ].
On note alors Arccos la fonction réciproque de cette restriction, qui est une bijection strictement décroissante de [ −1, 1 ] sur [0 , π ].
π π
• La restriction de la fonction sinus à − ,
est une bijection strictement crois2 2
π π
sante de − ,
sur [ −1 , 1 ].
2 2
On note alors Arcsin la fonction réciproque de cette restriction, qui est une bijecπ π
.
tion strictement croissante de [ −1 , 1 ] sur − ,
2 2
π π
• La restriction de la fonction tangente à − ,
est une bijection strictement
2 2
π π
sur R.
croissante de − ,
2 2
On note alors Arctan la fonction réciproque
de cette restriction, qui est une bijec
π π
.
tion strictement croissante de R sur − ,
2 2
En termes de résolution d’équations, les fonctions circulaires réciproques se caractérisent de
la façon suivante.
Proposition 30
Soit a ∈ [ −1 , 1 ] et b ∈ R.
• Arccos(a) est l’unique solution de l’équation cos(x) = a dans l’intervalle
[ 0 , π ]. π π
• Arcsin(a) est l’unique solution de l’équation sin(x) = a dans l’intervalle − ,
.
2 2
π π
• Arctan(b) est l’unique solution de l’équation tan(x) = b dans l’intervalle − ,
.
2 2
Remarque
Les équations cos(x) = a, sin(x) = a et tan(x) = b ont par contre une infinité
de solutions sur R. Bien sûr, si a < −1 ou a > 1, les équations cos(x) = a et sin(x) = a n’ont
aucune solution réelle.
11