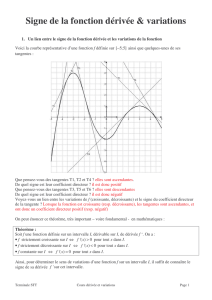
Dérivation : point de vue global

'Dérivation : point de vue global '
I Fonction dérivée
I.1 Fonction dérivée
Soit fune fonction définie et dérivable sur un intervalle I.
On a vu que pour a∈I, lim
h→∞
f(a+h)−f(a)
hexiste et on l’a appelé « nombre dérivé de fen a»et noté f0(a).
Définition 1
Soit fune fonction dérivable en tout point xd’un intervalle I, alors la fonction qui à xassocie f0(x) est appelée fonction
dérivée de fsur I. On la note f0.
I.2 Dérivées des fonctions usuelles
Ensemble de
Définition Fonction fDérivée f0Ensemble de
dérivabilité de f
Rx7→ k x 7→ 0R
Rx7→ x x 7→ 1R
Rx7→ x2x7→ 2xR
Rx7→ x3x7→ 3x2R
R+x7→ √x x 7→ 1
2√x
R∗+
R∗x7→ 1
xx7→ − 1
x2R∗
R∗+x7→ lnx x 7→ 1
xR∗+
Rx7→ exx7→ exR
II Opérations sur les fonctions dérivables
Fonction fDérivée f0
k.u(x)k.u0(x)
u(x) + v(x)u0(x) + v0(x)
u(x).v(x)u0(x).v(x) + u(x).v0(x)
u(x)
v(x)
u0(x).v(x)−u(x).v0(x)
(v(x))2
eu(x)u0(x)eu(x)
Si u(x)>0 ln(u(x)) u0(x)
u(x)
1

III Dérivée et sens de variation
III.1 Variations d’une fonction affine
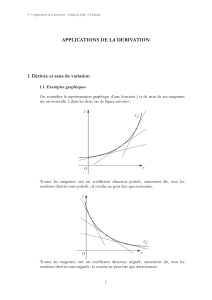
La tangente à une courbe en un point est une droite qui représente une fonction affine.
Si le coefficient directeur de la droite est positif, alors la fonction affine associée est croissante.
Si le coefficient directeur de la droite est négatif, alors la fonction affine associée est décroissante.
Interprétation graphique :
Sur la figure ci-dessous, toutes les tangentes à Cont
un coefficient directeur positif ; les nombres dérivés de
fsont positifs. Les tangentes « montent », et donc la
courbe Caussi : la fonction fest croissante.
0
Sur la figure ci-dessous, toutes les tangentes à Cont un
coefficient directeur négatif ; les nombres dérivés de f
sont négatifs. Les tangentes « descendent », et donc la
courbe Caussi : la fonction fest décroissante.
0
Attention, ces résultats ne sont que des conjectures et non pas des démonstrations.
Théorème 1 (admis)
Soit fune fonction dérivable sur un intervalle I.
– Si f0est strictement positive sur I, alors fest strictement croissante sur I.
– Si f0est strictement négative sur I, alors fest strictement décroissante sur I.
– Si f0est nulle sur I, alors fest constante sur I.
III.2 Tableau de variation
Pour bien visualiser ce résultat essentiel, nous adopterons un tableau de variation qui intégrera à la fois le signe de la
dérivée f0et le sens de variation de la fonction f.
Exemple 1
Soit fla fonction définie sur Rpar f(x) = x2−6x+ 1.
1. fest dérivable sur Ret pour x∈R, on a : f0(x) = 2x−6.
2. 2x−6>0 si et seulement si x > 3. On obtient donc le tableau suivant :
3. D’autre part f(3) = 32−6×3 + 1 = 9 −18 + 1 = −8.
On obtient donc le tableau suivant :
x−∞ 3 +∞
f0−0 +
f
+∞@@@R
−8
+∞
2