Fonctions de référence - Fonctions usuelles

1
Séquence 6 – MA20
Séquence 6
Fonctions de référence
Fonctions usuelles
Sommaire
1. Prérequis
2. Fonction carré et fonction inverse
3. Fonctions polynômes de degré 2 ; fonctions homographiques
4. Trigonométrie
5. Algorithmique
6. Synthèse de la séquence
7. Exercices d’approfondissement
© Cned – Académie en ligne

3
Séquence 6 – MA20
1Prérequis
Les séquences 1 et 3 du cours.
O
n rappelle en particulier les dé
fi
nitions suivantes
D
ire
q
ue
f
est
f
croissante sur
l’
interva
ll
e
I
si
g
ni
fi
e que pour tous réels
u
et
u
v
de
v
l
’intervalle I
,
s
i uv ≤, alors fu fv () ().≤
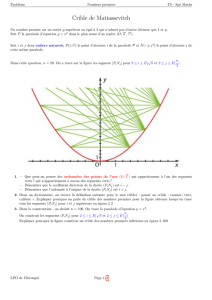
L
a courbe représentative d’une
fonction croissante sur l’intervalle I
« monte » lors
q
ue
x
décrit I.
x
P
ar exemple, on lit sur le dessin ci-
d
essous que
f
est cro
i
ssante sur
I
= [−2,5 ; 2]
Dire
q
ue
f
est
f
décroissante
s
u
r
l
’intervalle I si
g
ni
fi
e que pour tous
r
ée
l
s
u
et
u
v
de l’intervalle I,
v
si
uv ≤, alors fu fv () ().≥
L
a courbe représentative d’une
f
onction décroissante sur l’intervalle I
«
descend » lors
q
ue
x
décrit I.
x
P
ar exemple, on lit sur le dessin
ci-
d
essous que
f
est décroissante sur
f
I
= [−2,5 ; 2]
u
f(u)
v
f(v)
2-1-2
-1
-2
01
1
2
x
y
u
f(u)
v
f(v)
2
-1
-2
-1
-2
01
1
2
x
y
P
our tous rée
l
s
u
et
u
v
,
fu ()e
t
fv ()
sont rangés
d
ans
l
e même ordre
que
u
et
u
v
.
P
our tous rée
l
s
u
et
u
v
,
fu () e
t
fv ()
s
ont rangés
d
ans l’ordre contraire
de
e
u
et
u
v
.
AA
© Cned – Académie en ligne

4
Séquence 6 – MA20
Relations trigonométriques dans
le triangle rectangle
A
BC est un triang
l
e rectang
l
e en A.
cos ˆˆ;B= côté adjacent à B
hypoténuse
BA
BC
=
sinB = côté opposé à B
hypoténuse
CA
CB
ˆˆ;=
tanB = côté opposé à B
côté adjacent à B
ˆˆ
ˆ=AAC
AB .
S
i on connaît
l
a
l
ongueur
d
e
d
eux côtés
d’
un triang
l
e rectang
l
e, on peut à
l’
ai
d
e
d
’une calculatrice ré
g
lée en mode de
g
ré déterminer une valeur approchée des
a
n
g
les de ce trian
g
le
.
Par exemp
l
e, si on sait que AB = 4 cm et BC = 5 cm, on peut en
d
é
d
uire que :
cos ˆ,B=4
5=08
e
t on en déduit en effectuant
2
nde
cos
0.8 que ˆ B≈ 36,87°
BB
A
C
BA
C
B
© Cned – Académie en ligne

5
Séquence 6 – MA20
Activités
La caisse à gâcher
L
l
H
h
Dimensions de la caisse à gâcher : L
= 60 cm ;
L
l
= 40 cm ;
l
H
= 30 cm .
H
C
alculer
,
en litres
,
le volume total
V
t
de la caisse à gâcher.
t
C
a
l
cu
l
er
,
en
l
itres
,
l
e vo
l
ume
d’
eau
V
contenu dans la caisse à gâcher pour
V
u
ne
h
auteur
d’
eau
d
e 10 cm
p
uis
p
our une
h
auteur
d’
eau
d
e 20 cm. A-t-i
l
doub
l
é
?
E
xprimer le volume
V
(
en litres
)
en fonction de
la
h
auteu
r
d
’
eau
h
(
en cm
).
 a) Compléter le tableau de valeur ci-dessous
.
h
(cm)
h
0
4
8
1
2
1
6
20
2
4
28
30
V
(
V
h
)
h
h
AA
Activité 1Activité 1
2Fonction carré
et fonction inverse
© Cned – Académie en ligne

6
Séquence 6 – MA20
b)
T
racer
l
a cour
b
e représentative
d
u vo
l
ume
V
en fonction de la hauteur d’eau
V
h
.
x
yV
en litres
h en cm
36
32
28
24
20
16
12
8
4
04 8 12 16 20 24 28 32
Un rectangle d’aire constante.
L’
u
ni
té
c
h
o
i
s
i
e
est
l
e
c
m.
L
’
aire
d’
un rectang
l
e OABC est
d
e 8.
On note
x =OA e
t
y =OC .
 Ex
p
rimer
y
en fonction de
y
x
.
Rem
p
lir le tableau de valeurs suivant (résultats arrondis au centième si
nécessaire
).
f
désigne la fonction telle que
f
yfx =().
x
0,
5
0,
75
1
2
3
4
6
8
12
1
6
y
=
fx ()
Activité 2Activité 2
© Cned – Académie en ligne