Électrostatique - Page d`accueil

Électrostatique
E.1. Champ intérieur à un condensateur plan
Déterminer le champ électrique E et le potentiel électrique V créés par un plan infini, plan xOy,
chargé avec une densité surfacique de charge constante σ en tout point de l’espace.
On pose V(z = 0) = 0.
En déduire le champ E et le potentiel V électrostatiques créés par deux plans infinis, placés
respectivement en z = e et z = – e et chargés avec des densités surfaciques – σ et σ.
On pose V(z = 0) = 0.
En modélisant un condensateur plan par l’association de deux disques de même axe Oz, de
même aire S = π.a
2
, distants de e avec a >> e, déterminer l’expression de sa capacité C en
fonction de S, ε
0
et e.
E.2.
Déterminer les expressions en tout point M de l’espace du champ E et du potentiel V
électrostatiques créés par une boule, de centre O et de rayon a, chargée avec la densité
volumique : ρ(u) = ρ
0
(1 –
2
2
u
a
) pour u ≤ a et ρ(u) = 0 pour u > a avec u = OP.
E.3.
Déterminer la différence de potentiel entre deux fils conducteurs cylindriques, de rayons R et
R’, dont les axes parallèles sont distants de d (d >> R et R’), portants respectivement les
densités de charges linéiques λ et – λ.
En déduire la capacité linéique de cette ligne bifilaire. Cas particulier où R = R’.
E.4. Modèle de Thomson
Supposons qu’un atome d’hydrogène soit constitué d’un électron ponctuel noté N, de masse m
et de charge q
N
= − e évoluant dans nuage sphérique, de centre P, de rayon a et dont la charge
totale q
P
= + e est répartie dans cette sphère avec une densité volumique de charge ρ
uniforme. L’électron peut se mouvoir sans frottement à l’intérieur du nuage. La masse M de ce
nuage étant très supérieure à celle de l’électron, on peut supposer P fixe dans le référentiel
galiléen d’observation ; N est mobile et repéré par son vecteur position r = PN.
• Déterminer le champ électrostatique E
+
(N) créé par le nuage positif au niveau de
l’électron, en fonction de e, a, ε
0
(permittivité du vide) et r.
On suppose que l’électron reste à l’intérieur du nuage.
• Montrer que le mouvement de l’électron dans ce champ est associé à une fréquence f
0
que l’on exprimera en fonction de m, e, a et ε
0
.

E.5. Potentiel de Yukawa CCP 2015
On considère une distribution de charges de symétrie sphérique autour d'un point O origine du
repère. En un point M tel que OM = r, le potentiel électrostatique est donné par :
V(M) = V(r) =
r
a
0
q
e
4 r
πε
−
q et a sont des constantes positives respectivement homogènes à une charge électrique et à
une longueur.
1. Déterminer l’expression du champ électrostatique E(M) en tout point de l’espace.
Donner des équivalents au champ E lorsque r tend vers 0 et vers l’infini.
Que peut-on en déduire ?
2. Calculer Q(r) la charge intérieure à une sphère de rayon r et de centre O.
Calculer les limites de la charge Q(r) lorsque r tend vers 0 et vers l’infini.
Retrouver les conclusions précédentes.
3. Calculer la charge volumique ρ(r) en M ainsi que la charge diffuse Q
diff
contenue dans une
sphère de centre O et de rayon r.
E.6. Tranche de charges (incontournables p159)
On considère une distribution volumique (D) de charges ρ uniforme, d’extension infinie,
comprise entre deux plans z = –
a
2
et z =
a
2
dans le repère (O, u
x
, u
y
, u
z
).
1. Calculer le champ et le potentiel électrostatiques en tout point de l’espace. On pose V(0) = 0.
2. Étudier le cas où a tend vers 0.
E.7. Distribution entre deux sphères concentriques (incontournables p167)
On considère une charge q négative répartie en volume entre deux sphères concentriques de
rayons R
1
et R
2
. On appelle ρ(r) la densité volumique de charges entre R
1
et R
2
. Le champ
électrostatique se met sous la forme E(M) = a(r – R
1
).u
r
pour R
1
≤ r ≤ R
2
avec a une constante.
1. Déterminer la densité volumique de charge ρ(r) en fonction de a, r, R
1
et ε
0
.
2. Déterminer a en fonction de q, ε
0
, R
1
et R
2
.
3. Déterminer le champ électrostatique en tout point de l’espace.
4. En déduire le potentiel électrostatique en tout point de l’espace. On pose V(∞) = 0.
E.8. Capacité d’un câble coaxial CCP 2015
Un câble coaxial est formé d’un conducteur cylindrique plein, de rayon R
1
, de charge Q, de
longueur h, d’axe Oz, de potentiel V
1
> 0, entouré d’un conducteur cylindrique creux, de rayon
intérieur R
2
, de charge – Q, de potentiel V
2
= 0. Le vide sépare les deux conducteurs.
On néglige les effets de bord. On pose U = V
1
– V
2
. La capacité C du câble coaxial est définie
par Q = CU.
1. Déterminer le champ électrostatique dans l’espace défini par R
1
< r < R
2
.
2. En déduire l’expression du potentiel électrostatique dans l’espace défini par R
1
< r < R
2
.
3. Donner l’expression de la capacité C du câble en fonction de h, R
1
, R
2
et ε
0
.

E.9. Champ de module constant dans une sphère
On considère une répartition volumique de charge électrique présentant la symétrie sphérique,
contenue à l’intérieur d’une sphère de rayon R et de centre O.
a. Déterminer cette répartition caractérisée par ρ(r) pour que le champ électrique ait un module
constant à l’intérieur de la sphère.
b. Déterminer la charge totale Q de la sphère et le champ électrostatique à l’extérieur de la
sphère.
E.10. Champ dans une cavité CCP 2015
On considère sur le repère orthonormé (O, e
x
, e
y
, e
z
) une sphère de centre O et de rayon R, de
densité de charge ρ ≥ 0, dans laquelle on creuse une cavité sphérique vide de charge, de
centre O' et de rayon R' tel que OO’ = d.e
y
.
a. Exprimer le champ E(M) en tout point M de la cavité en fonction de ρ, ε
0
et d.
b. Quelle est la particularité de ce champ ?
E.11. Sphères chargées ENSEA 2015
1. Une sphère S de rayon R et de centre O est chargée en surface et portée au potentiel V.
Déterminer la charge totale Q de la sphère et sa densité surfacique de charge σ en fonction
de R et de V.
2. Deux sphères de rayon R
1
et R
2
(R
1
< R
2
) concentriques de centre O d’épaisseur
négligeables chargées en surface et portées aux potentiels V
1
et V
2
.
a. Déterminer le champ électrostatique E en tout point de l’espace.
b. Exprimer les densités surfaciques de charge σ
1
et σ
2
en fonction de des données.
c. On fixe V
2
= 0. Étudier le potentiel dans tout l‘espace
d. Donner la capacité C du condensateur formé par les deux sphères.
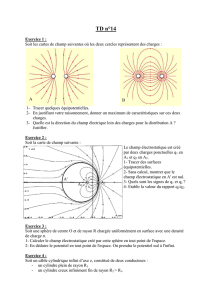
E.12. Lignes de champ et équipotentielles
Considérons trois charges identiques (q > 0) au sommet d’un triangle équilatéral de côté a.
a. Trouver un point évident de champ nul.
Quel est la valeur du potentiel en ce point ? On prendra le potentiel nul à l’infini.

b. La simulation suivante, représentant les lignes de champ et les équipotentielles, montre qu’il
existe trois autres points de champ nul. Mesurer leur position et donner la valeur du potentiel
en ces points.
Dipôle électrostatique
D.E.1. Le quadrupôle électrostatique
Déterminer l’expression du potentiel électrostatique V créé par un ensemble de trois charges
alignées, 2q en O, origine de l’espace, – q en A(+a, 0, 0) et en B(– a, 0, 0), en un point M de
l’espace situé à une distance r de O (r >> a). On pose V(r = ∝) = 0.
On rappelle le développement limité à l’ordre 2 en 0 :
1
1 x+
= 1 –
x
2
+
2
3x
8 + O(x
3
)
En déduire l’expression du champ électrique E .
Tracer à la calculatrice sur le même graphe les lignes de champ et les équipotentielles.
Connaissez-vous des exemples de quadrupôles ?
On pose r = OM , r
A
= AM , r
B
= BM , θ = ( OA , OM ).
D.E.2. actions exercées par un fil infini chargé sur un dipôle
Déterminer les actions mécaniques exercées par le champ d’un fil rectiligne infini portant la
charge linéique uniforme λ sur un dipôle placé en M dans un plan perpendiculaire au fil.
On note α l’angle entre les vecteurs e
r
et p .
D.E.3. Dipôles en interaction
Soit un ensemble infini de dipôles p , p = p. u
x
, p > 0, équidistants de a le long de l’axe Ox.
Calculer la différence d’énergie électrostatique entre les états (II) et (I) définis par :
• État (I) : Tous les dipôles (i) sont définis par p
i
= p .
• État (II) : Tous les dipôles (i) placés à une abscisse négative sont définis par p
i
= p et tous
les dipôles (j) placés à une abscisse positive sont définis par p
j
= – p .