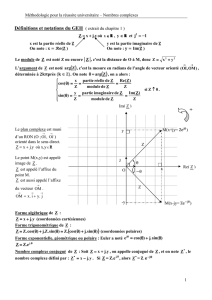
Nombre complexe et argument

Terminale S/Nombre complexe et argument
1. Rappel de trigonométrie :
Exercice 3792
Soit ¸un nombre réel. Simplifier les écritures suivantes :
a. cos ı
2+¸b. sin ¸+3·ı
c. cos ¸−ı
2d. sin ı 2−¸
Exercice 3793
Résoudre les équations suivantes :
a. sin x+ı
4=√3 2b. cos 2x+ı 3=2 2
Exercice 5947
1. En remarquant l’égalité ı
12=ı 3−ı 4, déterminer les va-
leurs de cos ı
12 et sin ı 12.
2. Déterminer les valeurs de : cos 7ı
12 ;sin 7ı 12
Exercice 3794
1. a. Développer l’expression : sin x+ı
4.
b. Résoudre l’équation : sin x+ cos x= 1
2. a. Développer l’expression : cos x+ı
3.
b. Résoudre l’équation : cos x−3·sin x= 1
2. Forme trigonométrique :
Exercice 3795
On considère le plan
muni d’un repère
O;−→
u;−→ vorthormé
direct représenté ci-
dessous :
Le cercle Cde centre O
et de rayon 2est repré-
senté en pointillé ; les
points Cet Dappar-
tiennent au cercle C.
-2 -1 01 2
-2
-1
1
2
~u
~v
A
B
C
D
E
1. Déterminer les modules et les arguments des affixes des
points A,B,C,Det E.
2. Placer les points Fet Gd’affixes respectives zet z′vé-
rifiant :
|z|=2
arg z=−3ı
4
;
|z′|= 2
arg z′=−ı
2
Exercice 5952
Donner l’écriture trigonométrique des nombres complexes :
a. z1= 2·cos ı
4−i·sin ı 4
b. z2=−3·cos 2ı
3+i·sin 2ı 3
c. z3= cos ı
6+i·sin −ı 6
d. z4= 2·cos ı
4+i·sin 3ı 4
3. Forme trigonométrique et opérations :
Exercice 5951
On considère deux nombres complexes zet z′de modules
respectifs ret r′et d’arguments respectifs „et „′.
1. Donner l’écriture trigonométrique des nombres com-
plexes zet z′.
2. Montrer que le nombre complexe z·z′est un nombre com-
plexe de module (r·r′)et d’argument („+„′).
3. Montrer que le nombre complexe z
z′est un nombre com-
plexe de module r
r′et d’argument („−„′).
Terminale S - Nombre complexe et argument - http://chingatome.net

4. Forme trigonométrique et géométrie :
Exercice 5359
On considère le plan muni du repère (O;−→ u;−→ vet les quatre
points A,B,Cet Dd’affixes respectives :
zA=−2+i;zB=−3·i;zC=3−2·i;zD=3+2·i
1. a. Donner l’écriture algébrique du nombre complexe Z
défini par le quotient :
Z=zC−zA
zD−zB
b. En déduire l’écriture trigonométrique du complexe Z.
2. a. Justifier que le quadrilatère ABCD a ses diagonales
perpendiculaires et de même longueur.
b. Le quadrilatère ABCD est-il un losange ?
Exercice 5360
Dans le plan muni d’un repère O;−→ u;−→ v, on considère les
trois points A,Bet Cd’affixes respectives :
zA=−2 + i;zB=−3·i;zC= 6 + 5·i
1. Placer ces trois points dans le repère ci-dessous :
-3 -2 -1 2 3 4 5 6 7
I
-4
-3
-2
-1
2
3
4
5
J
O
2. Démontrer que le triangle ABC est un triangle rectangle.
3. On considère le point Dd’affixe zDoù : zD=4−i
a. Donner l’écriture algébrique du nombre complexe Z
définie par :
Z=zB−zA
zD−zA
b. Justifier que la demi-droite [AD)est la bissectrice de
l’angle Ä−−→ AB ;−→ ACä.
5. Forme exponentielles :
Exercice 3848
Déterminer l’écriture exponentielle des nombres complexes
suivants :
a. z1= 5 b. z2=−3c. z3=−3·i
d. z4=−3+3·ie. z5=−23−2·if. z6=3−3·i
Exercice 5366
On considère les deux nombres complexes donnés ci-dessous :
z1=3·ei·π
3;z2=6·e−i·π 6
Déterminer une expression simplifiée des calculs suivants :
a. z1·z2b. z1
z2
c. z1+z2
Exercice 3831
1. Soit zun nombre complexe admettant la forme exponen-
tielle :
z=r·ei·θoù r∈R+,„∈R
Déterminer la forme exponentielle des nombres com-
plexes suivants :
a. zb. −z
2. a. Justifier l’égalité suivante :
3·ei·2π
3=−3·e−i·π 3
b. En déduire l’écriture exponentielle de :
2·e−i·π
3+ 3·ei·2π 3
Exercice 4253
Dans C, on considère les deux nombres complexes suivants :
zA= 1 −i;zB= 2 + 3 + i
1. Déterminer le module et un argument de zA.
2. Ecrire zB
zA
sous écriture algébrique.
3. Montrer que : zB
zA
=(1+3)·ei·π
3
4. En déduire l’écriture exponentielle de zB.
Exercice 3798
1. Déterminer l’écriture algébrique du nombre complexe z
défini par z=1−i
1+i
2. a. Donner l’écriture exponentielle des deux nombres
complexes suivants : z1=1−i;z2= 1+i
b. En déduire l’écriture exponentielle du nombre com-
plexe z.
3. Déterminer l’écriture exponentielle du nombre complexe
z3définie par : z3=1+i
1−√3·i
Terminale S - Nombre complexe et argument - http://chingatome.net

Exercice 3827
On considère dans Cles nombres complexes z1et z2de mo-
dule 1et d’arguments respectifs ¸et ˛. Montrer que :
z1+z22
z1·z2
est un réel positif ou nul.
Exercice 6380
On considère la suite de nombres complexes zndéfinie par ;
z0=3−i;zn+1 =1 + i·znpourt tout n∈N
1. Déterminer la forme algébrique de z1.
2. Déterminer la forme exponentielle de z0et 1+i.
En déduire la forme exponentielle de z1.
3. Déduire des questions précédentes la valeur exacte de
cos ı
12
6. Forme exponentielle et mesure principale de l’argument :
Exercice 5381
On considère les deux nombres complexes suivants donnés
sous leur forme trigonométrique :
z1= 2·ei·2π
3;z2= 3·ei·3π 4
Donner l’écriture exponentielle des expressions suivantes :
a. z1·z2b. z12·z2c. z2
z12
Exercice 3829
1. a. Soit z1le nombre complexe admettant pour écriture
algébrique : z1=−2·3+2·i
Déterminer l’écrituer exponentielle de ce nombre.
b. Soit z2le nombre complexe vérifiant :
|z2|=2;arg(z2) = 3
4·ı
Déterminer l’écriture algébrique du complexe z2
2. Déterminer, à votre convenance, soit l’écriture algé-
brique, soit l’écriture exponentielle des nombres com-
plexes suivants :
a. z1·z2b. z1+z2
Exercice 3810
1. Résoudre dans l’ensemble des nombres complexes l’équa-
tion :
z2−2z+ 4 = 0
Les solutions seront notées zet z′,z′désignant la solu-
tion dont la partie imaginaire est positive.
Donner l’écriture algébrique puis l’écriture exponentielle
des solutions de cette équation.
2. Donner l’écriture exponentielle exacte du nombre com-
plexe z′2 004, puis son écriture algébrique.
Exercice 5325
On considère le nombre complexe : a=−3+i2011.
Indiquer si l’affirmation suivante est vraie ou fausse en justi-
fiant la réponse :
“Le nombre complexe aest un nombre imaginaire pur.”
Exercice 6081
Le plan complexe est rapporté à un repère orthonormal direct
O;−→
u;−→ v. On considère l’application zde Cdans Cdéfinie
par :
f:z7−→z2.
On considère le complexe : a=2−i·2
1. Exprimer asous écriture exponentielle.
2. En déduire les nombres complexes antécédents du
nombre apar f.
7. Géométrie et argument :
Exercice 4105
Dans le plan complexe muni du repère orthonormal
O;−→
u;−→ v, on considère les points Met M′d’affixes res-
pectives zet z′. On pose :
z=x+i·y;z′=x′+i·y′
où x,x′,y,y′sont des nombres réels.
On rappelle que zdésigne le conjugué de zet que |z|désigne
le module de z.
1. Exprimer le complexe z·z′en fonction de x,x′,y,y′.
2. a. Montrer que les vecteurs −−→ OM et −−−→ OM′sont orthogo-
naux si, et seulement si, Rez′·z=0.
b. Montrer que les points O,Met M′sont alignés si, et
seulement si, Im(z′·z)=0
8. Géométrie et complexes :
Exercice 5380
Décrire avec l’écriture algébrique ou l’écriture exponentielle
des parties du plan représentées ci-dessous :
~u
~v
2
~u
~v
2
~u
~v
π
6
Terminale S - Nombre complexe et argument - http://chingatome.net

Exercice 3796
On considère le plan muni d’un repère O;−→ u;−→ vortho-
normé direct. Décrire l’ensemble des points Mdu plan dont
l’affixe zvérifie les conditions suivantes :
a. |z|= 1 b. |z|⩽3c. 1⩽|z|⩽2
d. arg(z) = ı
2e. 
arg(z) =ı
4
Exercice 4320
Le plan complexe est muni d’un repère orthonormé direct
O;−→
u;−→ v. On prendra 2cm pour unité graphique. On ap-
pelle Jle point d’affixe i.
1. On considère les points A,B,C,Hd’affixes respectives :
a=−3−i;b=−2+4·i;c= 3−i;h=−2.
Placer ces points sur une figure, qui sera complétée au
fur et à mesure de l’exercice.
2. Montrer que Jest le centre du cercle Ccirconscrit au
triangle ABC. Préciser le rayon du cercle C.
3. Donner l’écriture algébrique du nombre complexe b−c
h−a.
En déduire que les droites (AH)et (BC)sont perpendi-
culaires.
Exercice 3854
Dans le plan complexe muni d’un repère orthonormal direct
O;−→
u;−→ v, on considère les points A,B,C,Dd’affixes res-
pectives :
zA=−3−i;zB= 1 −i·3
zC=3 + i;zD=−1 + i·3
1. Donner le module et un argument de chacun des quatre
nombres complexes zA,zB,zCet zD.
2. Construire à la règle et au compas les points A,B,Cet
D(on prendra pour unité graphique 2cm).
3. Déterminer le milieu du segment [AC], celui du segment
[BD]. Calculer le quotient zB
zA
. En déduire la nature du
quadrilatère ABCD.
Exercice 4314
Le plan complexe est rapporté à un repère orthonormal direct
O;−→
u;−→ v
1. Résoudre dans Cl’équation : 2·z2−6·z+9=0
On désigne par P,Qet Rles points d’affixes respectives :
zP=3
2·1 + i;zQ=3 2·(1 −i);zR=−2·i·3
2. On note Sle symétrique du point Rpar rapport au point
Q. Vérifier que l’affixe zSdu point Sest :
zS= 3 + i·2·3−3
9. Transformations du plan :
Exercice 6020
A tout nombre complexe ztel que z̸=2, on associe le nombre
complexe z′définie par :
z′=z+ 3
z−1
1. On note x+i·y, où x∈Ret y∈R, l’écriture algébrique du
nombre complexe z.
Donner l’écriture algébrique du nombre z′, associé à z,
en fonction de xet de y.
2. a. On considère l’équation cartésienne :
(E):x2+y2+ 2x−3 = 0
Justifier que, dans le plan, l’ensemble des solutions de
(E)est le cercle Cde centre (−1;0)et de rayon 2.
b. Déterminer l’ensemble des nombres complexes ztels
que le nombre complexe z′associé soit un imaginaire
pur.
Exercice 4078
Dans le plan complexe rapporté au repère orthonormal direct
O;−→
u;−→ v. On note Ale point d’affixe i.
Pour tout point Md’affixe ztel que z̸=i, on définit le point
M′dont l’affixe z′est défini par :
z′=1
3·(z−i)
1. Etablir la proposition suivante :
Si Mest un point du cercle de centre Ade rayon
r, alors M′est un point du cercle de centre Ode
rayon 1
3·r.
2. Démontrer que : arg(z′) = −Ä−→ u;−−→ AMä
Exercice 4099
Dans le plan muni d’un repère orthonormal O;−→ u;−→ v, on
considère les points Aet Bd’affixes respectives 2et (−2).
On définit l’application fqui à tout point Md’affixe zet
différent de Aassocie le point M′d’affixe :
z′=z·(z−2)
z−2
1. Montrer que pour tout nombre complexe z, le nombre
complexe (z−2)(z−2) est réel.
2. En déduire que pour tout nombre complexe distinct de
2,z′+2
z−2est réel.
3. Montrer, pour tout point Mdu plan, que les droites
(AM)et (BM ′)sont parallèles.
10. Suites :
Terminale S - Nombre complexe et argument - http://chingatome.net

Exercice 3875
On considère le plan muni d’un repère orthonormal
O;−→
u;−→ v. Soit Aet Bles points d’affixes respectives :
zA=i;zB= 2 + 2·i
1. Soit Iun point du plan dont l’affixe zIvaut :
zI=−4 + 23
2·i
Montrer que le point Iappartient à la médiatrice du seg-
ment [AB].
2. Soit Mun point du plan d’affixe (2+i).
Montrer que le point Mappartient au cercle de diamètre
[AB].
Exercice 6384
Le plan complexe est muni d’un repère orthonormé
O;−→
u;−→ v.
Pour tout entier naturel n, on note Anle point d’affixe zn
défini par :
z0= 1 ;zn+1 =3
4+√3 4·i·zn
1. Déterminer les affixes des poitns A1et A2.
2. Démontrer que le triangle OAnAn+1 est rectangle en
An+1.
3. On admet que, pour tout entier naturel n:
zn=
zn ·ei·n·π
6
Placer les point A0,A1,A2,A3et A4dans le repère
ci-dessous :
I
J
O
Exercice 6381
On considère la suite de nombres complexes zndéfinie par :
z0=3−i;zn+1 =1 + i·zn
Pour tout entier naturel n, on pose : un=
zn .
1. Calculer u0.
2. Démontrer que unest la suite géométrique de raison
2et de premier terme 2.
3. Pour tout entier naturel n, exprimer unen fonction de
n.
4. Déterminer la limite de la suite un.
Exercice 6382
On considère la suite znde nombres complexes définies par :
z0= 4 ;zn+1 =1 + i
2·znpour tout n∈N
Dans le plan muni d’un repère orthonormé direct d’origine O,
on note Anle point image du nombre complexe zn.
-2 -1 2 3 4
I
-1
2
3
J
O
1. a. Calculer z1,z2et z3.
b. Placer les points A1,A2et A3dans le repère ci-dessous.
2. On note ‘nla longueur de la ligne brisée qui relie le point
A0au point Anen passant sucessivement par les points
A1,A2,A3. . .
Ainsi : ‘n=
n
k=1
Ak−1Ak=A0A1+A1A2+···+An−1An
a. Etablir la relation ci-dessous pour tout entier naturel
nnon-nul :
An−1An=
zn
b. A l’aide d’un raisonnement par récurrence, établir
l’égalité suivante pour tout entier naturel nnon-nul :
An−1An= 22·2
2n−1
c. Donner une expression de ‘nen fonction de n.
d. Déterminer la limite éventuelle de la suite ‘n.
Terminale S - Nombre complexe et argument - http://chingatome.net