chap-3-systemes-spheriques

Systèmes sphériques
____________________________________________________________________________________
1
Chap. 3
Systèmes sphériques
I. Dioptres sphériques : .......................................................................................................................... 2
I.1. Définition et notations : .............................................................................................................. 2
I.2. Image d'un point : ........................................................................................................................ 2
I.3. Relation de conjugaison avec origine au sommet : ................................................................ 3
I.4. Foyers d'un dioptre sphérique : ............................................................................................... 5
I.5. Construction de l'image d'un objet transversal : ................................................................. 6
I.6. Grandissement transverse : ....................................................................................................... 7
II. Miroirs sphériques : .......................................................................................................................... 7
II.1. Définition et notations :............................................................................................................ 7
II.2. Relation de conjugaison avec origine au sommet : .............................................................. 8
II.3. Foyers d'un miroir sphérique : ................................................................................................ 8
II.3. Construction de l'image d'un objet transversal : ............................................................... 8
III. Les lentilles : ..................................................................................................................................... 9
III.1. Les lentilles épaisses : ............................................................................................................. 9
III.1.1. Définition : .......................................................................................................................... 9
III.1.2. Position des foyers : ...................................................................................................... 10
III.1.3. Application à une sphère transparente : ................................................................... 11
III.2. Les lentilles minces : ............................................................................................................. 12
III.2.1. Définition et caractéristiques : .................................................................................. 12
III.2.2. Exemples de lentilles minces : .................................................................................... 12
III.2.3. Relation de conjugaison avec origine au centre : .................................................... 13
III.4. Foyers d'une lentille mince : ............................................................................................... 14
III.5. Construction d'une image : .................................................................................................. 14
IV. Quelques applications des lentilles: ............................................................................................ 15
IV.3.1. Loupe de Coddington : ..................................................................................................... 15

Systèmes sphériques
____________________________________________________________________________________
2
Chap. 3
SYSTEMES SPHERIQUES
Dioptres sphériques – Miroirs sphériques – Lentilles
I. Dioptres sphériques :
I.1. Définition et notations :
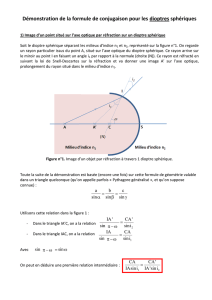
Un dioptre sphérique sépare deux milieux d'indice différents n1 et n2, et possède un rayon de
courbure R (Figure 1). Remarquons que le dioptre plan est un dioptre sphérique dont le rayon de
courbure est infini.
Figure 1
C centre du dioptre
S sommet du dioptre
R = rayon de courbure. R, compte tenu de
sa définition, peut être positif ou négatif.
(Cx) axe principal ou axe optique
I.2. Image d'un point :
Figure 2
Soit un point A de l'axe principal. Pour construire l'image A' de A, prenons un rayon issu de
A, frappant le dioptre en I (Figure 2). Dans l'exemple donné, n1 < n2. Si l'on considère un élément

Systèmes sphériques
____________________________________________________________________________________
3
infinitésimal du dioptre autour de I, cet élément peut être considéré comme plan. La loi de
Descartes indique que le rayon réfracté se rapprochera de la normale. Le rayon réfracté semble
provenir d'un point A' de l'axe (Cx). A' est l'image de A par le dioptre, puisqu'un rayon provenant
de A et passant par S émerge sans être dévié. Notons que A' est plus proche de S que A.
Figure 3
Dans le cas présenté ci-dessus, n1 > n2. L'image A' de A, toujours virtuelle, est repoussée vers
l'avant.
I.3. Relation de conjugaison avec origine au sommet :
AI
B
Ca
cb
Figure 4
Dans ce paragraphe, nous allons déterminer une relation entre la position de l'objet et de
l'image par rapport au point S. En préliminaire, nous allons démontrer une relation utile dans un
triangle quelconque (Figure 4) :
A
b
IC
Aˆ sin
ˆ
sin 
a
IC
B
ˆ
sin

Systèmes sphériques
____________________________________________________________________________________
4
donc
B
b
A
a
ˆ
sin
ˆ
sin 
De même, en appliquant cette méthode à l'angle
C
ˆ
, nous obtenons la relation générale
suivante :
C
c
B
b
A
a
ˆ
sin
ˆ
sin
ˆ
sin 
Dans le triangle (CIA1) (Figure 5) :
1
111 sinsinsin i
CAIAIA 
Dans le triangle (CIA1) :
2
222 sinsinsin i
CAIAIA 
Figure 5
2
2
2
1
1
1sinsinsin i
CA IA
i
CA IA 
de plus
2211 sinsin inin 
d'où :
CAn IA CAn IA
22
2
11
1
Cette relation, qui a été démontrée en utilisant les distances est à appliquer en fait sur les
mesures algébriques :

Systèmes sphériques
____________________________________________________________________________________
5
CAn
IA
CAn
IA
22
2
11
1
Dans les conditions de Gauss, c'est à dire pour des angles incidents très inférieurs à 1, I est
proche de S :
CAn
SA
CAn
SA
22
2
11
1
11 SACSCA 
de même
22 SACSCA 
2
22
1
11
2
21
1
11 SA
SACSn
SA
SACSn
SA
CAn
SA
CAn
2
2
1
111 SA
SC
n
SA
SC
n
2
22
1
11 SA
SC
nn
SA
SC
nn 
soit, en divisant les deux membres par
SC
:
SC
nn
SA
n
SA
n21
2
2
1
1
Cette relation est appelée relation de conjugaison avec origine au sommet.
I.4. Foyers d'un dioptre sphérique :
Le foyer image F' d'un système optique quelconque est l'image d'un objet situé à l'infini. De
la même manière, le foyer objet F est le lieu d'occupation d'un objet dont l'image est à l'infini.
A1 à l'infini donc A2 en F'. La relation de conjugaison devient :
SC
nn
SF
n212 '
d'où