Figures usuelles

OO
AB
R
D
C
Chapitre 5 FIGURES USUELLES
I. Cercle
1) Définition
Un cercle (C) de centre O est formé de tous les points situés à la même distance du point O.
Cette distance commune est appelée le rayon du cercle.
Exemple :
Le cercle de centre O et de rayon 2,5 cm est formé de tous les points situés à 2,5 cm du point O.
2) Vocabulaire
Prendre OA = 3 cm
Les points A, B, C, D, R appartiennent au cercle ci-dessus.
 Le segment [OR] est un rayon.
 Le segment [AB] est un diamètre.
 Les points A et B sont diamétralement opposés.
 Le segment vert d’extrémités C et D [CD] est une corde.
 La portion de cercle rouge est un arc de cercle. On le note CD .
Attention :
Le rayon du cercle est la distance r.
Ici le rayon du cercle est égal à 3 cm.
Un rayon du cercle est un segment ayant pour extrémités le centre du cercle et un point du cercle.
Les segments [OA], [OR], [OB] sont des rayons du cercle.
O
M
(C)

II.Polygone, triangle
1) Polygone
Définition
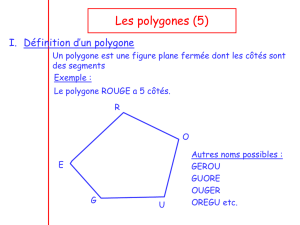
Un polygone est une figure fermée dont les côtés sont des segments.
Exemple :
Ce polygone se nomme ATIPU ou ITAUP ou TAUPI.
2) Triangle
Définition
Un triangle est un polygone à trois côtés.
a) Triangle rectangle
Un triangle rectangle est un triangle qui a un angle droit.
Le côté opposé à l’angle droit est appelé hypoténuse.
Exemple :
Le triangle ABC a un angle droit en A :
C’est un triangle rectangle en A.
b) Triangle isocèle
Un triangle isocèle est un triangle qui a deux côtés de même longueur.
Exemple :
AB = BC
Le triangle ABC est isocèle en B.
c) Triangle équilatéral
Un triangle équilatéral est un triangle qui a trois côtés de même longueur.
Exemple :
EF = GF = GE
Le triangle EFG est équilatéral.
 Remarque
Le triangle EFG est isocèle en E, isocèle en F et isocèle en G.
On dit quelquefois qu’un triangle est quelconque pour indiquer qu’il n’est ni rectangle ni isocèle.
G
F
E
B
A
C
[AC] est la base
Sommet principal
I
T
A
Ü
P
C
B
A
hypoténuse

III.Quadrilatères
1) Quadrilatère
Définition
Un quadrilatère est un polygone à quatre côtés.
Exemple :
Attention : l’ordre des points est très important pour nommer un quadrilatère.
Le quadrilatère ci-dessus peut se nommer ABCD, ou ………., ou ………., mais pas ……….
2) Rectangle
Un rectangle est un quadrilatère qui a quatre angles droits.
Le quadrilatère EFGH a 4 angles droits : c’est un rectangle.
3) Losange
Définition
Un losange est un quadrilatère qui a quatre côtés de même longueur.
Le quadrilatère RSTU est un losange car :
RS = ST = TU = UR
4) Carré
Un carré est un quadrilatère qui a quatre angles droits et quatre côtés de même longueur.
Le quadrilatère IJKL a 4 angles droits
et 4 côtés de même longueur : c’est un carré.
Un carré est à la fois un rectangle et un losange.
5) Parallélogramme
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
Le quadrilatère ABCD est un parallélogramme car
ses côtés opposés sont parallèles : (AB) // (DC) et (AD) // (BC).
U
R
S
T
C
B
A
D
K
I
L
J
E
G
F
H
B
D
C
A